◆静岡県 ヨッシー さんからの解答。
【問題1】
8個の玉から3個を選ぶ組み合わせは
8C3=56(通り)
8個の玉を重い順にABCDEFGHとします。
(1)3個を選ぶとき、必ずAを選ぶと考えると、
7C2=21(通り)・・・残り2個の選び方
| その確率は | 21 56 | = | 3 8 |
(2)3個を選ぶとき、必ずA、Bを選ぶと考えると、
6C1=6(通り)・・・残り1個の選び方
| その確率は | 6 56 | = | 3 28 |
| (3)同様にして、 | 1 56 |
●3個の玉で重さが1番であった玉が8個の玉で2番である確率
Bは必ず取り、C〜Hの6個から2個を取る選び方なので、
6C2=15(通り)
| 確率は | 15 56 |
●3番である確率
Cは必ず取り、D〜Hの5個から2個を取る選び方なので、
5C2=10(通り)
| 確率は | 10 56 | = | 5 28 |
以下同様に
●4番である確率
| 4C2 56 | = | 6 56 | = | 3 28 |
●5番である確率
| 3C2 56 | = | 3 56 |
●6番である確率
| 2C2 56 | = | 1 56 |
【問題2】
●R個の玉で重さが1番〜p番を占めたp個の玉が、N個の玉でも同じ順位を占める確率
※上の文は「p個の玉のみが」ではないものとして、解きます。
N個の玉からR個を選ぶ組み合わせは、
NCR 通り
N個の玉を重い順にA1,A2,A3,A4,・・・AN とします。
R個の玉を選ぶとき、A1〜Ap は必ず選び、
残りR−p個を Ap+1〜AN のN−p個から選ぶと考えると、その組み合わせは、
N-pCR-p (通り)
| 確率は、 | N-pCR-p NCR |
●R個の玉で重さが1番であった玉が、N個の玉でq番である確率
Aq は必ず取り、Aq+1〜AN のN−q個からR−1個を取ると考えると、その組み合わせは
N-qCR-1 (通り)
| 確率は、 | N-qCR-1 NCR |
◆出題者のコメント。
【問題1】【問題2】とも、みごと正解です。
必要にして十分な模範解答だと思います。
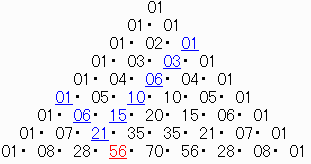
パスカルの三角形で見てみると以下になります。
【問題1】を例にしています。

以下は、ヨッシー さんの模範解答を参照してください。
上の 56(=NCR) が求める確率の分母になります。
21(=N-1CR-1) から左上に 21,06,01 ですが、これが、3個での1番まで,2番まで,3番までが、8個でも同順位になるそれぞれの確率の分子になります。
21(=N-1CR-1) から右上に 21,15,10,06,03,01 ですが、これが、3個での1番が8個で1番〜6番になるそれぞれの確率の分子になります。
なお、パスカルの三角形の1番上の 01 は 0C0 ですが、
R=1 やR=N の時に使用します。
◆静岡県 ヨッシー さんからの解答。
【問題2−2】
N個の玉からR個を選ぶ組み合わせは、
NCR 通り。
N個の玉を重い順にA1,A2,A3,A4,・・・AN とします。
●R個の玉で重さがp番であった玉が、N個の玉でq番である確率
Aq は必ず取り、A1〜Aq-1 のq−1個から、p−1個取り、
Aq+1〜AN のN−q個からR−p個を取ると考えると、その組み合わせは
q-1Cp-1・N-qCR-p (通り)
| 確率は、 | q-1Cp-1・N-qCR-p NCR |
◆出題者のコメント。
完璧です!
ヨッシー さんには易しすぎたかも・・
【問題2−2】は【問題2】の後半をさらに一般化させたものです。
無理矢理パスカルの三角形で見てみると以下になります。
一般化すると 0C0 は q=1 や q=N の時に使用します。
【問題1】を例にしています。
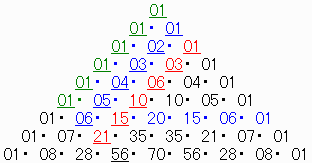
上の 56(=8C3) が求める確率の分母になります。
21(=8-1C3-1) から
左上に 21,06,01 、
右上に 21,15,10,06,
03,01 ですが、
それらとそれらに挟まれている上側のすべての数字を使用します。
この中でお互いにすぐ右上やすぐ左下にある数字同士を結んで1つのグループにします。
グループの数は3個(=R)で、各グループの要素の数は6個(=N−R+1)です。
そこで、左からと右からのそれぞれp番目(1≦p≦3(=R))に当たる2個のグループの各要素同士を掛けます。
ただし、左からのグループの各要素は上から、右からのグループの各要素は下から掛けます。
結果のグループの各要素こそが、3個(=R)でp番だった玉が8個(=N)で
p番,p+1番,・・,8−3+p(=N−R+p)番になる各々の確率の分子になります。
3個で1番の玉 (01,01,01,01,01,01)X(21,15,10,06,03,01)=(21,15,10,06,03,01) 3個で2番の玉 (01,02,03,04,05,06)X(06,05,04,03,02,01)=(06,10,12,12,10,06) 3個で3番の玉 (01,03,06,10,15,21)X(01,01,01,01,01,01)=(01,03,06,10,15,21)【余談】
【問題2】の結果を利用すると、シードも含めて抽選で決めたようなトーナメント戦では、途中まで勝ち残った者が大会で優勝する確率が容易に計算できます。
ただし、いつの状態でも勝ち残っている者同士の強さがまったく不明であることが条件です。
また、シードがあった場合は対戦者同士の勝率は必ずしも
| 1 2 | ずつにはなりません。 |
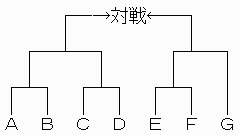
上の場合、
| 左の対戦者の勝率= | 7-1C4-1 7C4 |
| 右の対戦者の勝率= | 7-1C3-1 7C3 |
左と右の対戦者がそれぞれH人,M人の内で1番とし式を変形すると、 対戦する2人の勝率は以下になります。
| 左の対戦者の勝率= | H H+M |
| 右の対戦者の勝率= | M H+M |