『シムソン線』解答

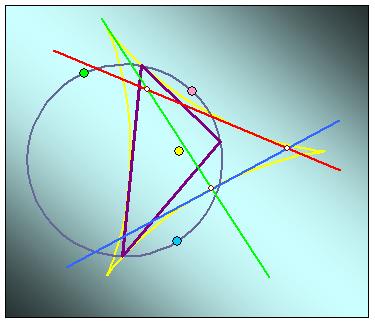
◆愛知県　Y.M.Ojisan さんからの解答。

ここでの特別な記法として　３要素ベクトル
(f(a,b,c),f(b,c,a),f(c,a,b))を[a,b,c▽f(a,b,c)] で表わし
要素の総和をΣ[a,b,c▽f(a,b,c)]で表わすこととする。

例えば　（Ａ、Ｂ、Ｃ）＝[α,β,γ▽(cosα,sinα)]である。

【問題１】

与式を書き直すと

（BC⊥、CA⊥、AB⊥）：[α,β,γ▽(cosγ−cosβ)x＋(sinγ−sinβ)y]＝[ｐ, ｑ, ｒ▽ｐ]

である。直交線の３式を左辺右辺合計すれば

　Σ[α,β,γ▽(cosγ−cosβ)x＋(sinγ−sinβ)y]
＝Σ[α,β,γ▽(cosα−cosα)x＋(sinα−sinα)y]
＝０ｘ＋０ｙ
＝０

　また、　Σ[ｐ, ｑ, ｒ▽ｐ]＝ｐ＋ｑ＋ｒ

よって、ｐ＋ｑ＋ｒ＝０　であることが必要である。

【問題２】

α＋β＋γ＝Ω　とする。

　[ｐ, ｑ, ｒ▽ｐ]
＝[α,β,γ▽sin(α＋γ)−sin(α＋β)]
＝[α,β,γ▽sin(Ω−β)−sin(Ω−γ)]
＝[α,β,γ▽sin(Ω)（cosβ−cosγ）−cos (Ω)（sinβ−sinγ）]

また

　（BC⊥、CA⊥、AB⊥）：[ｐ, ｑ, ｒ▽ｐ]＝[α,β,γ▽(cosγ−cosβ)x＋(sinγ−sinβ)y]

であるから

　[α,β,γ▽(cosγ−cosβ)(x＋sin(Ω))＋(sinγ−sinβ)(y− cos (Ω))]＝（０、０、０）

つまり　x=− sin(Ω) y= cos (Ω) であり、ｘ^２＋ｙ^２＝１

ただし、係数行列のＲＡＮＫが２以上の場合である。
つまりＡ≠Ｂ≠Ｃ≠Ａである場合。
以後も仮定する。

任意のtに対しては

　[ｐ, ｑ, ｒ▽ｐ]
＝[α,β,γ▽sin(α＋γ)−sin(α＋β)]*sin(t)＋[α,β,γ▽cos(α＋γ)−cos(α＋β)］*cos(t)
＝[α,β,γ▽sin(Ω−β)−sin(Ω−γ)]*sin(t)＋[α,β,γ▽cos(Ω−β)−cos(Ω−γ)]*cos(t)
＝[α,β,γ▽sin(Ω)（cosβ−cosγ）−cos (Ω)（sinβ−sinγ）]*sin(t)＋[α,β,γ▽cos(Ω)（cosβ−cosγ）＋sin (Ω) （sinβ−sinγ）]*cos(t)
＝[α,β,γ▽（cosβ−cosγ）(sin(t)*sin(Ω)＋cos(t)*cos(Ω))]＋　[α,β,γ▽（sinβ−sinγ）(−sin(t)*cos(Ω)＋cos(t)*sin(Ω))]

つまり、（ｘ、ｙ）＝（cos(θ)、ｓｉｎ(θ)）と置くということである。
　
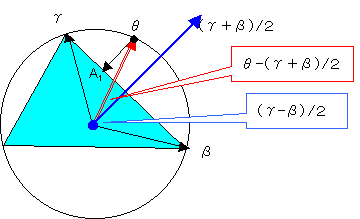
答えの方を変形すると、

Ａ１：(cos(

β＋γ 2

)*cos(

β−γ 2

)−sin(

β＋γ 2

)*sin(θ−

β＋γ 2

),sin(

β＋γ 2

)*cos(

β−γ 2

)＋cos(

β＋γ 2

)*sin(θ−

β＋γ 2

)

である。

図形を作図すれば、

ＢＣ⊥の方向：偏角

β＋γ 2

にcos(

β−γ 2

)、

ＢＣの方向にsin(θ−

β＋γ 2

)の点であるから、

ＰのＢＣへの垂線の足である。
B1,C1も輪換対称であり同様である。




【問題４】

ｌ(x , y ,θ) ：x*sinφ−y*cosφ　にＡ１点座標を代入し計算すれば

　2*l(A1,θ)= sin(φ−β)＋sin(φ−γ)−sin(φ−（β＋γ−θ）)＋sin(φ−θ)

である。

　２（−φ＋ （β＋γ−θ））＝−α−β−γ＋θ＋２β＋２γ−２θ=−α＋β＋γ−θ
　２（φ−α）＝α＋β＋γ−θ−２α＝−α＋β＋γ−θ

で両者は等しい。よって、

l(A1,θ)=（sin(φ−β)＋sin(φ−γ)＋sin(φ−α)＋sin(φ−θ)）/2である。

B1,C1の場合も輪換対称であり同様である。

【問題５】

この場合、方向に特異性は無いのでα、β、γ、θ_i全体を回転させて
α＋β＋γ＝０としても一般性を失わない。

なおその回転角は

α＋β＋γ ３

である。

またこの場合θ_i＝−２φ_iである。

さて、問題４で得られた直線の式を変形すると、

　x*sinφ_i−y*cosφ_i

＝	（cosα＋cosβ＋cosγ）sinφi−（sinα＋sinβ＋sinγ）cosφi＋sin（３φi） 2

である。

s₁*sinφ₁＋s₂*sinφ₂＋s₃sinφ₃＝０
s₁*cosφ₁＋s₂*cosφ₂＋s₃cosφ₃＝０

である全部がゼロではないs_iで重み付けをして左辺、右辺を足せば
s₁*sin（３φ₁）＋s_２*sin（３φ₂）＋s_３sin（３φ₃）＝０
でなければならない。

従って、全部がゼロではないs_iが存在するには



と置くとき｜D｜＝０でなければならない。

Φ＝φ₁＋φ₂＋φ₃とし、複素数を使って計算すると　
｜D｜=Σ[φ₁, φ₂, φ_３▽Im(exp((φ₁−φ₂)i)(exp(3φ₃i)− exp(3φ₃i))/2i]
　　　＝−Re｛ Σ[φ₁, φ₂, φ₃▽exp((φ₁−φ₂＋3φ₃)i)− exp((φ₁−φ₂−3φ₃)i)] ｝/2
　　　＝−Re｛ Σ[φ₁, φ₂, φ₃▽exp((Φ−2φ₂＋2φ₃)i)− exp((2φ₁−Φ−2φ₃)i)] ｝/2
　　　＝−Re｛ Σ[φ₁, φ₂, φ₃▽exp((Φ−2φ₂＋2φ₃)i)− exp((2φ₃−Φ−2φ₂)i)] ｝/2
　　　＝ Im｛ Σ[φ₁, φ₂, φ₃▽exp((2φ₃−2φ₂)i) *sin(Φ)] ｝
＝ Σ[φ₁, φ_２, φ₃▽sin(2φ₃−2φ₂)]*sin(Φ)
＝ 4*sin(φ₃−φ₂)*sin(φ₂−φ₁)*sin(φ₁−φ3)*sin(Φ)

Ａ≠Ｂ≠Ｃ≠Ａ であるから、
φ₁＋φ₂＋φ₃＝−ｎπのときのみ｜D｜＝0である。
θに戻せば　θ₁＋θ₂＋θ₃＝２ｎπ　のときであり、さらに最初の回転を戻せば
θ₁＋θ₂＋θ₃＝α＋β＋γ＋２ｎπ　である。


【問題６】

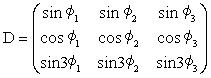
一般性を失わずα＋β＋γ＝０で考えます。
問題４より、シムソン線は下記です。

sinφi*（ｘ−

cosα＋cosβ＋cosγ 2

）−cosφi*（ｙ−

sinα＋sinβ＋sinγ 2

）＝

sin（３φi） 2

つまり　

（

cosα＋cosβ＋cosγ 2

，

sinα＋sinβ＋sinγ 2

）

を中心として３葉対称で回っている傾きtanφ_iの直線です。

　図を描けば　θ_１＝α＋π、θ_２＝β＋π、θ_３＝γ＋πのとき、シムソン線で囲まれた三角形が元の三角形に一致することは、直径の円周角が直角であることから明らかです。
即ち、θ_１−α＝θ_２−β＝θ_３−γ＝πのとき合同です。

よって、先に示した３葉対称性から、

θ１−α＝θ２−β＝θ３−γ＝

（２ｎ＋１）π ３

のときシムソン線で囲まれた三角形は元の三角形に合同です。



一方、合同であるためには、少なくとも相似でなければなりません。
θ_i＝−２φ_iであるので、θとシムソン線は１対１に対応しています。
従って裏表逆の合同も考えると　θ₁±α＝θ₂±β＝θ₃±γ＝Ｗ （複合同順） でなければなりません。
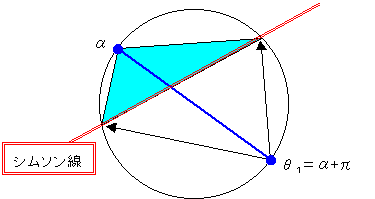
よって θ₁＋θ₂＋θ₃＝３W±（α＋β＋γ）＝３W＝（２ｎ＋１）πです。
すなわち

Ｗ＝

(２n＋１)π ３

【蛇足】

sin（φ＋ｄ）*Ｘ−cos（φ＋ｄ）*Ｙ＝

sin（３（φ＋ｄ）） 2

sin（φ−ｄ）*Ｘ−cos（φ−ｄ）*Ｙ＝

sin（３（φ−ｄ）） 2

の交点を計算すると

Ｘ＝

cos(4*φ) 2

＋cos(−2*φ)*cos(2d)

Ｙ＝

sin(4*φ) 2

＋sin(−2*φ)*cos(2d)

（ この問題の発端となった曲線が、内トロコイドであることが確定しました。）

つまり　φ＋ｄ＝φ_１　φ−ｄ＝φ₂　とすれば　

2*φ12＝（φ1＋φ2）＝−

α＋β 2

−W

2*ｄ12＝（φ1−φ2）＝

β―α 2

です。

複素数Ａ、Ｂ、Ｃを頂点とする三角形の面積が
　
の絶対値であることを使うと、シムソン線で囲まれた同じ向きの三角形の面積Ｇは下記である。

　４Ｇ＝｜Im｛ Σ[α，β，γ▽(exp((γ−２Ｗ)i)＋exp((W＋α)i)＋exp((W＋β)i))*(exp(−(α−２Ｗ)i)＋exp(−(W＋β)i)＋exp(−(W＋γ)i))] ｝｜

　＝｜Im｛Σ[α，β，γ▽(exp((γ−２Ｗ)i)−exp((W＋γ)i))*(exp(−α＋２Ｗ)i)−exp(−W−α)i] ｝｜
　＝｜Im｛Σ[α，β，γ▽(２*exp((γ−α)i)−exp((３W＋γ−α)i))−exp((−３W＋γ−α)i)] ｝｜
　＝２｜Σ[α，β，γ▽sin(γ−α)]｜*（１−ｃｏｓ（３Ｗ））

下図をクリックするとアニメーションがスタートします。
（５００ｋバイトでチョット重い）

全て三角関数数式処理でと思ったのですが、力及ばず幾何と複素数に流れました。
シムソン線はなかなかに優美な動きをするものです。しばし耽溺。

　『シムソン線』へ

　数学の部屋へもどる