『四面体』解答

◆山梨県　Footmark さんからの解答。

面倒な計算は一切省いた、直感的な証明です。

【問題１】

(a)，(b)は同値であると言える。

[証明]

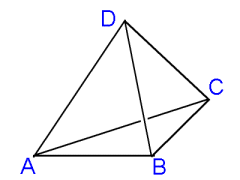
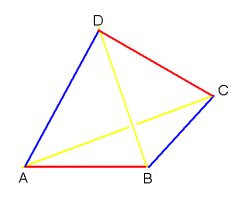
与えられた四面体を建築物と考え、４つの壁(面)を取り外し６つの梁(辺)だけにします。
また、４つの等しい角度をαとします。

上図で点Ｂと点Ｄの距離を拘束している梁(辺)ＢＤを取り外して、梁(辺)ＡＣを軸にして，三角形ＣＤＡが三角形ＡＢＣの反対側の同一平面上になるようにさせます。

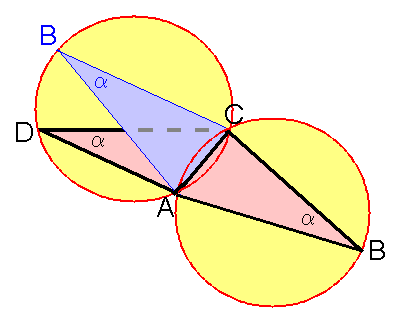
上図のように ∠ＤＡＢや∠ＢＣＤ は、梁(辺)ＡＣに対して点Ｂと点Ｄが反対側にあり４点が同一平面上にある時(開ききった状態)、最大になります。
また、梁(辺)ＡＣに対して点Ｂと点Ｄが同一側にあり４点が同一平面上にある時(畳みきった状態)、最小になります。
このことを利用します。

上図の四角形ＡＢＣＤにおいて、
題意より、∠ＡＢＣ＝∠ＣＤＡ＝α です。

この開ききった状態で ∠ＤＡＢ＝∠ＢＣＤ ならば、梁(辺)ＡＣを軸に点Ｂを動かし
∠ＤＡＢ＝α になるようにすれば、 対称性から必ず ∠ＢＣＤ＝α になる筈です。

そこで開ききった状態で ∠ＤＡＢ≠∠ＢＣＤ の場合を考えてみます。

上図のように梁(辺)ＡＣを軸に点Ｂを点Ｄと同じ側に折り畳んでみます。
畳みきった状態では ∠ＤＡＢ も ∠ＢＣＤ も左の円の弧ＢＤの張る円周角ですから
∠ＤＡＢ＝∠ＢＣＤ の筈です。

ところが畳みきった状態以外なら常に ∠ＤＡＢ≠∠ＢＣＤ で、２角の大小関係は開ききった状態の時と同じ筈です。

ですから開ききった状態で ∠ＤＡＢ≠∠ＢＣＤ なら、与えられた四面体ではありません。
与えられた四面体ならば開ききった四角形は向かいあった角が等しいので平行四辺形になります。

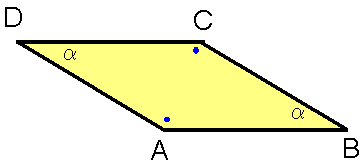
もし、∠ＡＢＣ＝∠ＣＤＡ＝α＞ π
２		 なら、

当然開ききった状態では
∠ＤＡＢ＝∠ＢＣＤ＜ π
２		 ですから、

常に ∠ＡＢＣ＝∠ＣＤＡ＝α＞∠ＤＡＢ＝∠ＢＣＤ で与えられた四面体にはなりません。

また、∠ＡＢＣ＝∠ＣＤＡ＝α＝ π
２		 なら、

当然開ききった状態では
∠ＤＡＢ＝∠ＢＣＤ＝ π
２

開ききった状態の時に限り、
∠ＤＡＢ＝∠ＡＢＣ＝∠ＢＣＤ＝∠ＣＤＡ＝αです。
しかし、これは四面体ではありません。

開ききった状態以外なら常に
∠ＡＢＣ＝∠ＣＤＡ＝α＞∠ＤＡＢ＝∠ＢＣＤ で、与えられた四面体にはなりません。

これらより、与えられた四面体なら
∠ＡＢＣ＝∠ＣＤＡ＝α＜ π
２		 ・・・（１）

（青色のＣである∠ＤＣＡと赤色のＣである∠ＤＡＣはいずれも π
２		 ）

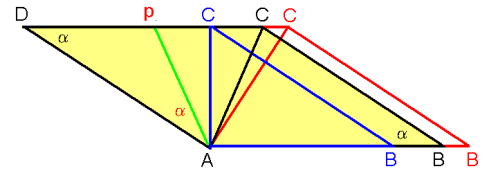
上図で点Ｂ,点Ｃが青色の時の平行四辺形を梁(辺)ＡＣを軸に点Ｂを点Ｄと同じ側に折り畳んでみます。
畳みきった時に限り、互いに錯角で
　 ∠ＤＡＢ＝∠ＣＤＡ、∠ＢＣＤ＝∠ＡＢＣ になります。

ですから、∠ＤＡＢ＝∠ＡＢＣ＝∠ＢＣＤ＝∠ＣＤＡ＝α です。
しかし、これは四面体ではありません。

畳みきった状態以外なら常に
∠ＡＢＣ＝∠ＣＤＡ＜∠ＤＡＢ＝∠ＢＣＤ で、
与えられた四面体にはなりません。

また上図で点Ｂ点Ｃの位置が青色より左側ならば点Ｂをどのように動かそうと、常に
∠ＡＢＣ＝∠ＣＤＡ＜∠ＤＡＢ＝∠ＢＣＤ で与えられた四面体にはなりません。

これらより、与えられた四面体なら
∠ＡＣＤ＝∠ＣＡＢ＜ π
２		 ・・・（２）

上図で点Ｂ,点Ｃが赤色の時の平行四辺形を梁(辺)ＡＣを軸にして点Ｂを点Ｄと同じ側に折り畳んでみます。
畳みきった時に限り、
∠ＤＡＢ＝∠ＣＤＡ、∠ＢＣＤ＝∠ＡＢＣ になります。

ですから、∠ＤＡＢ＝∠ＡＢＣ＝∠ＢＣＤ＝∠ＣＤＡ＝α です。

何故なら、梁(辺)ＡＢが直線Ａｐに重なったとすると
∠ＤＡＢ＝∠ＤＡｐ です。

また、∠ＤＡＣ＝∠ＢＣＡ＝ π
２		 ですから，
∠ＤＡｐ＋∠ｐＡＣ＝ π
２
∠ＡＢＣ＋∠ＣＡＢ＝ π
２

ところが，梁(辺)ＡＣを軸にして梁(辺)ＡＢが直線Ａｐに重なったのですから、
∠ｐＡＣ＝∠ＣＡＢ

それ故、∠ＤＡｐ＝∠ＡＢＣ
結局折り畳むと、∠ＤＡＢ＝∠ＡＢＣ
対称性から同様に ∠ＢＣＤ＝∠ＣＤＡですから、
∠ＤＡＢ＝∠ＡＢＣ＝∠ＢＣＤ＝∠ＣＤＡ＝α です。
しかし、これは四面体ではありません。

畳みきった状態以外なら常に
∠ＡＢＣ＝∠ＣＤＡ＜∠ＤＡＢ＝∠ＢＣＤ で、与えられた四面体にはなりません。

また上図で点Ｂ点Ｃの位置が赤色より右側ならば点Ｂをどのように動かそうと、
常に ∠ＡＢＣ＝∠ＣＤＡ＜∠ＤＡＢ＝∠ＢＣＤ で与えられた四面体にはなりません。

これらより、与えられた四面体なら
∠ＤＡＣ＝∠ＢＣＡ＜ π
２		 ・・・（３）

点Ｂ点Ｃの位置が青色より右で赤色より左なら、畳みきった状態では図からも明らかのように
∠ＤＡＢ＝∠ＢＣＤ＜α です。

また開ききった状態では（１）より、
∠ＡＢＣ＝∠ＣＤＡ＝α＜ π
２		 ですから
∠ＤＡＢ＝∠ＢＣＤ＞ π
２

ですから、∠ＤＡＢ＝∠ＢＣＤ＞α です。

それ故、梁(辺)ＡＣを軸に点Ｂを動かして畳みきった状態から開ききった状態にする過程で、
必ず ∠ＤＡＢ＝∠ＢＣＤ＝α　となる点Ｂの位置がある筈です。

そのとき４つの三角形はいずれも２辺と挟む角(α)が等しいため合同です。
しかも、（１）,（２）,（３）より三角形の３つの角はいずれも鋭角でなければなりません。

逆に上図のように４つの三角形が合同な鋭角三角形なら、
∠ＤＡＢ＝∠ＡＢＣ＝∠ＢＣＤ＝∠ＣＤＡ です。

何故なら、図で同色の辺が長さが等しいものとすると、
４つの三角形はいずれも赤色と青色と黄色の辺で構成されていますが、
∠ＤＡＢ、∠ＡＢＣ、∠ＢＣＤ、∠ＣＤＡのいずれの角も青色の辺と赤色の辺の挟む角ですから等しい筈です。

証明は終わりです。

【問題２】

空間の異なる４点を考えると、４点とも同一平面上にある時とそうでない時があります。

[４点が同一平面上にある時]

次の３つの場合があります。

（１）４点が同一直線上にある時

点Ａ、点Ｂ、点Ｃ、点Ｄの並び方で

∠ＤＡＢ＋∠ＡＢＣ＋∠ＢＣＤ＋∠ＣＤＡ＝（０°Ｘ４）＝０°
∠ＤＡＢ＋∠ＡＢＣ＋∠ＢＣＤ＋∠ＣＤＡ
＝（０°ｘ２）＋（１８０°ｘ２）
＝３６０°

の２通りしかありません。

（２）３点が同一直線上にある時

線分ＡＢ，線分ＢＣ，線分ＣＤ，線分ＤＡを書き込めば必ず１つの三角形が形成されます。
４点の内で三角形の頂点にならない点は、三角形の辺上にあるか、辺の延長上にあります。

辺上にある時
∠ＤＡＢ＋∠ＡＢＣ＋∠ＢＣＤ＋∠ＣＤＡ
＝三角形の３つの内角の和＋１８０°
＝３６０°

辺の延長上にある時
∠ＤＡＢ＋∠ＡＢＣ＋∠ＢＣＤ＋∠ＣＤＡ
＝（三角形の２つの内角の和）Ｘ２　
＜３６０°

何故なら（三角形の３つの内角の和）Ｘ２＝３６０°

（３）どの３点も同一直線上にない時

線分ＡＢ，線分ＢＣ，線分ＣＤ，線分ＤＡを書き込んでみます。
基本的には下の図の３つのケースしかありません。

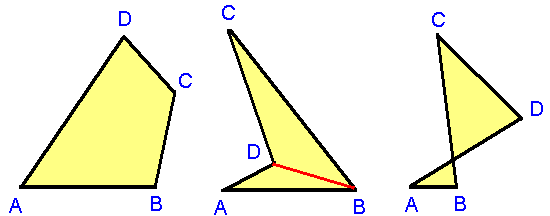
左の図の場合凸四角形ですから、
∠ＤＡＢ＋∠ＡＢＣ＋∠ＢＣＤ＋∠ＣＤＡ＝３６０°

中央の図の場合∠ＣＤＡが大きい方をとっても、２つの三角形の６つの内角の和ですから、
∠ＤＡＢ＋∠ＡＢＣ＋∠ＢＣＤ＋∠ＣＤＡ＝３６０°

右の図の場合２つの三角形の４つの内角の和ですから、
∠ＤＡＢ＋∠ＡＢＣ＋∠ＢＣＤ＋∠ＣＤＡ＜３６０°

[４点が同一平面上にない時]

空間の異なる３点は１つの平面を決定しますから、３点は必ず同一平面上にあります。
ですから点Ａ,点Ｂ,点Ｃは同一平面上にあります。

点Ｄ点Ｂ間以外の他の２点間の距離を一定に保ったままで点Ｄを点Ｂからできるだけ遠ざけると、４点は同一平面上に存在し、線分ＡＢ，線分ＢＣ，線分ＣＤ，線分ＤＡを書き込めば凸四角形ＡＢＣＤが形成されます。

この時、∠ＡＢＣと∠ＣＤＡは不変ですが
∠ＤＡＢと∠ＢＣＤは最大になります。

最大になった時でも、凸四角形ＡＢＣＤですから、

∠ＤＡＢ＋∠ＡＢＣ＋∠ＢＣＤ＋∠ＣＤＡ＝３６０°

ですから、点Ｄ点Ｂ間以外の他の２点間の距離を一定に保ったままで点Ｄが他の３点と同一平面上でないように、点Ｄの位置を変えると、

∠ＤＡＢ＋∠ＡＢＣ＋∠ＢＣＤ＋∠ＣＤＡ＜３６０°

ですから、４点が同一平面上にない時は

∠ＤＡＢ＋∠ＡＢＣ＋∠ＢＣＤ＋∠ＣＤＡ＜３６０°

以上のことから、空間の異なる４点がどのようにあろうと常に
∠ＤＡＢ＋∠ＡＢＣ＋∠ＢＣＤ＋∠ＣＤＡ≦３６０°

証明は終わりです。

◆大阪府　macsyma2e さんからの解答。

【三面角(必要)条件】

3つの単位ベクトルのなす角度を x,y,z とすると、常に次が成り立ちます．

x + y ≧ z

証明　3つの単位ベクトルを

u(i) = ( u(i,1), u(i,2), u(i,3) ) (i=1,2,3)

とおくと、それらの張る平行六面体の体積の2乗は、

　det( (u(i,j))i,j ) × det( (u(j,i))i,j )
= det( ( 3
Σ
k=1		 u(i,k)×u(j,k) )i,j )
この行列式のi,j成分は i=j では 1、その他はなす角度の余弦なので、

= 1 + 2×cos(x)×cos(y)×cos(z) - cos(x)2 - cos(y)2 - cos(z)2
= ( sin(x)×sin(y) )2 - ( cos(x)×cos(y) - cos(z) )2
= 4×sin( x+y-z
2		 )×sin( x-y+z
2		 )×sin( -x+y+z
2		 )×sin( x+y+z
2		 ) ・・・・（★）
となり、この値は非負実数です．

さて、非自明な場合、つまり、0°≦ x,y < z ≦ 180°かつ x+y < 180°ならば

0°< -y+z ≦ x-y+z ≦ x+z < 360°
0°< -x+z ≦ -x+y+z ≦ y+z < 360°
0°< x+y+z < 360°

が成り立つので、
sin( x-y+z
2		 )×sin( -x+y+z
2		 )×sin( x+y+z
2		 ) > 0
よって、
sin( x+y-z
2		 ) ≧ 0
となり、-180°≦ x+y-z < 180°と併せて結果を得ます．

【問題１】

■ 四面体が「退化してもよい」という設定なら、同値ではありません．

退化しない任意の正方形 ABCD では、(a) は満たしますが、(b) の鋭角条件を満たしません．

■ 四面体が「退化しない」という設定なら、以下に見るように同値です．

(b) ならば (a) は、合同な三角形の対応する角度ゆえ、成立します．

逆に (a) のとき、その角度を t、線分 AC, DB, AB, BC, AD, DC の長さを各々 x,y,a,b,c,d として、x=y かつ a=d かつ b=c の成立を示します． 以下、四面体が退化しないので

0°< t < 180°
x,y,a,b,c,d > 0

です．まず、余弦定理により

x2 = a2 + b2 - 2×a×b×cos(t) ・・・・（１）
x2 = c2 + d2 - 2×c×d×cos(t) ・・・・（２）
y2 = b2 + d2 - 2×b×d×cos(t) ・・・・（３）
y2 = c2 + a2 - 2×c×a×cos(t) ・・・・（４）

ですが、（１）と（２）、（３）と（４）の右辺から

a2 + b2 - c2 - d2 = 2×( a×b - c×d )×cos(t) ・・・・（５）
d2 + b2 - c2 - a2 = 2×( d×b - c×a )×cos(t) ・・・・（６）

更に cos(t) の係数を揃えて、等置すると

( a2 + b2 - c2 - d2 )×( d×b - c×a )
= ( d2 + b2 - c2 - a2 )×( a×b - c×d )

整理して

( a-d )×( b-c )×( a-b-c+d )×( a+b+c+d ) = 0

を得ます．

a=d のとき、（１）（３）から x=y となり、
結果（１）（４）から b=c も判ります．

b=c のときも同様です．

a-b-c+d = 0 のときも、
a-b = c-d および b-d = a-c として辺々2乗すれば

a2 + b2 - c2 - d2 = 2×( a×b - c×d )
d2 + b2 - c2 - a2 = 2×( d×b - c×a )

であり、（５）（６）は

( a×b - c×d )×( cos(t) - 1 ) = 0
( d×b - c×a )×( cos(t) - 1 ) = 0

となって、0°< t から

a×b = c×d
d×b = c×a

つまり、a=d かつ b=c に至り、
（１）（４）から x=y です．

ここまでで、四面体が等面であることが判りました．

そこで、改めて任意の面の3内角の大きさを s,t,u ( s≦t≦u ) とおくと、四面体の任意の頂点で【三面角条件】を適用すれば、直ちに

u ≦ s+t = 180°- u　つまり　u ≦ 90°

ですが、u = s+t ⇒（★）により四面体の体積 = 0 なので、
u < 90°です．

【問題２】

角度が 0°となるものも含めて、【三面角条件】から

　360°
= 180°+ 180°
= ( ∠DAC + ∠ACD + ∠CDA ) + ( ∠CAB + ∠BCA + ∠ABC )
= ( ∠DAC + ∠CAB ) + ∠ABC + ( ∠BCA + ∠ACD ) + ∠CDA
≧ ∠DAB + ∠ABC + ∠BCD + ∠CDA．

【ひとこと】

「 補助線 」や「 移動 」は苦手です．

　『四面体』へ

　数学の部屋へもどる