◆東京都の中学校１年生 安里歩安彼 さんからの解答。
僕がいままで出会った数学の証明のなかで、最も美しいと思ったのは、次の証明です。
定理：
素数は自然数の中で無限にある。
証明：
もし、素数が有限個あるとして、それを
ｐ1、ｐ2、…ｐnとする。
このとき、X＝ｐ1・ｐ2・…・ｐn＋１について、
(1) Xが素数である
最大の素数はｐnであるので、ｐn＜Xとなり、矛盾。
(2) Xが合成数である
もしそうだと、ある素数ｐi ｜ Xである。
しかし、任意の素数ｐjにたいし、
X≡１（modｐj）となるので、矛盾。
どちらにしても矛盾なので、命題は示された。
実際に矛盾の起こる数として、ｐ1・ｐ2・…・ｐn＋１を構成したEuclidの着想の奇抜さに感嘆してしまいますし、ほんとうに簡潔で、見るだけで楽しくなる証明だと思います。
【コメント】
もう本は忘れてしまいましたが、昔、次のような趣旨のことをメモしました。
この定理の別証明としてEulerの式を使う方法があります。
証明：
素数が有限個２，３，・・・，ｐnであるとする。
| Ｓ＝１／ | n Π i＝1 | (1- | 1 ―― pi | ) | ＝ | n Π i＝1 | (1+ | 1 ―― pi | + | 1 ―― pi2 | +･･･) |
右辺を展開すると
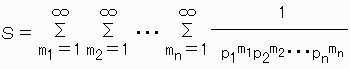
右辺の
は任意の自然数を素因数分解した形に一致するから、素因数分解の一意性より
| Ｓ＝ | ∞ Σ n＝1 | 1 ―― n |
ところがこの無限級数は発散することがよく知られており、Ｓの定義に矛盾する。
したがって素数は有限個ではない。 証明終
筆者はこの証明の方が自然なのではないかと主張していました。
それはEuclidの証明のようにたった一つの例を示すだけではなく、有限個の素数をいくら掛け合わせても無限にある全ての自然数を表すには不足であることを直接、量的に示しているからだという意味です。
例えで言うと、入試に落ちた人に向かって、「あなたの答案はここが間違っているよ。」と一箇所だけ誤りを指摘するのと、「あなたの学力ではとうてい無理ですよ。」と指摘するのの違いだと言います。
同じ落第しても、後者の方があきらめがつくのでは？？？。
判断は皆さんにお任せします。