◆神奈川県 いわし さんからの解答。
[命題]
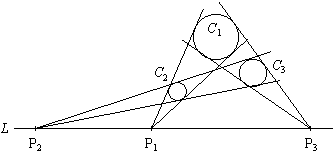
平面上に半径の異なる3つの円C1,C2,C3 があり、
C1とC2,C2とC3,C3とC1の共通外接線の交点をそれぞれ
P1,P2,P3とすると、P1,P2,P3は同一直線L上にあります。
[証明]
C1,C2,C3を大円に持つ球をそれぞれ
S1,S2,S3とします。
S1とS2,S2とS3,S3とS1に外接する、頂点が2球の間にない円錐をそれぞれ
K1,K2,K3とすると、それらの頂点はP1,P2,P3に一致します。
S1,S2,S3に接し、S1,S2,S3を一方の側に持つ平面を
π1,π2とすると、K1,K2,K3もπ1,π2に接しますから、
P1,P2,P3はπ1,π2の交線L上にあります。 (終)

小学生か中学生のころ、多分本で読んだと思うのですが、鮮やかさに感動したのを覚えています。
今思うと、直感的過ぎるような気もしますが、平面の問題に立体を持ち出すという発想は卓越していると思います。