数学の美しさ

『数学の美しさ』解答

◆埼玉県の中学校３年生　田沼　和泰 さんからの解答。

高校受験の勉強の際によく図書館に行きました。
その時に見た数学辞典にあったヒポクラテスの月形に感動しました。

  1. 半円を描く。

  2. その半円の直径を長辺とし、頂点を半円の孤の上に持つ直角三角形ＡＢＣを描く。
    　　（孤の上の点をＡ、他の二点をＢ，Ｃとする）

  3. 辺ＡＢ、辺ＡＣをそれぞれ直径とする半円を外向きに描く。
    このとき、半円ＢＣからはみ出た部分の面積は、直角三角形ＡＢＣの面積と等しい。

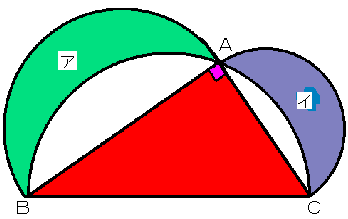
半円ＢＣからはみ出た部分の面積のうち、半円ＡＢの一部のものをア、半円ＡＣの一部のものをイとすると
ア＋イ＝△ＡＢＣ

◆自分なりの証明

  1. 三平方の定理より、
    ＡＢ2＋ＡＣ2＝ＢＣ2

  2. 両辺を８で割って、πを掛けると

    ＡＢ2π
    ８    		 ＋ＡＣ2π
    ８    		 ＝ＢＣ2π
    ８

    となり、これは
    半円ＡＢ ＋半円ＡＣ ＝半円ＢＣを表す式である。

  3. 半円ＡＢ・半円ＡＣと半円ＢＣの共通部分の面積を引くと、ヒポクラテスの月形が成り立つ。
下手な証明で申し訳ない。
しかし自分の中ではとてもわかりやすい証明方法です。
図も簡素な上、これだけ美しい関係があるなんてなんて素晴らしいのだろうと、受験勉強も投げ出して感動したものでした。

　数学の美しさへもどる

　数学の部屋へもどる