とすぐわかりますが、一般的な答えを求めてみます。◆石川県 平田 和弘 さんからの解答
【問題１】
特殊な例(正三角形)で考えると答えはとすぐわかりますが、一般的な答えを求めてみます。
△ABCの面積＝△ABDの面積＋△ACDの面積 より
| 1 ― 2 | ･AB･AC･sin60° |
| = | 1 ― 2 | ･AB･AD･sin30°+ | 1 ― 2 | ･AC･AD･sin30° |
よって
・AB・AC＝AD(AB＋AC)
従って、
| ＝ | AD(AB＋AC) ―――――――― AB・AC |
| ＝ | AD ――― AC | ＋ | AD ――― AB |
となり、求める答えはとなります。
◆埼玉県 斉藤 誠 さんからの解答。
【問題２】
（１）
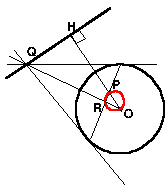
円Ｏの中心からＰを通る弦に下ろした垂線の足をＲとする。
弦の両端と円の中心Ｏを結ぶと２等辺三角形になるので、この点Ｒは弦の中点である。
∠ＯＲＰ＝∠Ｒ（直角）
なので、点ＲはＯＰを直径とする円上（点Ｏを除く）を動く。
（２）
ＯＰの延長線上にＯＰ⊥ＱＨとなる点Ｈをとると
△ＯＲＰ∽△ＯＨＰ
となり、点Ｑの位置に関係なくこの相似条件は満足する。
よって、点Ｑの軌跡は直線ＱＨにある。
（ただし、弦がＯＰに一致するときを除く）
【問題３】
直線Ｌに定点Ｐから下ろした垂線の足をＨとする。
直線ＰＱの１／Ｔの位置に点Ｒをとる。
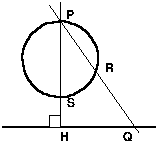
また、直線ＰＨの１／Ｔの位置に点Ｓをとると
ＰＲ×ＰＱ＝ＰＨ×ＰＳ＝Ｔ
である。
よって、
ＰＲ／ＰＨ＝ＰＳ／ＰＨ
すなわち
ＰＲ：ＰＨ＝ＰＳ：ＰＱ
となり、△ＰＲＳ∽△ＰＨＱとなるので
∠ＰＲＳ＝∠Ｒ（直角）
故に点Ｒの軌跡はＰＳを直径とする円上（点Ｐを除く）を動く