『頂点と接点を結ぶと？』 解答

◆愛知県　Y.M.Ojisan さんからの解答。

【中心解答】

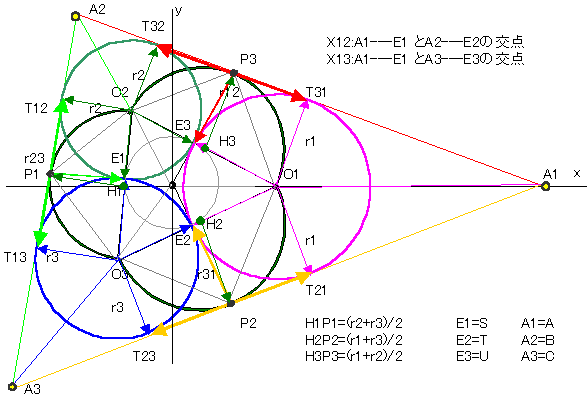
下図のように記号を定義する。
点A,B,C,S,T,U は便宜上添え字付記号に変更した。

E₁，E₂，E₃は△O₁O₂O₃の内接円の接点であるので、内接円の中心Oを原点とし、
∠E₃OE₂の２等分線(O1の方向)をｘ軸とする直交座標 {ｘ , ｙ} で考える。

また、代表長を内接円の半径とし、１単位とする。
すなわち、

｜OE_i|=１　 i=1,2,3　　　―――(１)

である。

以降添え字iは　1,2,3を　
^iは ^1==23,^2==31,^3==12　を一般的に表しているとする。
また添え字　i+kは　i+k mod 3　であるとする。

さらに
OE₃＝{x,y}
OE₂＝{x,-y}
OE₁＝{-αx,βy}　と置く。

ただし、α＞１　｜β｜＜１　である。

(１)より

ｘ²+ｙ²=1
(αｘ)²+(βｙ)²=1　　―――(２)

でなければならず、

ｘ2＝	１−β2 α2−β2

ｙ2＝

α2−１ α2−β2

―――(３)

以降　X座標は　ｘ(≧０)　、Y座標はｙ(≧０)を単位とし、下記であらわす。

　[a,b] = (aｘ,bｙ)

なお、ベクトル　[a,b]と [c,d]　の内積は　行列計算では
[a,b]・Ｍ・[c,d] ^t　で計算される。
ここで　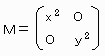　―――(４)

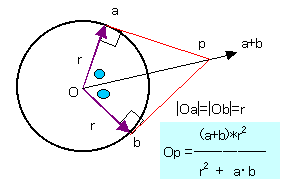
上図の関係　―――(５)を用いることにより、

Oi =

OEi+1+ OEi+2 1+[ OEi+1]Ｍ[OEi+2] t

―――(６)

である。これを計算すると、

O1=

[

α2−β2 １−β2

,0 ]

O2=

[

β−α １＋β

,

α−β α−１

] ―――――(７)

O3=

[

−(β＋α) １−β

,

−(α＋β) α−１

]

また、

｜E3O1|　=　r1　=√

(

α2−1 １−β2

)

｜E1O2|　=　r2　=√

{(

α＋1 α−1

)

×

(

１−β １＋β

)}

―――――(８)

｜E2O3|　=　r3　=√

{(

α＋1 α−1

)

×

(

１＋β １−β

)}

つぎに　

円O_iに外接する△A₁A₂A₃と円O_iの接点を図のように、
Ｔ₃₁、Ｔ₃₂、Ｔ₁₂、Ｔ₁₃、Ｔ₂₃、Ｔ₂₁とし、
O_iとO_i＋1の中点を Ｈ_i＋2、
Ｔ_i,i＋1とＴ_i,i＋2の中点をＰ_iとする。

このとき

｜ＨiＰi｜=

ri＋2 ＋ri＋1 ２

で

O_iＴ_i,Jと　Ｈ_JＰ_Jは平行である。――(９)

また、Ｐ_iはＯE_iの延長上にあることが容易にわかり、相似関係から計算すると

｜Ｐ_iE_i｜＝　r _^i＝√{ r_i＋2 ×r_i＋1}　である。
計算すると、

r23　=√

(

α＋1 α−1

)

r31　=√

(

α＋1 １−β

)

―――――(１０)

r12　=√

(

α＋1 １＋β

)

よって、

ＯＰ_i＝(１＋r _^i)ＯE_i

Ｈi＝

Oi＋1＋Oi＋2 ２

―――――(１１)

Ｐ_i＝　(１＋r _^i)E_i　　―――――(１２)

(５)および(９)の関係を適用すると

Ａi＝　Oi＋２ri×

(ri＋ri＋2)×Ｈi＋1Ｐi＋1＋(ri＋ri＋1)×Ｈi＋2Ｐi＋2 (ri＋ri＋2)×(ri＋ri＋1)＋４[Ｈi＋1Ｐi＋1]Ｍ[Ｈi＋2Ｐi＋2]t

―――(１３)

最後に　Ｅ_iとＡ_iを通る直線とＥ_ＪとＡ_Ｊを通る直線の交点をΩ_i,Jとするとき、

すなわち　下記連立線形方程式を解く必要がある。
なお、×：外積のＺ成分計算とする。

(Ａ_i− Ｅ_i)×　Ω_i,J＝(Ａ_i−Ｅ_i )× Ｅ_i

(Ａ_Ｊ−Ｅ_Ｊ)×　Ω_i,J＝(Ａ_Ｊ−Ｅ_Ｊ)× Ｅ_Ｊ　――(１４)

そこでまず、厄介な√を

α＝

θ４＋１ ２θ2

１＞θ＞０　　　　　―――(１５)

β＝

η４−６η２＋１ η４＋２η２＋１

１＞η＞０

で置き換えてはずす。このとき、

√｛2(α＋１)｝＝

θ2＋１ θ

√｛2(α−１)｝＝

θ2−１ θ

√｛2(１＋β)｝＝

2(η2−１) η2＋１

√｛2(１−β)｝＝

4η η2＋１

となり、θ　η　の有理多項式である。
またも以下のように相殺される。

r1　=	(θ４−１)(η2＋１) 2 ８θ２η(η2−１)

r2　=	２(θ2＋１)η (θ2−１)(η2−１)

r3　=	(θ2＋１)(η2−１) ２(θ2−１)η

r23　=

θ2＋１ θ2−１

r31　=

(θ2＋１)(η2＋１) 4θη

r12　=

(θ2＋１)(η2＋１) 2θ(η2−１)

ｒを求める式以外の計算は４則演算のみである。
よって、Ω_i,Jはθとηの整数係数の有理多項式である。

　(１２)式までは比較的容易にθとηによる関数式を求めることができ、多項式の次数がわかる。
また、(１３)および(１４)は四則演算のみであり、約分できない最悪の場合を考えることにより、多項式の最大次数がわかる。

　さらに、Ω_1,2―Ω_1,3を通分したあとの分子の整数係数多項式のθとηの最大次数を計算すると各々約４００以下であることが分かる。
詳細表１

　よって数値計算により、
値の異なる　θ方向３７８×η方向３８３以上の格子点上において、
ＤΩ＝Ω_1,2―Ω_1,3が０であれば、成立が証明される。

実際、１０００桁／１０００桁　の有理数計算ができるプログラムを作成し、

θ、η ＝

1 2

,

1 3

,

2 3

,

1 4

,

3 4

,

1 5

,

2 5

,

3 5

,

4 5

,

1 6

,………,

35 36

なる、一辺３９５個 の分母３６以下の有理数格子点約１６万点で
ＤΩ　を計算した。

η＝1/2　θ＝3/5　のような分母が０になる組や、桁あふれによる確認不良点があるかもしれないので余計に計算した。
その結果　各ηないしθにつき３９０個(＞３８２)以上の有効点で　ＤΩ＝０　であることを確認した。
なお実際には５０桁ほどで十分であり、桁あふれはなかった。

例として　２ケースの計算結果を下記に示す。
Ω＝Ω_1,2＝Ω_1,3

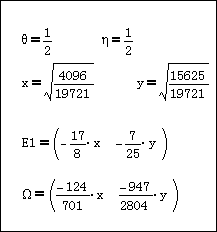
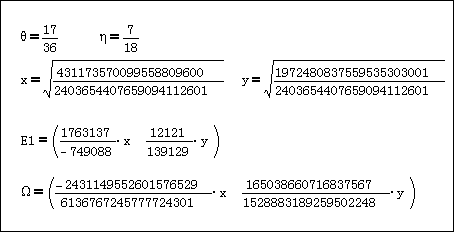
【感想】

　互いに内接したり外接したりする、円や３角形４角形が多数あって、とても綺麗な問題であると思いました。
従って、もっとエレガントに解きたかったのですが、簡単にはわからなかったことと、計算機で解く方法がおもしろそうだったのでこのような解となりました。

　そのため、この交点の本質が良く見えません。
三角形の５心の線形結合ではなさそうです。
三角形の第６心といってもいいかもしれませんね。

表１	[x,y]のｘ値 または　スカラー値					[x,y]のｙ値
	分子次数		分母次数			分子次数		分母次数
項目	θ最大	η最大	θ最大	η最大		θ最大	η最大	θ最大	η最大
Ｅ１	4	0	2	0		0	4	0	4
Ｅ２	0	0	0	0		0	0	0	0
Ｅ３	0	0	0	0		0	0	0	0
[1,1]Ｍ	4	6	8	8		8	8	8	8
Ｏ１	8	8	4	6		0	0	0	0
Ｏ２	4	4	2	4		4	4	4	4
Ｏ３	4	4	2	2		4	4	4	4
ｒ１	6	6	5	6
ｒ２	2	1	2	2
ｒ３	2	2	2	1
P1H1MP2H2	10	10	8	8
P1H1MP3H3	10	10	8	8
P2H2MP3H3	16	12	12	8
Ａ１	59	56	56	52		51	52	50	52
Ａ２	40	42	36	42		40	39	38	39
Ａ３	40	40	36	38		40	38	38	37
Ω１２	187	193	187	193		189	193	187	193
Ω１３	187	188	187	188		189	189	187	188
ＤΩ	374	381	374	381		376	382	374	381

◆宮城県　アンパンマン さんからの解答。

チェバの定理より次の定理が成り立つ。

定理：

三角形ABCと、辺BC上の点X、辺CA上の点Y、辺AB上の点Zが与えられたとする。
このとき、AX、BY、CZが一点で交わることと、次の条件は同値である。

sin(∠BAX) sin(∠XAC)

*

sin(∠CBY) sin(∠YBA)

*

sin(∠ACZ) sin(∠ZCB)

=1

(証明を省略)

Y.M Ojisan さんからの解答図より O_iの周りの角度を図のようにつける。

∀ i,j ∈{1,2,3,4}, i≠j、
α_ij=α_i+α_j,
β_ij=β_i+β_j,
γ_ij=γ_i+γ_jと定義する。

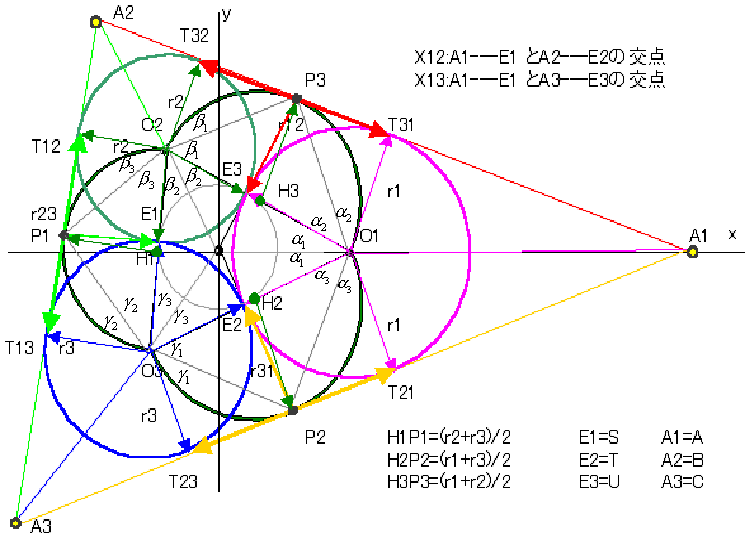
△A₃ T₁₂ E₃ を考えると
y_i=|A_i E_i|, i=1,2,3.

sin(∠T₁₂ A₃ E₃)

=	|T12 E3|*sin(∠ A3 T12 E3) |A3 E3|

=	|T12 E3|sin(β23) y3

=	2r2 sin2(β23) y3

同様に、△A₁ T₃₂ E₁ を考えると

sin(∠T32 A1 E1)=

2r2 sin2(β12) y1

つまり

sin(∠T12 A3 E3) sin(∠T32 A1 E1)

=

y1 y3

{

sin(β23) sin(β12)

}2

sin(β23) =

|OP1|cos(β2) |O2 P1|

同様に

sin(β12)=

|OP3|cos(β2) |O2 P3|

つまり、

sin(∠T12 A3 E3) sin(∠T32 A1 E1)

=

y1 y3

{

sin(β23) sin(β12)

}2

=

y1 y3

(

|OP1| |OP3|

)2

r22+r232 r22+r122

=

y1 y3

(

|OP1| |OP3|

)2

r2+r3 r2+r1

同様に

sin(∠T23 A1 E1) sin(∠T13 A2 E2)

=

y2 y1

(

|OP2| |OP1|

)2

r3+r1 r3+r2

sin(∠T31 A2 E2) sin(∠T21 A3 E3)

=

y3 y2

(

|OP3| |OP2|

)2

r1+r2 r1+r3

sin(∠T12 A3 E3) sin(∠T32 A1 E1)

*

sin(∠T23 A1 E1) sin(∠T13 A2 E2)

*

sin(∠T31 A2 E2) sin(∠T21 A3 E3)

＝１

であることより
A₁E₁, A₂E₂, A₃E₃は一点で交わる。

◆神奈川県　諏訪冬葉 さんからの解答。

O₁,O2,O3 の半径を p,q,r
この三角形の面積を V
この三角形の周囲の長さの半分を s
三頂点の位置ベクトルを A,B,C とおく

点 X=

lA l+m+n

+

mB l+m+n

+

nC l+m+n

をX{l：m：n} と略記する。

任意の点について
X{△BCX：△CAX：△ABX} が成り立つ。

O1{V-

p(b+c) 2

：

pb 2

：

pc 2

}

O2{

qa 2

：V-

q(a+c) 2

：

qc 2

}

O3{

ra 2

：

rb 2

：V-

r(a+b) 2

}

S=

rO2+qO3 q+r

などから

S{qra：r(V-q(s-b))：q(V-r(s-c))}
T{r(V-p(s-a))：prb：p(V-r(s-c))}
U{q(V-p(s-a))：p(V-q(s-b))：pqc}

OS が BC と交わる点を S' とすると

S'{0：r(V-q(s-b))：q(V-r(s-c))}
T'{r(V-p(s-a))：0：p(V-r(s-c))}
U'{q(V-p(s-a))：p(V-q(s-b))：0}

チェバの定理を使用すれば、分子も分母も
pqr(V-p(s-a))(V-q(s-b))(V-r(s-c)) となり成り立つ。

よって問題の三線は一点で交わる。

【コメント】

この交点ですが、「第１安島-Malfatti点」というようです。
参考リンク

http://cedar.evansville.edu/~ck6/tcenters/recent/ajmalf.html

◆宮城県　甘泉法師 さんからの解答。

解けていませんが道筋だけ示します。

∠A＝2α、∠B＝2β、∠C＝2γとする。

円Oi(i=1,2,3)の半径をriとして

辺ABの長さc=　r1cotα＋2√(r1r2)＋r2cotβ
辺BCの長さa=　r2cotβ＋2√(r2r3)＋r3cotγ
辺CAの長さb=　r3cotγ＋2√(r3r1)＋r1cotα

点B,Cはx軸上に点Aはy軸上正にあるようにｘｙ座標を導入する。

点A(0，c*sin2β)=(0，b*sin2γ)=(0，h)
点B(-c*cos2β，0)
点C(b*cos2γ，0) とすると

点O1(r1*cosecα*cos(2γ＋α)，c*sin2β-r1*cosecα*sin(2γ＋α))
点O2(-c*cos2β+r2cotβ，r2)
点O3(b*cos2γ-r3cotγ，r3)

点Sは線分O2O3をr2:r3に内分する点なので

点S

1 r2+r3

*(r3*(-c*cos2β+r2cotβ)+r2*(b*cos2γ-r3cotγ)，r3*r2+r2*r3)

点Tは線分O3O1をr3:r1に内分する点なので

点T

1 r3+r1

*(r1*(b*cos2γ-r3cotγ)+r3*r1*cosecα*cos(2γ＋α)，r1*r3+r3*{c*sin2β-r1*cosecα*sin(2γ＋α)})

点Uは線分O1O2をr1:r2に内分する点なので

点U

1 r1+r2

*(r2*r1*cosecα*cos(2γ＋α)+　r1*{-c*cos2β+r2cotβ}，r2*{c*sin2β-r1*cosecα*sin(2γ＋α)}　+　r1*r2)

直線ASの方程式

ｙ-c*sin2β x-0

=	2*r3*r2/(r2+r3)-c*sin2β r3*(-c*cos2β+r2cotβ)+r2*(b*cos2γ-r3cotγ)}/(r2+r3)-0

=	2*r3*r2-(r2+r3)*c*sin2β r3*(-c*cos2β+r2cotβ)+r2*(b*cos2γ-r3cotγ)

=ｋ

直線BTの方程式

ｙ-0 x+c*cos2β

=	[r1*r3+r3*{c*sin2β-r1*cosecα*sin(2γ＋α)}]/(r3+r1)-0 ｛r1*(b*cos2γ-r3cotγ)+r3*r1*cosecα*cos(2γ＋α)｝/(r3+r1)+c*cos2β

=	r1*r3+r3*{c*sin2β-r1*cosecα*sin(2γ＋α)} r1*(b*cos2γ-r3cotγ)+r3*r1*cosecα*cos(2γ＋α)+(r3+r1)*c*cos2β

=r3*	h-r1*cosecα*sin(2γ＋α)+r1 r1*(h*cot2γ-r3cotγ)+r3*r1*cosecα*cos(2γ＋α)+(r3+r1)*h*cot2β

=ｌ

直線CUの方程式

ｙ-0 x-b*cos2γ

=	[r2*{c*sin2β-r1*cosecα*sin(2γ＋α)}+r1*r2]/(r1+r2)-0 [r2*r1*cosecα*cos(2γ＋α)+　r1*{-c*cos2β+r2cotβ}]/(r1+r2)-b*cos2γ

=	[r2*{c*sin2β-r1*cosecα*sin(2γ＋α)}+r1*r2] r2*r1*cosecα*cos(2γ＋α)+r1*{-c*cos2β+r2cotβ}-b*(r1+r2)*cos2γ

=r2*	h-r1*cosecα*sin(2γ＋α)+r1 r2*r1*cosecα*cos(2γ＋α)+r1*{-h*cot2β+r2cotβ}-h*(r1+r2)*cot2γ

=ｍ

直線ASと直線BTの交点のｘ座標の満たす式は

ｋｘ　+　c*sin2β＝ｌｘ+ｌ*c*cos2β

ｘ=

ｌ*c*cos2β-c*sin2β ｋ-ｌ

=h*

ｌ*cot2β-1 ｋ-ｌ

(１)

直線ASと直線CUの交点のｘ座標の満たす式は

ｋｘ+c*sin2β＝ｍx-ｍ*b*cos2γ

ｘ=

-c*sin2β-ｍ*b*cos2γ ｋ-ｍ

=h*

ｍ*cot2γ+1 ｍ-ｋ

(２)

(１)と(２)が等しいことを計算すればよい。

　『頂点と接点を結ぶと？』 へ

　数学の部屋へもどる