『正四面体の問題』解答

◆愛知県　Y.M.Ojisan さんからの解答。

【解答】

a3 90

【証明】

（記号の都合から内部の点はXとします。）

正四面体の底面の面積：S＝

4

a2

正四面体の体積：V＝

１２

a3＝

(p+q+r+s)*S 3

より

p+q+r+s＝

*aである。

ｐ、ｑ、ｒ、ｓを

*a＝H：正四面体の高さで規格化し、

これをP,Q,R,Sとする。

即ち　P+Q+R+S=1

またｐ、ｑ、ｒ、ｓの４！対称性からP≧Q≧R≧S≧０の制限下で
X(Q,R,S)の存在範囲の体積をｖとするとき、もとめる体積は　４！*ｖである。

なお、P,Q,R,S間の等号関係は体積に寄与しないので重複を無視した。

三角形である条件は最小２辺の和が最大長辺より長いことである。
P≧Q≧R≧S≧０の条件下ではこれは　P≦R＋Sに集約される。

これにP=1-Q-(R+S)を代入すればQ,R,Sに対する条件は

R+S≧１−Q-(R+S) Q≧R≧S≧０　である。

書き直すと

Q≧1-2(R+S) ,

1-(R+S) 2

≧Q , Q≧R≧S≧０

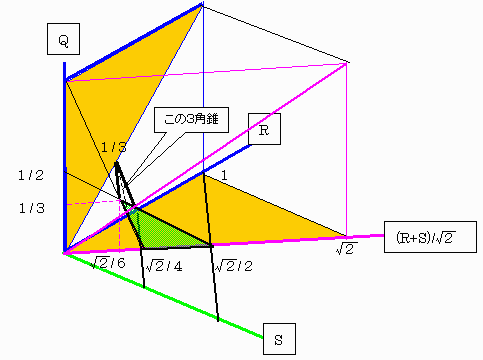
この条件を満たす領域は上図の「この３角錐」であって、その頂点の座標(P,Q,R,S)は

X1：(

1 4

,

1 4

,

1 4

,

1 4

)，x2：(

1 3

,

1 3

,

1 3

,0)

X3：(

1 3

,

1 3

,

1 6

,

1 6

)，x4：(

2 5

,

1 5

,

1 5

,

1 5

)である。

X1は４面体の重心、X2は面の中心、X3は面の中心と中心の中点、

X4はX１からP方向（４面体の頂点方向）へ(

2 5

-

1 4

)Hはなれた点である。

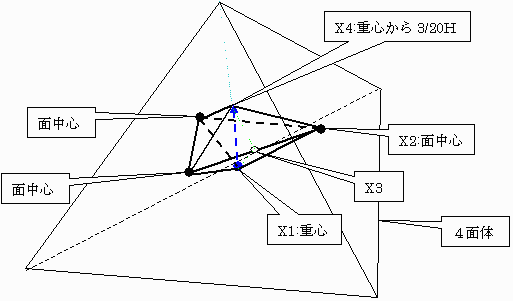
従って、Xの範囲は面の中心４点と、重心から各頂点の方に3/20Hはなれた点４個を頂点とする１２面体の内部である。

下図はそのうちPが最大の６ケースを合体させた全体の1/4の部分である６面体を図示したものである。

この形状の体積は、面中心を結んだ正三角形の面積を底面とし、高さ3/20Hの三角錐で計算できる。

よってXの体積４！*ｖは

{(

a 3

)

2

*

4

}*{

3 20

*

a

}/3*4

＝

a3 90

◆山梨県　Footmark さんからの解答。

ｐ,ｑ,ｒ,ｓのどの３つであっても、三角形ができるための条件は以下である。

・　ｐ,ｑ,ｒ,ｓのいずれも、負ではない。
・　ｐ,ｑ,ｒ,ｓのいずれも、他の任意の２つの合計以下である。

（ただし、辺長０や２辺の和が１辺と等しいばあいも、潰れてはいるが広い意味で三角形とした。）

つまり、ｐについて示すと、

０≦ｐ≦ｑ＋ｒ
０≦ｐ≦ｒ＋ｓ
０≦ｐ≦ｓ＋ｑ

∴　０≦３ｐ≦２(ｑ＋ｒ＋ｓ)

一方、与えられた正四面体の高さをｈとすると、

ｈ＝ｐ＋ｑ＋ｒ＋ｓ

∴　０≦ｐ≦

２ ５

ｈ

ｑ,ｒ,ｓにおいても同様なことがいえるので、

０≦ｑ≦

２ ５

ｈ , ０≦ｒ≦

２ ５

ｈ , ０≦ｓ≦

２ ５

ｈ

つまり、条件を満たすためには、点Ｐは与えられた正四面体の各面から、

２ ５	ｈ以下の距離でなければならない。

そこで、条件を満たさない、高さ

３ ５

ｈの正四面体を、

各頂点からそれぞれ切り取るものとする。

すると、下図のように

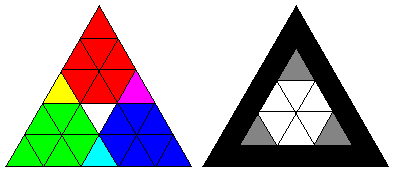
辺長が

１ ５

ａの正三角形(白)が各面に１つずつ残り、

辺長が

１ ５

ａの正六角形(白)が各切り口面に１つずつ残る。

ところが、これらの面(白い部分)上のどの点も条件を満たすわけではない。
条件を満たすのは、その中心の１点だけである。

何故なら、各面に残った正三角形(白)では、内部にあるどの点も、その面からの距離は０である。
それ故、他の任意な二面からの距離は常に等しくならなければならない。
それを満たす点は中心点だけであることは、明らかである。

また、各切り口面に残った正六角形(白)では、

内部にあるどの点も、対する底面からの距離は

２ ５

ｈである。

ところが、他のどの面からの距離も

２ ５

ｈ以下である。

それ故、他の任意な二面からの距離の和は常に

２ ５	ｈ以上にならなければならない。

それを満たす点は中心点(任意２距離の和が常に

２ ５

ｈ)

だけであることは、上の右図からも明らかである。

つまるところ、点Ｐが条件を満たす領域は、ここで示した４つの各面の中心点と４つの各切り口面の中心点との計８点を、すべての頂点とする１２面体の内部になる。

そこで、その１２面体だが、より想像しやすいように表現すると以下となる。

与えられた正四面体の各面の中心点を線で結ぶと内部に新たな正四面体ができるが、
できた正四面体の各面に、各面を底面とし頂点が底面の中心の真上にある等しい三角錐を付け加えた１２面体である。

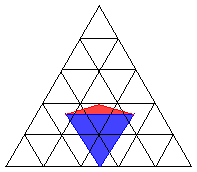
（上図は、三角錐(赤)を付け加えたようすを、新たな正四面体(青)の１面に限って示したものである。）

その三角錘の高さが(

２ ５

−

１ ３

)ｈであることは次のように容易に理解できる。

新たな正四面体は、元の正四面体に逆さまに内接するため、
新頂点が元の底面の中心点に接し、新底面は元の底面から、新たな正四面体の高さだけ離れている。

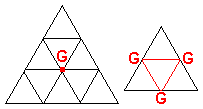
ところで、新たな正四面体の１辺の長さは、上図からも明らかのように、

１ ３

ａである。

それ故、新たな正四面体(青)の高さは明らかに

１ ３

ｈであり、

各三角錐(赤)の高さは(

２ ５

−

１ ３

)ｈである。

よって、与えられた正四面体の体積を Ｖ とすると、

条件を満たす領域の体積＝{(

１ ３

)

3

＋４(

１ ３

)

2

(

２ ５

−

１ ３

)}Ｖ＝

１ １５

Ｖ

ところで、Ｖ＝

１２

ａ3。

∴　条件を満たす領域の体積＝(

１ １５

)(

１２

)ａ

3

＝

１８０

ａ3

【答え】

１８０

ａ3

　『正四面体の問題』へ

　数学の部屋へもどる