
仧垽抦導丂Y.M.Ojisan 偝傫偐傜偺夝摎丅
亂栤戣侾亃
| f(n)=[ | n 3 |
]*[ | n+1 3 |
]*[ | n+2 3 |
]丆 [ ]:僈僂僗婰崋 |
佹堦杮捈慄傪堷偒傑偡丅
側傞傋偔偨偔偝傫惓嶰妏宍傪嶌傞偵偼丄屻偺捈慄偼偙偺捈慄偵懳偟丄0搙丄120搙丄亅120搙偺偄偢傟偐偺孹偒傪帩偮傋偒偱偡丅
傛偭偰値杮傪俁慻偵暘偗偦偺愊偑嵟戝偵側傞傛偆偵偡傟偽傛偄丅
| 偮傑傝丄傎傏摨抣偺[ | n 3 |
]丆[ | n+1 3 |
]丆[ | n+2 3 |
]偵暘偗傟偽傛偄丅 |
亂栤戣俀亃
俀杮偺慄偑廳側偭偨偲偒偼侾杮偺慄偲摨摍偲偟傑偡丅
傑偨値亞俁偲偟傑偡丅
嵟戝抣f(n)偺忬懺偐傜丂揔摉側慄堦杮傪暯峴側慄偺忋偵廳偹傟偽
f(n-1)偵掅尭偱偒傞偺偱f(n-1)+1乣f(n)-1杮偑壜擻偱偁傟偽悢妛揑婣擺朄偵傛傝壜擻偱偡丅
側偍丄f(3)=侾乮偺傒乯偱偁傞偐傜n=3偵偍偄偰惉棫偟偰偄傑偡丅
[戝嶨攃側徹柧]
n=6m偲偟傑偡丅
f(n)=8m3 丆f(n-1)=8m3-4m2
偱偁傞偺偱丂f(n)傪儀乕僗偵侾偐傜4m2傑偱嶍尭偱偒傟偽廫暘偱偡丅
嵟弶偵壓恾偺崟慄偲嬻怓慄偱帵偝傟傞傛偆偵鉟楉偵暲傋傞丅
侾杮尭傜偡偵偼嬻怓慄偺堦杮傪乽1乿偱帵偝傟傞慄偺埵抲偵堏摦偟傑偡丅
俀杮偺帪偼乽2乿偱帵偝傟傞慄偺埵抲偵堏摦偟傑偡丅
嵟弶偺慄偱嵟戝乽2m乿嶍尭壜擻偱偡丅
師偵傕偆堦杮嬻怓慄傪堏摦偟偰備偒傑偡丅
俀杮栚俁杮栚偼嵟戝乽2m-1乿嶍尭偱偒傑偡丅
嵟屻偺m杮栚偼乽m乿嶍尭偝傟丄偙偺庤弴偵傛傝丄1偐傜3m2杮傑偱慡偰嶍尭壜擻偱偡偑 4m2偵偼晄懌偱偡丅
偦偙偱儀乕僗傪8m3-2.8m2偖傜偄偵尭傜偡偙偲傪峫偊傑偡丅
(2.8偵怺偄堄枴偼柍偄丅3傛傝彮偟彮側偄偩偗)

偡側傢偪丂2m*(2m-k)*(2m+k)佮 8m3-2.8m2傛傝
k=Ceiling(1.183併倣) 偲偡傞丅
壓恾偵帵偡傛偆偵偙偺応崌傕傎傏3m2嶍尭壜擻偱偁傝丄2m2偼廫暘嶍尭偱偒傞丅
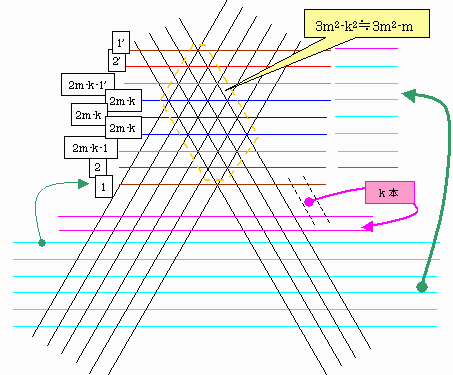
m偑戝偒偔側傟偽丄併偺愗傝幪偰傗丄n偑6m偱側偄偙偲偺塭嬁偼憡懳揑偵彫偝偔側傝丄戝嶨攃側徹柧偱廫暘偱偁傞丅
栤戣偼値偑彫偝偄帪偱偁傝丄桳尷側偺偱屄暿偵挷傋傟偽偱偒傞偱偟傚偆丅
[倣倣偲偟偨徹柧]丂
n=a+b+c偵暘偗傜傟偰偄傞偲偒丄g(a,b,c)=a*b*c偐傜偳傟偩偗岎揰偵廳偹傞曽朄偱惓嶰妏宍傪尭傜偣傞偐偲偄偆偲丄
| d(a,b,c)=[a*b+b*c+c*a+ | 1 4 |
-( | n 2 |
) | 2 | ]偱偡丅 |
偨偩偟偙偺幃偼丂a+b亞c & a+c亞b & b+c亞a 乮嶰妏宍偺俁曈乯偺偲偒偵尷傝傑偡丅
扨弮偵寁嶼偡傟偽弌偰偒傑偡偺偱徹柧棯丅
[丂]傪梡偄側偄偲丄d(a,b,c)偼n偺嬼婏惈偱丄f(n)偼丂n mod 3 偺抣偱庒姳昞幃偑堎側傞偺偱 n mod 6偱暘椶偟偰峫偊傞昁梫偑偁傝傑偡偑丄
1/4傪偼偢偟偰
| d(a,b,c)亞(a*b+b*c+c*a-( | n 2 |
) | 2 | )=兿(a,b,c)偱峫偊,n mod 3 偱暘椶偟傑偡丅 |
懄偪 f(n)=g(m,m,m+p) 丆n=3m+p丆p=-1 or 0 or 1 傪嵟弶偺忬懺偲偟傑偡丅
傕偟丄f(n)-d(m,m,m+p)亝f(n)-兿(m,m,m+p)亝1+f(n-1) 偱偁傟偽徹柧廔傢傝偱偡丅
偟偐偟偦偆偱偼側偄偺偱 a=m 偐傜1杮 b=m傊堏摦偝偣a=m-1,b=m+1偵偟傑偡丅
偙偺偲偒丂
f(n)=g(m,m,m+p)-兿(m,m,m+p)亝1+g(m+1,m-1,m+p)偱偁傟偽
g(m+1,m-1,m+p)傑偱弴師嶍尭偱偒偰丄
g(m+1,m-1,m+p)-兿(m+1,m-1,m+p)亝1+f(n-1)偱偁傟偽徹柧廔傢傝偱偡丅
偩傔側傜傕偆堦杮偲偄偆偙偲偱堦斒偵
g(m+k,m-k,m+p)-兿(m+k,m-k,m+p)亝1+g(m+1+k,m-1-k,m+p) ---(1) 傑偨偼
g(m+k,m-k,m+p)-兿(m+k,m-k,m+p)亝1+f(n-1) ----(2)
偑k=0偐傜(2)偑惉棫偡傞k傑偱偺娫偱惉棫偟偰偄傟偽傛偄丅
彮偟夞傝偔偳偄偱偡偑丄偦傟偼偙偺忦審傪丄椉幃(1)(2)偺壛嶼偱偁傞壓婰娭學幃(3)偺惉斲偱戝傑偐偵敾掕偡傞曽朄傪偲傞偨傔偱偡丅
g(m+1+k,m-1-k,m+p)+f(n-1)+2(1+兿(m+k,m-k,m+p)- g(m+k,m-k,m+p))亞侽
亙p=-1偺応崌亜
偙偺応崌f(n-1)=g(m-1,m-1,m)偱偡丅
m=5+q偲偟偰寁嶼偡傞偲(3)嵍曈偼壓婰偱偡丅
(壓懯抣5偼幚偼摎偊傪抦偭偰弌傞抣偱偡丅懠傕摨條)
| (2+q)(k- | 4+q 2+q |
) | 2 | + | q3+8q2+20q+8 2q+4 |
偙偺幃偼q亞0偵偍偄偰惓偱偡丅
懄偪3m-1偺宯摑偱偼n=14埲忋偼俷俲偱偡丅
亙p=0偺応崌亜
偙偺応崌f(n-1)=g(m,m,m-1)偱偡丅
m=5+q偲偟偰寁嶼偡傞偲(3)嵍曈偼壓婰偱偡丅
| (3+q)(k- | q+5 3+q |
) | 2 | + | q3+9q2+23q+7 2q+6 |
偙偺幃偼q亞0偵偍偄偰惓偱偡丅
懄偪3m偺宯摑偱偼n=15埲忋偼俷俲偱偡丅
亙p=1偺応崌亜
偙偺応崌f(n-1)=g(m,m,m)偱偡丅
m=4+q偲偟偰寁嶼偡傞偲(3)嵍曈偼壓婰偱偡丅
| (3+q)(k- | q+5 3+q |
) | 2 | + | q3+9q2+21q+1 2q+6 |
偙偺幃偼q亞0偵偍偄偰惓偱偡丅
懄偪3m+1偺宯摑偱偼n=13埲忋偼俷俲偱偡丅
k偼偣偄偤偄 [併(n/3)] 偱偡偐傜丄値亞13偱偼兿偺堷悢a,b,c偵梫媮偝傟傞俁妏宍偺娭學偼枮懌偝傟偰偄傑偡丅
埲忋傛傝丂値亞13丂埲忋偱偼壜擻偱偁傞偙偲偑徹柧偝傟傑偟偨丅
亙値亙13丂偺応崌偵偮偄偰嬶懱揑偵挷傋傑偡丅亜
| m=[ | n+1 3 |
] | 丆 p=n-3m丆f(n)=m3+pm2丆k=[併( | d(m,m,m+p)+1 m+p |
)]偲偟偰丄 |
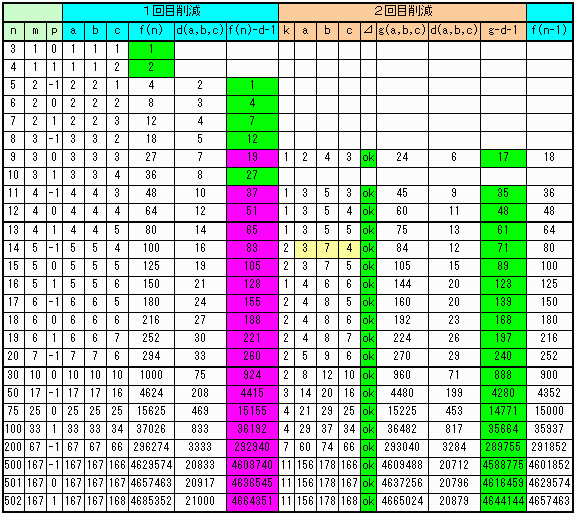
壓昞偵帵偡傛偆偵n=3,4偼偦偺傑傑偱惉棫丅
n=5,6,7,8,10偼侾夞栚偺嶍尭偱惉棫丅
n=9,11,12偼侾杮偺堏摦傪侾夞峴偄丄俀夞栚偺嶍尭偱惉棫偟偰偄傞丅
埲忋偱徹柧姰椆丅
乷側偍丄n=12偼偓傝偓傝撏偄偨偲偄偆偲偙傠偱偡偑丄a,b,c傪4,4,4偐傜3,3,6偵堏摦偝偣傟偽
g=54,d=9,g-d-1=44偱傜偔傜偔摓払偟傑偡丅乸
崌傢偣偰丄n=13埲崀傕堦晹壓昞偵帵偟傑偟偨丅
俀夞傑偱偵摓払偟偰偄傑偡丅
亂姶憐亃
戝嶨攃側徹柧傑偱偼梕堈偱偟偨偑丄偒偭偪傝偟偨徹柧偺曽偼傗傗偙偟偔偰旀傟偨丅
偳偆偣俤倃俠俤俴偱壓偺傎偆傪寁嶼偟偨偺偱丄傕偭偲戝傑偐側徹柧偱傕傛偐偭偨丅
亂偍傑偗亃
(a) 惓嶰妏宍偺撪晹偲捈慄偑岎傢傜側偄傕偺偺傒傪偐偧偊偨応崌
亂偍傑偗a栤戣1亃
| f(n)=[pm- | p2 2 |
+ | 3m2 2 |
] |
| 偙偙偱m=[ | n+1 3 |
] , p=n-3m丂, [丂]:愗傝幪偰 |
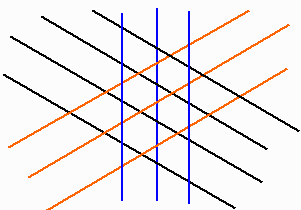
佹摨條偵捈慄傪0搙,120搙,-120搙偺俁僌儖乕僾偵暘偗偦傟偧傟a,b,c偲偡傞丅
a偐傜侾杮乮惵慄乯傪帩偭偰偒偰丄b偲們慡晹傪巊偭偰嵟戝壗屄惓俁妏宍偑嶌傟傞偐峫偊傞偲丄
壓恾偺傛偆偵b=c偱偼丂b+c-1偱偁傞丅
傑偨b亜c側傜2c偱偁傞丅

偟偨偑偭偰丄b偲們偱偱偒傞奿巕揰娫偵丄側傞傋偔a曽岦偺懳妏慄偵嬤偄傎偆偐傜a偺慄傪嵎偟崬傫偱峴偔偺偑嵟戝屄悢偺惓嶰妏宍傪偁偨偊傞丅
偦偺悢偼丄娭傢傞b偲們偺岎揰偺俀攞掱搙偵側傞偐傜丄慜偺栤戣偺倓偺傎傏俀攞偱偁傞偙偲偑傢偐傞丅
幚嵺偵寁嶼偡傞偲丄
| f(a,b,c)=[2*(ab+bc+ca)- | n2 2 |
] 丆n=a+b+c 偱偁傞丅 |
偙偺抣偑嵟戝偵側傞偺偼a=b=c偺偲偒偱偁傞丅
| 廬偭偰値偑俁偺攞悢偺偲偒偼a=b=c= | n 3 |
| n mod 3=1偺偲偒偼丂a=b= | n-1 3 |
丆c=a+1 |
| n mod 3=2偺偲偒偼 a=b= | n+1 3 |
丆c=a-1 偑嵟戝抣傪梌偊傞丅 |
偙傟傪彂偒姺偊傞偲夝摎偱偁傞丅
亂偍傑偗a栤戣俀亃
偙偪傜偼梕堈偵壜擻偱偁傞丅
庤弴偺堦偮傪n=12偺応崌偵偮偄偰壓恾偵帵偡丅
懠偵傕曽朄偼偁傞偑丄gif傾僯儊偺僼傽僀儖埑弅棪偑崅偄偲巚傢傟傞傕偺傪嵦梡偟偨丅
f(12)=24偱偡丅
偙偺曽朄偺億僀儞僩偼侾杮乮愒慄乯偩偗惍楍偝偣側偄偲偙傠偱偁傞丅

仧弌戣幰偺僐儊儞僩丅
Y.M.Ojisan 偝傫夝摎偁傝偑偲偆偛偞偄傑偡丅
亂栤戣侾亃惓夝偱偡丅
亂栤戣俀亃嵶偐偄寁嶼埲奜偼妋擣偟傑偟偨丅
偐側傝椙偄昡壙傪偝傟偰偄偰尒帠偱偡丅
乮巹偺梡堄偟偰偄偨夝摎偱偼n亞55偲偐側傝昡壙偑峳偄偱偡丅乯
埲壓偼幹懌偱偡偑丄巚偭偨偙偲偱偡丅
[戝嶨攃側徹柧]偱偼俀夞偺嶍尭偱嵪傑偣偰偄傑偡偑丄[倣倣偲偟偨徹柧]偱偼壗夞傕嶍尭傪峴偭偰偄傑偡偹丅
偙偪傜偺曽偑惛枾偱偡偑丄[戝嶨攃側徹柧]偺曽恓偱
k = [併(n/6)]
偲偟偨曽偑懡彮寁嶼偑妝偐傕抦傟傑偣傫丅
乮偪傖傫偲寁嶼偟偰傑偣傫偑乯
亜偒偭偪傝偟偨徹柧偺曽偼傗傗偙偟偔偰旀傟偨丅
巹傕丄帺暘側傝偵徹柧偟偰偐傜弌戣偟傛偆偲偟偨偺偱旀傟傑偟偨丅
偁偲丄敪尒揑側曽朄偵傛傞夝摎傕婜懸偟偰偄傑偡偑丄偙偪傜偼擄偟偄偐傕偟傟傑偣傫丅
亂偍傑偗a栤戣1亃
懡暘惓夝偱偟傚偆丅
偲偄偆偺傕丄巹偼偙傟傪徹柧偱偒偰偄傑偣傫丅
偙偺徹柧偺栤戣揰偼丄b偲c偱偱偒傞奿巕偵侾杮偢偮捈慄傪壛偊偰偄偔乽奺抜奒乿偱惓嶰妏宍傪嵟戝偺屄悢嶌偭偨偲偟偰
傕丄偦傟偑乽慡懱乿偱惓嶰妏宍偑嶌傟傞嵟戝屄悢偩偲偄偆偙偲偼帺柧偱偼側偄丄偲偄偆強偱偡丅
側偺偱丄傕偆彮偟愢柧偑昁梫偩偲巚偄傑偡丅
亂偍傑偗a栤戣俀亃
栤戣侾偑惓偟偗傟偽惓夝偱偡丅
傾僯儊乕僔儑儞偑暘偐傝傗偡偔偰偽偭偪傝偱偡乮丱丱
仧垽抦導丂Y.M.Ojisan 偝傫偐傜偺夝摎丅
亂偍傑偗a侾亃
屼巜揈屼栟傕丅昅椡尷奅偵偰徣棯屼柶丅昅椡夞暅壓婰徻弎丅
佹 a,b,c偼嶰妏宍偺3曈偺娭學偵偁傝b亞c偲偟傑偡丅
b偲們偺岎揰偺廤崌傪T偲偟傑偡丅
嶌恾偺搒崌忋a偼忋壓曽岦偲偟傑偡丅
側偍丄n=a+b+c偱偡丅
丂惓嶰妏宍偑俁曈偱峔惉偝傟傞偺偱偼側偔丄侾曈(伕a)偲侾揰(伕T)偱婯掕偝傟傞偲峫偊傑偡丅
忦審傛傝丄侾曈偲侾揰偺娫偵懠偺曈伕a偼擖傝偙傔傑偣傫丅
傑偨丄惓嶰妏宍撪晹偍傛傃曈忋偵懠偺揰伕T傕懚嵼偟摼傑偣傫丅
乮摨堦揰忋偺俀揰偼侾揰偲傒側偡偺偱丄偨偔偝傫嶌傞応崌揰偼慡晹堎側傞偲峫偊偰椙偔丄惓俁妏宍捀揰忋傪摿偵彍奜偟偰偄側偄丅乯
丂懄偪丄侾揰伕T偵偮偒丄a偼侾揰偺嵍塃偺俀杮偺傒偑惓嶰妏宍惗惉偵桳岠偱偡丅
乮幹懌丗傛偭偰惓嶰妏宍屄悢偑2bc埲壓偱偁傞偙偲偼妋幚乯
丂埲忋偐傜丄a偵捈岎偡傞曽岦偵嫮扨挷憹壛側倫屄偺揰楍t倫伕T丂傪峫偊傞偲偒丄
a偲t倫偱嶌惉壜擻側惓嶰妏宍偺嵟戝悢偼a偲t倫偑岎屳偵暲傇応崌偱偁偭偰偦偺悢偼
a亜倫偺応崌丂2倫, a亖倫偺応崌丂2a-1, a亙倫偺応崌丂2a
偱偁傞偲尵偊傑偡丅
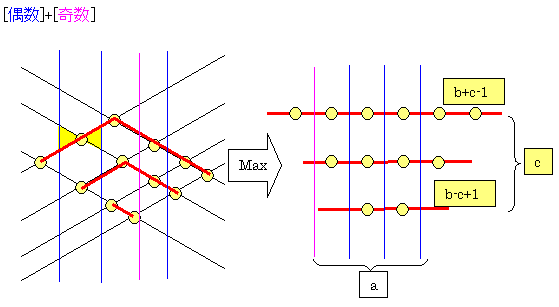
丂t倫偲偟偰壓恾愒慄忋偺們慻偺揰楍偺廤崌傪峫偊傑偡丅
倫亖b-c+1 , b-c+3丂丏丏b+c-1 偱偡丅
偙傟傜偼a偵捈岎偡傞曽岦偵嫮扨挷憹壛偲偄偆忦審傪枮懌偟偰偄傑偡丅
丂傛偭偰惓嶰妏宍偺嵟戝悢偼壓婰幃埲壓偲側傝傑偡丅
X偼a=b-c+2I-1偑惉棫偟偨悢偱侽偐侾偱偡丅
嬶懱揑偵偼2I=a-b+c+1=(n+1)-2b側偺偱丂n偑婏悢偺帪侾丂嬼悢偺帪侽偱偡丅
| 們 嚁 I=1 |
2*Min(a,b-c+2I-1)亅X |
[嬼悢帪]
| I=1乣 | n 2 |
-b丂偱偺嚁偼 |
| (b-c+1+b-c+n-2b-1)( | n 2 |
-b)=(n-2c)( | n 2 |
-b) |
| I= | n 2 |
-b亄1乣們偱偺嚁偼2a(c- | n 2 |
+b) |
埲忋傪崌嶼偡傞偲
| n2 2 |
-nc-nb+2bc+2ac-na+2ab=2(ab+bc+ca)- | n2 2 |
[婏悢帪]
| I=1乣 | n+1 2 |
-b丂偱偺嚁偼 |
| (b-c+1+b-c+n+1-2b-1)( | n+1 2 |
-b)=(s-2c)( | s 2 |
-b) |
| I= | n+1 2 |
-b亄1乣們偱偺嚁偼2a(c- | s 2 |
+b) |
埲忋傪崌嶼偡傞偲
| s2 2 |
-sc-sb+2bc+2ac-sa+2ab-1 |
| =2(ab+bc+ca)+ | s(s-2n) 2 |
-1 |
| =2(ab+bc+ca)- | n2 2 |
- | 1 2 |
| 傑偲傔偰[2(ab+bc+ca)- | n2 2 |
] 偱偁傝丄 |
傑偨幚嵺丄慜夞夝摎偺曽朄偱偦偺傛偆側a傪嶌恾壜擻偱偡丅
側偍丄a,b,c偑嶰妏宍偺3曈偺娭學偵側偄応崌(a亞b+c)偼a偑梋傝偩偡偺偱丄嵟戝偵側傞偙偲偼偁傝傑偣傫丅
仧弌戣幰偺僐儊儞僩丅
Y.M.Ojisan 偝傫嵞傃夝摎偁傝偑偲偆偛偞偄傑偡丅
亂偍傑偗a侾亃
崱搙偼妋幚偵惓夝偱偡丅 側傞傎偳丄墶偺愜傟慄偼尒偊傑偣傫偱偟偨丅幚偵擺摼偑偄偒傑偟偨丅
堦売強偩偗昞尰偵拲暥傪晅偗偝偣偰栣偄傑偡偲丄
亜丂埲忋偐傜丄a偵捈岎偡傞曽岦偵嫮扨挷憹壛側倫屄偺揰楍t倫伕T丂傪峫偊傞偲偒
偙偙偼丄揰楍t倫偺乮a偵捈岎偡傞曽岦乯偵椬傝崌偆俀揰傪寢傇慄暘偼丄捈慄懓b枖偼c乮偺堦晹乯偵娷傑傟偰偄側偗傟偽偄偗側偄丄偲偄偆傛偆側偙偲偑堦尵偼昁梫偱偡偹丅
恾偱偼偦偆側偭偰偄傞偺偱徹柧偵栤戣偼偁傝傑偣傫偑丅
仧垽抦導丂Y.M.Ojisan 偝傫偐傜偺僐儊儞僩丅
亂偍傑偗a侾 Reply亃
亜偲偄偆傛偆側偙偲偑堦尵偼昁梫偱偡偹丅
偝偡偑尩枾偱偡偹丅偛巜揈偺忦審偑昁梫偱偡丅埫栙抦偵側偭偰偄傑偟偨丅
帺暘偱彂偄偰偍偒側偑傜偱偡偑丄師偺暥傕昁慠惈偵娭偟暔尵偄偑晅偒偦偆偱偡丅
亜丂t倫偲偟偰壓恾愒慄忋偺們慻偺揰楍偺廤崌傪峫偊傑偡丅
夝愢丗俿偺揰傪桳岠偵巊梡偡傞偵偼p亙a偱偁傞偙偲偑朷傑偟偄偺偱偡偑丅
嵟弶偼偳偆偟偰傕倫亖倐亄們亅侾亞倎偺揰楍偑偁傞応崌偑偁偭偰偦偺晹暘偼幪偰偞傞傪摼側偄丅
埲屻嵟挿偺揰楍傪嵦梡偟偰備偔偲丄恾偺們慻偵側傞傢偗偱偡丅