◆東京都 哲(サトシ) さんからの解答。
(1)
| S= | r(AB+BC+CA) 2 |
より、S_6= | R(AB+BC+CA) 2 |
= | RS r |
。 |
(2)
∠BOC=α, ∠COA=β, ∠AOB=γ とおくと、
| s=R(sin( | α 2 |
)+sin( | β 2 |
)+sin( | γ 2 |
)) |
| = | S_6 2 |
| = | RS 2r | 。 |
◆山梨県 Footmark さんからの解答。
(1)
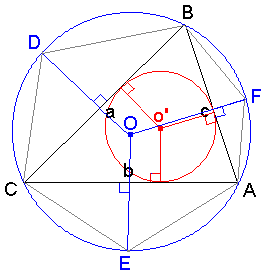
外接円の中心を O、3辺 BC , CA , AB のそれぞれの長さを a , b , c とすると、
求める面積S_6は3つの四角形 OBDC , OCEA , OAFB の面積の和である。

いずれの四角形も、2本の対角線は直交し長さRの対角線を1本ずつ持つが、残りの対角線の長さはそれぞれ a , b , c である。
| ∴ S_6= | R(a+b+c) 2 |
| ∴ S= | r(a+b+c) 2 |
| ∴ | a+b+c 2 |
= | S r |
| S_6=S* | R r |
| 【答え】 S_6=S* | R r |
◆山梨県 Footmark さんからの解答。
(2)
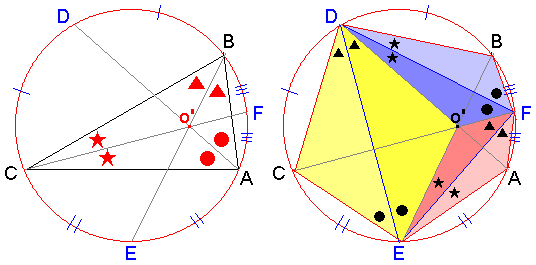
左図のように、線分 AD,BE,CF を引くと、3つ線分は△ABCの3頂角をそれぞれ2等分する。
(何故なら、同一円において弧長が等しければ、張る円周角も当然等しい。)
線分 AD,BE,CF が△ABCの各頂角の2等分線ならば、3線分は1点o'(△ABCの内心)で交わる筈である。
すると、右図より明らかに、2角と挟辺が等しいため
△EAF≡△Eo'F ,
△FBD≡△Fo'D ,
△DCE≡△Do'E 。
よって、求める三角形DEFの面積は六角形AFBDCEの面積の半分である。
| (1)より、六角形AFBDCEの面積は S* | R r |
| 故に、求める面積は | SR 2r |
。 |
| 【答え】 | SR 2r |
◆出題者のコメント
哲(サトシ)さんの(2)の解答は答はあっているのですが、
| s=R(sin( | α 2 |
)+sin( | β 2 |
)+sin( | γ 2 |
)) |
Footmarkさんの解答(1,2)は出題者と同じ解き方でした。
◆東京都 哲(サトシ) さんからの解答。
(2)
△ABCの外接円の中心を O とおき、
∠BOC=α, ∠COA=β, ∠AOB=γ とおくと、
s = △DOE+△EOF+△FOD
| = R | 2 | sin( | α 2 |
+ | β 2 |
)/2+R | 2 | sin( | β 2 | + | γ 2 |
)/2+R | 2 | sin( | γ 2 | + | α 2 |
)/2 |
| = R | 2 | sin(π-( | α 2 |
+ | β 2 |
))/2+R | 2 | sin(π-( | β 2 | + | γ 2 |
))/2+R | 2 | sin(π-( | γ 2 | + | α 2 |
))/2 |
| = R | 2 | sin( | γ 2 |
)/2+R | 2 | sin( | α 2 |
)/2+R | 2 | sin( | β 2 |
)/2 |
| = △AOF+△BOD+△COE |
| = △FOB+△DOC+△EOA |
ここで、
△AOF+△BOD+△COE+△FOB+△DOC+△EOA=S_6
であるから、
| s= | S_6 2 | = | RS 2r | ...(答) |
◆出題者のコメント
(2)は内接円の中心と外接円の中心のどちらに注目するかで難易度が大分違うようですね。
△DOE, △AOF, △BOFの面積が同じだとは気がつきませんでした。
(3)は(1)や(2)のように簡単にはいかないので、やり応えがあると思います。