◆静岡県 ヨッシー さんからの解答。
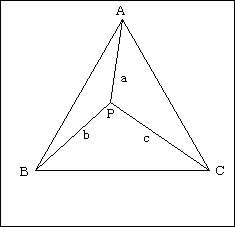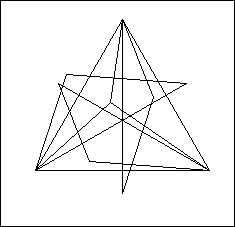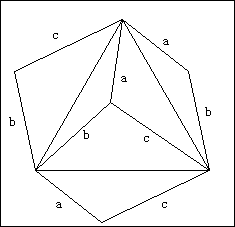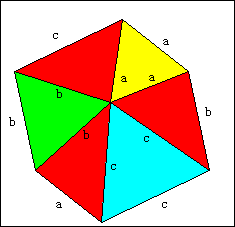
図のように、△ABP、△BCP、△CAPを60度回転すると、
△ABCの2倍の面積をもつ六角形ができます。

この六角形は、一辺がa、b、cの3種類の正三角形1つずつと、3辺が、a、b、cの三角形3つに分けることができます。
1辺がaの正三角形の面積は、
| 1 ― 2 | × a × a × sin60°= |  4 | a2 |
同様にして、3つの正三角形の面積の和は、
 4 | (a2+b2+c2)= |  4 | ×p |
3辺がa、b、cの三角形の面積は、ヘロンの公式より、
![]()
変形して、
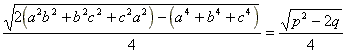
以上より、六角形の面積は
![]()
よって、△ABCの面積は、その半分で、
![]()
◆静岡県 村松 芳子 さんからの解答。
△ABPをABで折り返し、△ADBとする。
△BCP、ACPも、それぞれBC、ACで折り返し、△BEC、△CFAとする。
△ABC
=△ADB+△BEC+△CFA
=六角形ADBECFの面積の1/2
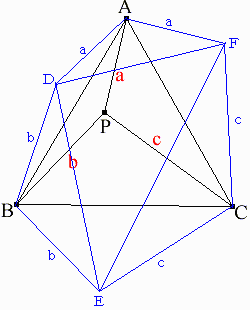
△ADB、△BEC、△CFA は いずれも 頂角120°、両底角30°の正三角形である。
DF=a
DE=b
EF=c が求まるので
が求まるので
| △ADF= |  4 | a2 |
| △BDE= |  4 | b2 |
| △CEF= |  4 | c2 |
△DEFは、ヘロンの公式に代入して
![]()
これを変形し、p、qで書き換えると、
![]()
となる。
△ADB+△BEC+△CFA
| = |  4 | (a2+b2+c2) |
| = |  4 | p |
ゆえに
![]()
(終わり)
最初の問題と同じ方法で解きました。
計算が大変でした。
◆静岡県 村松 芳子 さんからの解答。
△ABPをABで折り返し、△ADBとする。
△BCP、△ACPもそれぞれBC、ACで折り返し、△BEC、△CFAとする。
△ABC
=△ADB+△BEC+△CFA
=六角形ADBECFの面積の1/2
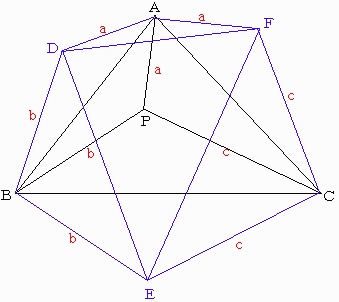
∠DAF=2α、∠DBE=2β、∠ECF=2γ
DF=2a sin α=x
DE=2b sin β=y
EF=2c sin γ=z
とおくと
| △ADB= | a2 sin 2α
2 |
| △BEC= | b2 sin 2β
2 |
| △CEF= | c2 sin 2γ
2 |
ゆえに
| △ADF+△BDE+△CEF= | r
― 2 |
△DEFはヘロンの公式に代入して
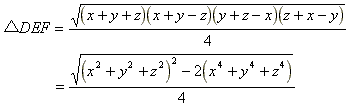
これを変形し、p,qで書き換えると
![]() となる。
となる。
ゆえに
![]()
最初の問題と同じ方法で解きました。
計算は慣れました。