亂偍傑偗亃
仧垽抦導丂Y.M.Ojisan 偝傫偐傜偺夝摎丅
亂摎偊亃
係俉亅侾俁併俁丂丂丂乮壓婰忬懺偱栺俀俆丏俆乯

亂偍傑偗亃
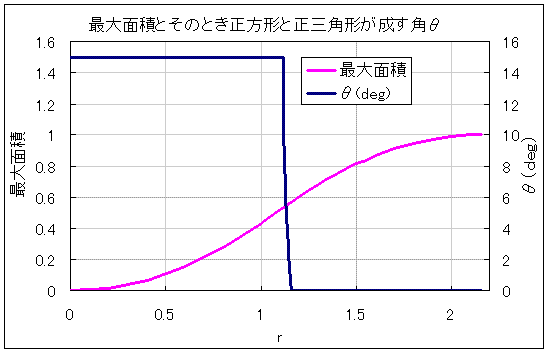
堦斒惈傪幐傢偢丄惓曽宍偺堦曈b偼侾偲偡傞丅
傑偨丄a/b亖倰偲偡傞丅
| 倰偺抣/斖埻 | 嵟戝柺愊乮倐俀乯 | 忬懺恾 |
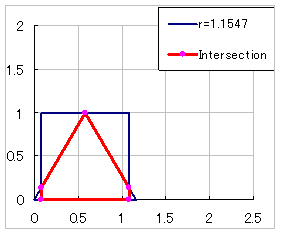
sec(15搙) 埲壓 |
倰俀亊併俁/係丗惓嶰妏宍偺柺愊 | 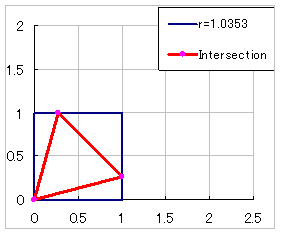 |
sec(15搙) 乣 乮俁併俀亅併俇乯 乗乗乗乗乗乗 俇 |
徻嵶偼壓婰 兤亖侾俆搙 |
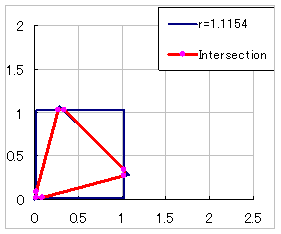 |
乮俁併俀亅併俇乯 乗乗乗乗乗乗 俇 乣 俀併俁 乗乗乗乗 俁 |
徻嵶偼壓婰 |
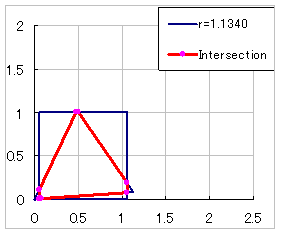 |
俀併俁 乗乗乗乗 俁 乣 侾亄俀/併俁 |
徻嵶偼壓婰 兤亖侽搙 |
 |
侾亄俀/併俁 埲忋 |
侾丗惓曽宍偺柺愊 | 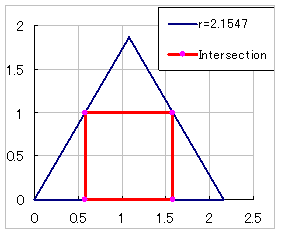 |
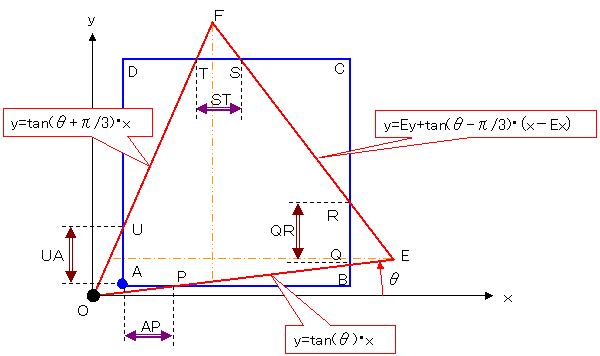
tan(兤)亖 |
E倷 乗 E倶 |
tan(兤-兾/3)亖 |
Ey亅併俁丒E倶 乗乗乗乗乗乗 E倶亄併俁丒Ey |
倲an(兤+兾/3)亖 |
Ey亄併俁丒E倶 乗乗乗乗乗乗 E倶亅併俁丒Ey |
| 揰 | 倶嵗昗 | 倷嵗昗 |
| A | Ax | Ay |
| B | Ax+1 | Ay |
| C | Ax+1 | Ay+1 |
| D | Ax | Ay+1 |
| E | Ex | Ey |
| F | 棯 | 棯 |
| P | Ay/tan(兤) | Ay |
| Q | Ax+1 | 乮Ax+1乯亊tan(兤) |
| R | Ax+1 | Ey+tan(兤-兾/3)iAx亄侾亅Ex乯 |
| S | Ex+乮A倷亄侾亅E倷乯/ tan(兤-兾/3) | Ay+1 |
| T | 乮Ay+1乯/tan(兤亄兾/3) | Ay+1 |
| U | Ax | tan(兤亄兾/3)丒Ax |
| 乷俁Ex俁-俁Ex俀亄乮併俁亅俀乯ExEy亄俁ExE倷俀-俀E倷俀乸乷Ex-併俁丒Ey乸 | |
| Ax= | 乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗 |
| 俀乷Ex俀亄E倷俀乸乷俁Ex亅併俁丒Ey乸 | |
| 丂 | |
| 乷乮俁亅俇併俁乯E倷俀亄俁併俁丒Ey俁亄乮俀併俁亅俇乯ExEy亄俋ExE倷俀亄俁併俁丒Ex俀E倷亄俋E倶俁亅乮俁亄係併俁乯E倶俀乸Ey | |
| A倷= | 乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗 |
| 俇乷Ex俀亄E倷俀乸乷Ex亄併俁丒Ey乸 |
| 乮俁E倶俀亅俁Ex亅俀併俁丒Ex亅併俁丒E倷亄俁E倷俀乯俀 | |
| F(Ex,Ey)= | 乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗 |
| 乷Ex亄併俁丒E倷乸乷俁Ex亅併俁丒Ey乸 |
| 倰乮侾亅倲俀乯 | |
| Ex= | 乗乗乗乗乗乗乗 |
| 乮侾亄倲俀乯 | |
| 丂 | |
| 俀倰倲 | |
| Ey= | 乗乗乗乗乗乗乗 |
| 乮侾亄倲俀乯 |
| 乷乮俁倰亄俁亄俀併俁乯倲俀亅俀併俁丒倲亄俁倰亅俁亅俀併俁乸俀 | |
| F(倲,倰)= | 乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗 |
| 乮俁倲俀亄俀併俁丒倲亅俁乯乮倲俀亅俀併俁丒倲亅侾乯 |
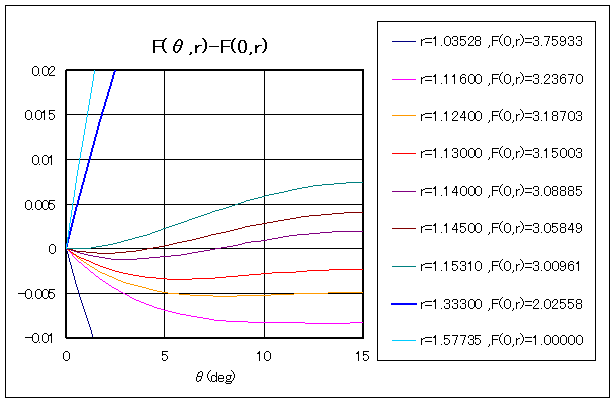
| F'(t,r)= | 亅4併俁 |
| 亊 | 乷乮俁倰亄俁亄俀併俁乯倲俀亅俀併俁丒倲亄俁倰亅俀併俁亅俁乸 |
| 亊 | 乷乮俁倰亄俀併俁乯倲俀亄乮俇併俁丒倰亄12r乯倲亅俁倰亄俀併俁乸 |
| 亊 | 乷倲俀亄乮俀併俁亄係乯倲亅侾乸 |
| 亐 | 乷乮倲亄併俁乯乮倲亄俀亅併俁乯乮倲亅俀亅併俁乯乮俁倲亅併俁乯乸俀 |
| 嬌抣傪梌偊傞丂倲 | |
| 乷侾乸 | 併俇亄併俀亅俀亅併俁丂丂乮栺侽丏侾俁俀乯 |
| 乷俀乸 | 乮俀併俁亅俁乯倰亅俀併乷乮俇亅俁併俁乯倰俀亅侾乸 乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗 併俁丒倰亄俀 |
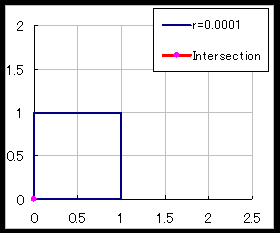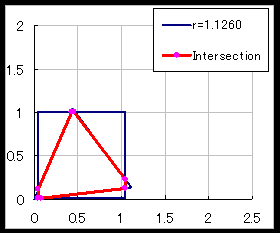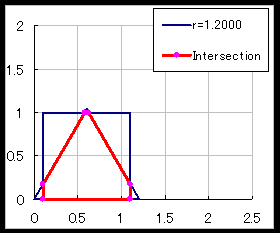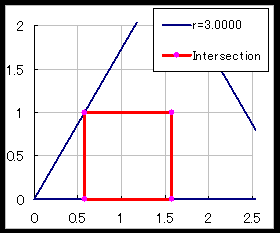
俥乮t,r乯偑旕忢偵鉟楉側幃偩偭偨偙偲傗丄旝暘偺0揰偑俀師幃偺夝偲偟偰摼傜傟傞偙偲偼嬃偒偱偟偨丅
偲偆偄偙偲偼丄婔壗妛揑偵傕偭偲娙扨側徹柧偑偁傞偲偄偆偙偲偱偟傚偆偹丅