x軸方向から見ると円、y軸およびz軸方向から見ると正方形である。
2方向から切断すると下図のような形になる。
x軸およびy軸方向から見ると円、z軸方向から見ると正方形である。

◆東京都 鳥居 さんからの解答。
1方向から切断すると円柱ができる。
x軸方向から見ると円、y軸およびz軸方向から見ると正方形である。
2方向から切断すると下図のような形になる。
x軸およびy軸方向から見ると円、z軸方向から見ると正方形である。

これは、y=sin x, y=−sin x (0≦x≦π) で囲まれる図形(下図)を4枚貼り合わせてできる。
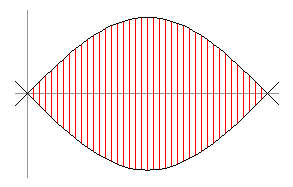
3方向から切断すると下図のような形になる。
x軸、y軸、z軸いずれから見ても円である。

これは、y=sin x, y=−sin x, y=cos x, y=−cos x (0≦x≦π/2) で囲まれる図形(下図)を12枚貼り合わせてできる。
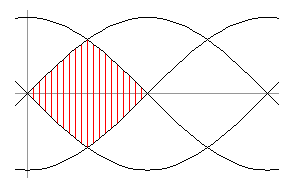
元の立方体の体積を1とするとき、上に出てきた立体の体積をまとめると以下のようになる。
| 立方体 | 1方向切断立体 | 2方向切断立体 | 3方向切断立体 | 球 |
| 1 (1.000) | π/4 (0.785) | 2/3 (0.667) | 2−√2 (0.586) | π/6 (0.524) |