◆東京都 Y.Mさんからの解答。
[問題] 正三角形の証明 ----- Morley(モーレー)の定理
ちなみに内角、外角、優角(内角の反対側の角)の3等分およびこれらの適当な組合せでも正三角形になります。
私は初等幾何学ではこれが1番美しい定理だと思っています
◆岐阜県 水の流れ さんからの解答。
Frank Morleyの定理
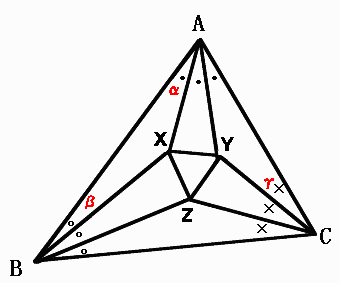
△ABCの∠A,∠B,∠Cの3等分線の、辺に近い2つずつの交点を図のようにX,Y,Zとする。
∠BAX=∠XAY=∠YAC=α
∠ABX=∠XBZ=∠ZBC=β
∠BCZ=∠ZCY=∠YCA=γとする。

△ABCの内角の和は180度だから、
3(α+β+γ)=180゜
∴α+β+γ=60゜
正三角形X'Y'Z'を作り、その外側にA',B',C'を
∠X'Y'A'=60゜+γ
∠Y'X'A'=60゜+β
∠Z'X'B'=60゜+α
∠X'Z'B'=60゜+γ
∠Y'Z'C'=60゜+β
∠Z'Y'C'=60゜+α のようにとる。
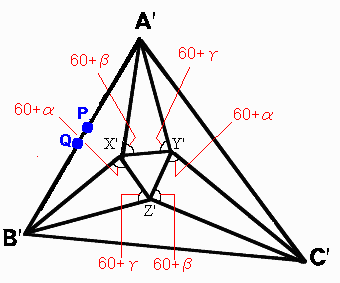
∠X'A'Y'
=180゜−∠X'Y'A'−∠Y'X'A'
=180゜−(60゜+γ)−(60゜+β)
=60゜−β−γ
=α
同様に、
∠X'B'Z'=β
∠Y'C'Z'=γである。
点Y',Z'のそれぞれA'X'、B'X'に関する対称点をそれぞれP,Qとすると
∠PX'Q
=360゜−2∠Y'X'A'−2∠Z'X'B'−∠Y'X'Z'
=360゜−2(60゜+β)−2(60゜+α)−60゜
=60゜−2(α+β)
=60゜−2(60゜−γ)
=2γ−60゜
またX'P=X'Y'=X'Z'=X'Qであるから
∠X'PQ
=∠X'QP
=(180゜−∠PX'Q)÷2
={180゜−(2γ−60゜)}÷2
=120゜−γ
∠X'PA'=∠X'Y'A'=60゜+γ
∴∠X'PQ+∠X'PA'=180゜
∠X'QB'=∠X'Z'B'=60゜+γ
∴∠X'QP+∠X'QB'=180゜
よって4点A',P,Q,B'は一直線上にある。
したがって、
∠B'A'X'=∠PA'X'=∠Y'A'X'=α
∠A'B'X'=∠Q'B'X'=∠Z'B'X'=β
同様に、
∠C'A'Y'=∠X'A'Y'=α
∠C'B'Z'=∠X'B'Z'=β
∠A'C'Y'=∠Z'C'Y'=γ
∠B'C'Z'=∠Y'C'Z'=γ
がいえる。これらから対応する2角が等しいから
△ABX∽△A'B'X'、
△ABC∽△A'B'C'
△ACY∽△A'C'Y'
∴AX:A'X'=AB:A'B'=AC:A'C'=AY:A'Y'
また∠XAY=∠X'A'Y'
∴△AXY∽△A'X'Y'
同様に
△BCZ∽△B'C'Z'、
△BXZ∽△B'X'Z'
△CYZ∽△C'Y'Z'
これらから
∠BXZ=∠B'X'Z'、
∠AXB=∠A'X'B'、
∠AXY=∠A'X'Y'であるから
∠ZXY=∠Z'X'Y=60゜
同様に∠XYZ=60゜がいえるから、△XYZは正三角形である。
◆宮城県 アンパンマン さんからの解答。
∠BAX=∠XAY=∠YAC=α
∠ABX=∠XBZ=∠ZBC=β
∠BCZ=∠ZCY=∠YCA=γとする。
α+β+γ=60゜
△ABCの外接円の直径をDとする。
BX
=ABsin(α)/sin(π-α-β)
=Dsin(3γ)sin(α)/sin(α+β)
=Dsin(3γ)sin(α)/sin(π/3-γ)
同様に
BZ=Dsin(3α)sin(γ)/sin(π/3-α)
sin(3λ)=4sin(λ)sin(π/3-λ)sin(π/3+λ) より
BX=4Dsin(γ)sin(α)sin(π/3+γ)
BZ=4Dsin(α)sin(γ)sin(π/3+α)
XZ2 =BX2+BZ2-2BX.BZcos(β) =[4Dsin(α)sin(γ)]2.[sin(π/3+γ)2+sin(π/3+α)2-2sin(π/3+γ)sin(π/3+α)cos(β)]
4sin(A)sin(B)cos(C) =-cos(A+B+C)-cos(A+B-C)+cos(B+C-A)+cos(A+C-B)より
XZ2
={[4Dsin(α)sin(γ)]2}/2.[1-cos(2π/3+2γ)+1-cos(2π/3+2α)-{-cos(π)-cos(π-2β)+cos(π/3-2γ)+cos(π/3-2α)}]
={[4Dsin(α)sin(γ)]2}/2.(1-cos(2β))
=[4Dsin(α)sin(γ)]2.sin(β)2
XZ=4Dsin(α)sin(γ)sin(β)
同様に
XY=YZ=4Dsin(α)sin(γ)sin(β)
よって△XYZは正三角形である。