3
◆愛知県 Y.M.Ojisan さんからの解答。
【解答】
円の面積はπr2です(中学1年)。
そこで、r=1の円の面積で評価を行います。
もう一つ、3平方の定理(中学3年)を下記恒等式として用います。
x2+y2=1
| ここで x= | 1−t2 1+t2 |
、y= | 2t 1+t2 |
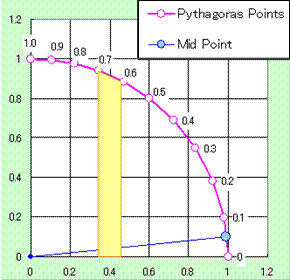
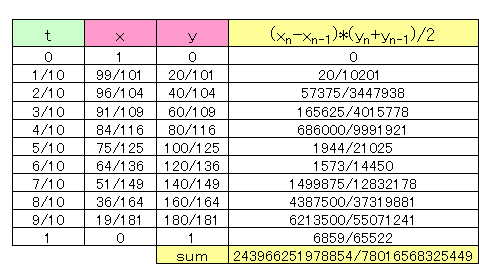
| それは | π 4 |
より小さい値です。上図参照。 |
| これを計算し、4倍すると | 243966251978854 78016568325449 |
であり、 |
| 座標は ( | 100 101 |
, | 10 101 |
)です。 |
| r2=( | 100 101 |
)2+( | 10 101 |
)2= | 100 101 |
である円の面積は、 |
| 即ち π* | 100 101 |
< | 243966251978854 78016568325449 |
です。 |
| つまり π< | 121983125989427 38622063527450 |
です。 |
手間を別にして、問題2も中学レベルで解く方法を考えてみました。
円の面積=πr2の根拠を子供に質問されたときに、結局例の、扇形を櫛状に並べ組み合わせて、極限の思想で説明する以外無いように思います。
これは積分ですから本来高校レベルですね。
だから、やめろとか言うつもりは毛頭ないのですが、円の面積=πr2が中学で教えられることの純数学的意味を考えさせられる解答となりました。
この辺の曖昧さに関して、http://www004.upp.so-net.ne.jp/s_honma/circle/circle4.htmに良くまとめられていると思います。
◆東京都 甘泉法師 さんからの解答。
【問題1】
『平均と数列』の問題3の数列は、扇形の円弧の長さを、それぞれ、内側から、外側から評価する式になっており、
| 極限値は | 4π 3 |
。 |
【問題2】
同じく、第8項を計算して、 π<3.1597 .
中心角120度の弧の8分割(すなわち外接正24角形)の周の長さを評価しています。
◆高知県 blue さんからの解答。
【問題1】
半径1の円Aに内接する正12角形Bを考える。
Aの円周>Bの周りの長さ、である。
ここで、頂角30°、二辺の長さが1の二等辺三角形の残りの辺の長さは
三平方の定理を使った計算から√(2−√3)である。
したがって、2π>12√(2−√3)
π>6√(2−√3)
| =6√( | 4−2√3 2 |
) |
√2>1.414 より 3√2>4.242 (>0)
√3>1.732 より √3−1>0.732 (>0)
辺々を掛け合わせて
3√2(√3−1)>3.105144
∴π>3√2(√3−1)>3.105144>3.1
【問題2】
半径1の円Aに外接する正24角形Cを考える。
Aの面積<Cの面積、である。
ここで、頂角15°、頂角から対辺におろした垂線の長さが1である二等辺三角形の
| 等しい二辺の長さは | 1 cos(15°/2) | である。 |
| したがって、π<24( | 1 2 | (sin(15°)) | ( | 1 cos(15°/2) | ) | 2 |
| ( | 1 cos(15°/2) | ) | 2 | = | 2 1+cos(15°) |
| π< | 24sin(15°) 1+cos(15°) | --------(1) |
| (sin(15°))2=(sin(30°/2))2= | 1-cos(30°) 2 | = | 2-√3 4 |
| 故に、sin(15°)= | √(2-√3) 2 |
| (cos(15°))2=(cos(30°/2))2= | 1+cos(30°) 2 | = | 2+√3 4 |
| 故に、cos(15°)= | √(2+√3) 2 |
| π< | 24(√3−1) 2√2+√3+1 |
| したがって、 | 1 2√2+√3+1 |
< | 1 5.560 |
---------(2) |
| 24(√3−1) 2√2+√3+1 |
| < | 17.56944 5.560 |
| ∴ π< | 24(√3−1) 2√2+√3+1 |
<3.1599712230215827338129496402878<3.16 |