『拡張ペル方程式』解答

◆東京都　BossF さんからの解答。

【問題１】

背理法を用いる

a=n3(n∈N)と仮定し、ny=q , n2z=rとおけば

与式の左辺
=x3+q3+r3-3xqr
=(x+q+r)(x2+q2+r2-xq-qr-rx)
=1

ここで、
x2+q2+r2-xq-qr-rx= (x-q)2+(q-r)2+(r-x)2
2		≧0だから

x+q+r=1が必要、
ところが、{x,q,r}⊂Nだから矛盾

◆愛知県　Y.M.Ojisan さんからの解答。

【問題】

自然数ｘ，ｙ，ｚ，ａが以下の等式を満たしている。
ｘ3＋ａｙ3＋ａ2ｚ3−3ａｘｙｚ＝1 −（１）

【問題１，２解答】

方程式（１）に対応して　成分　t0,t1,t2が下記である３次元空間内の非等方格子点の集合をＴとする。

Ｔ ∋ (t0,t1,t2) ＝（ｘ,a1/3ｙ,a2/3ｚ）　　　

また　Ｔから実数空間Ｒへの写像Ｆを下記のように定義する。
さらに　集合F（Ｔ）をＬとする。

　F（ｔ）＝t0+t1+t2 ∈Ｌ⊂Ｒ　ｔ∈Ｔ

ここで、aが立方数でないとき、即ちa1/3が無理数であるとき、写像　F　は１対１写像である。
証明省略。

　さらにＲでの乗算および1, a1/3, a2/3の倍数を意識して、
Ｔでの演算 ・ を下記のように定義する。
なお、×,+は通常の算法。

ｓ，ｔ∈Ｔ

ｓ・ｔ＝（s0×t0+s1×t2+s2×t1 , s0×t1+s1×t0+s2×t2 , s0×t2+s1×t1+s2×t0）∈Ｔ
すなわち、 Ｔは演算 ・　により群になっている。

次に、ノルムを意識した下記評価関数を定義する。

ｔ∈Ｔ

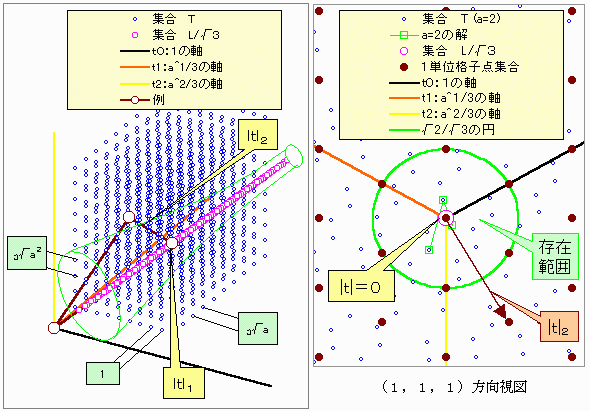
｜ｔ｜＝０．５×｜ｔ｜1×｜ｔ｜2
｜ｔ｜1：ｔの(1,1,1)方向の成分×＝t0+t1+t2 ＝Ｆ（ｔ）∈Ｌ
｜ｔ｜2：ｔの(1,1,1)方向軸線との距離の２乗×３　＝(t1-t2)2+(t2-t0)2+(t0-t1)2
一方　｜ｔ｜を（ｘ、a1/3ｙ、a2/3ｚ）で表すと、下記であり（１）の左辺である。

｜ｔ｜
＝（t03 +t13+t23 -3*(t0*t1*t2)）
＝（x3 +aｙ3+a2z3 -3axyz）

また、ｓ，ｔ∈Ｔ　に対して
｜ｓ｜×｜ｔ｜＝｜ｓ・ｔ｜であり、・ に対応するノルム？である。

∵　定義より
｜ｓ｜1×｜ｔ｜1＝｜ｓ・ｔ｜1　は明らかである。

　また、

｜ｓ｜2×｜ｔ｜2
＝｛(t1-t2)2+(t2-t0)2+(t0-t1)2}×{(s1-s2)2+(s2-s0)2+(s0-s1)2}
＝４×{(t1-t0)2+(t2-t0)2+(t1-t0)(t2-t0)}×{(s1-s0)2+(s2-s0)2+(s1-s0)(s2-s0)}
一方
 ｜ｓ・ｔ｜2
＝{s0(t1-t2)+s1(t0-t1)+s2(t2-t0)}2+{s0(t2-t0)+s1(t1-t2)+s2(t0-t1)}2……
＝{s0(t1-t0-t2+t0)+s1(t0-t1)+s2(t2-t0)}2+{s0(t2-t0)+s1(t1-t0-t2+t0)-s2(t1-t0)}2……
＝{-(s1-s0)(t1-t0)+(s2-s0)(t2-t0)}2+{(s1-s0-s2+s1)(t1-t0)-(s1-s0)(t2-t0)}2……
＝２×{(t1-t0)2+…..省略
を計算すれば　

{0.5×｜ｓ｜2}×{0.5×｜ｔ｜2}＝０.5×｜ｓ・ｔ｜2 が成立していることがわかる。

○問題１

（１）を満たす　t∈Ｔ　に対して

｜ｔ｜2＝２｜ｔ｜／｜ｔ｜1＝２／Ｆ（ｔ）である。

ｘ ｙ ｚ aは自然数なので　Ｆ（ｔ）≧３であるから、
少なくとも｜ｔ｜2≦２／３である。

等号はt0=t1=t2=1 の場合のみ成立するが

このとき｜ｔ｜2＝０である。

よって、｜ｔ｜2＜２／３　for ｜ｔ｜＝１。

　一方、　Ｔを含む３次元空間の単位１の格子点間の、べクトル（１，１，１）に直交する面内での、
最少距離の平方は２／３である。

ａが立方数である場合　Ｔは単位１の格子点集合に含まれる。

従って　t0=t1=t2＝整数の点を含むが、
この点では｜ｔ｜2＝０　であり（１）は成立しない。

　隣の格子点までの距離の平方は２／３以上であるので、
｜ｔ｜2＜２／３であるものは存在しない。

よって、ａが立方数である場合に（１）を満足するものはない。

○問題２

（１）即ち　｜ｔ｜＝１　ｔ∈Ｔ　が存在するとき　
ｔm∈Ｔ　は｜ｔm｜＝１　　であり（１）を満足する。

ここでｔmはｍ個のｔの・積　t・ｔ・ｔ・ｔ。。。である。

F(t)＝t0+t1+t2＞３　であるから、
ｔmの値は無限に存在する。
問題１よりａは立方数ではない。

従って　ｔmの値と１対１対応の
（(tm)0,(tm)1,(tm)2）の組＝(x,y,z)の組は無限に存在する。

【感想】

　とても深く美しい問題ですね｡

ペルの方程式がこのように拡張できるとは思いもよりませんでした｡
元の２元数としてのノルムと拡張後の３元数としてのノルムの関連性がまだ見えていません。

ノルムといえばスカラー積（２次）が普通なので、３次のノルムというのも私には新鮮でした｡
４元数への拡張も出来るのでしょうか。
ノルムが１次ノルムと２次ノルムの合成になっているのには何か数学的意味が有るのでしょうか。
興味は尽きません｡

　『拡張ペル方程式』へ

　数学の部屋へもどる