◆愛知県 Y.M.Ojisan さんからの解答。
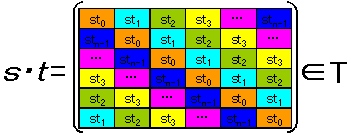
問題の行列をtとする。
添え字の加減演算はMODnで行うものとし、
添え字範囲を0〜n−1にずらすと、下式で表記できる。
以後も同じ表現とする。
![]()
【補題1】
行列tの性質をもつ行列の集合をTで表すとき,T の任意の2要素の積はTの要素である。


なぜなら、以下であるからである。
ここでY,Zは自然数である。
記号法として、縮約を用いた。
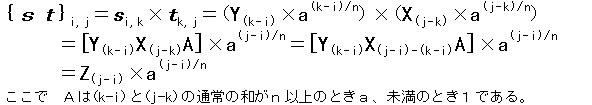

【補題2】
行列式の性質より、以下が成立する。
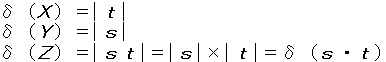
【補題3】
Tの要素に対して 下記で定義される | |1はノルムの特性をもつ。
![]()
なぜなら、以下であるからである。
![]()
【問題1】
下記 Uを定義する.
|U|=1であるから
|t|=1 に対し |tU|=1である。
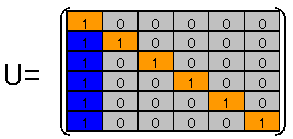
tUの計算を行うと、 Q=n|t|1
とおくことにより、下記のように計算される。
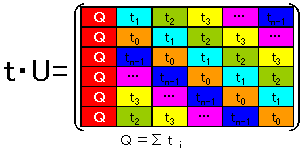
この式の行列式を計算し、行列式からQを抜き出し整理すると、以下である。

Qはn以上であり、従って、上記の右辺の行列式は1未満の正の数である。
一方、aがn乗数であると、右辺行列の各要素は整数であり,その行列式も整数である。
しかし、正の整数で1以下のものはない。
よって、aはn乗数ではない。
【問題2】
|t|=1であるとき、補題1および補題2により
|tm|=1 m:任意自然数であり、
tm は条件を満足する行列である。
また、|t|1=1となるのは
各Xiおよびaが1のときのみであり,
この時|t|=0であるから矛盾する。
従って|t|1>1である。
![]()
補題3により、
|tm|1=|t|1m である。
|t|1>1であるから、m が異なれば
|tm|1は異なる。
よって、|tm|=1を満足するtmは自然数の程度で無限にある。
【P.S.】
問題1は 行列式が 各列ベクトルを1辺とする「n次元の平行四辺形」の体積であることを使えば、
列ベクトルのuに直交する成分の長さ
(全部同じ長さなのでどの列でもよい)
が、単位1の格子点では 最小でも(1−1/n)0.5 であって、
(定数/Q)1/(n-1)の最大値との関係から成立しないというpart1と同じ幾何学的な方法もある。