◆静岡県 ヨッシー さんからの解答。
平行四辺形の対称性から、直線XYが平行四辺形ABCDの対角線の中点Oを通ることを示せばよい。
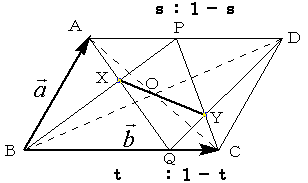
| → BA | = | → a | 、 | → BC | = | → b | とおき、 |
AP:PD=s:1−s
BQ:QC=t:1−t とする。
ただし0<s<1、0<t<1。
このとき、
| → BX | = | t s+t | → BP | = |
t s+t |
→ a | + | st s+t | → b |
| → BY | = | → BQ | + | 1-t 2-s-t | → QD | = |
1-t 2-s-t |
→ a | + | 1-st 2-s-t | → b |
となり、これに対して、
| → BZ | = | s+t 2 | → BX | + | 2-s-t 2 |
→ BY |
を計算すると、
| → BZ | = | → BX | /2+ | → BY | /2= | → BO |
となり、点Oは、直線XY上にあり、直線XYは、平行四辺形ABCDの面積を2等分する。

◆鹿児島県 ともひろ さんからの解答。
【ベクトルOXおよび、ベクトルOYの関係について】
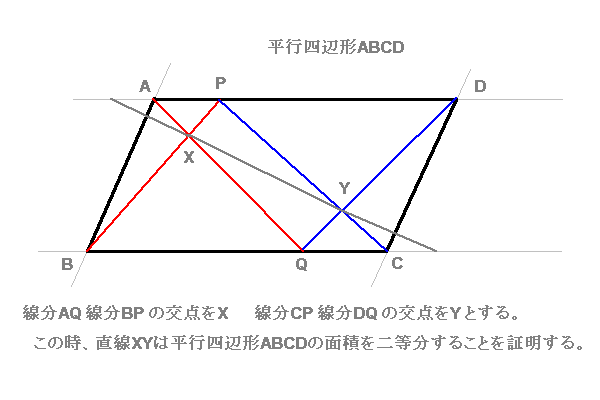
平行四辺形ABCDにおいて、線分AD上の点P、線分BC上の点Qをおく。
(AD=BC=1 として、AP=m CQ=nとする)
線分AQ 線分BPの交点を点X 、線分CP 線分DQの交点を点Yとする。
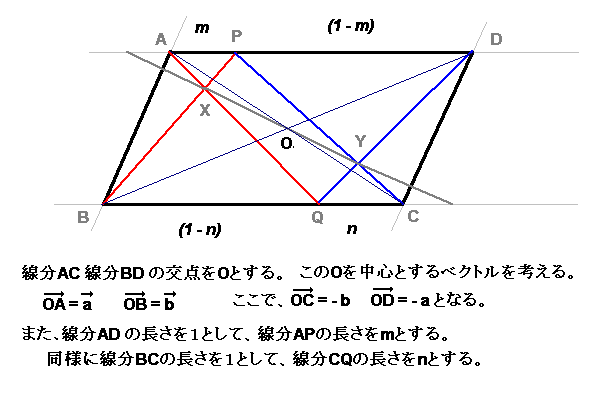
ここで、対角線として線分ACと線分BDの交点を点Oとして、これを原点とするベクトルを考える。
| → OA | = | → a | , | → OB | = | → b | とする。 |
また、
| → OC | =- | → OA | =- | → a | , |
| → OD | =- | → OB | =- | → b | とする。 |
| → OX | = | → OA | + | → AX | とする。 |
△AXPと△QBXにおいて、
∠AXPと∠QXBは対称角だから、
∠AXP = ∠QXB
∠APXと∠QBXは鎖角だから、
∠APX = ∠QBX
二角が等しいので、
△AXP ∽ △QXB
また、
AP:QB
=mAD:(1-n)BC
=mAD:(1-n)AD
=m:1−nなので、
AX:QX=m:1−n
よって、
| → AX | = | m m+(1-n) | → AQ | = | m 1+m+n |
→ AQ |
| → AQ | = | → BQ | - | → BA |
| → BQ | =(1-n) | → BC | = (1-n) | → AD |
| → AD | = | → OD | - | → OA |
= - | → b | - | → a |
= -( | → a | + | → b | ) |
| → BA | = | → OA | - | → OB | = | → a | - | → b |
| → AQ | = (n-1)( | → a | + | → b | ) - ( | → a | - | → b | ) |
= (n-2) | → a | +n | → b |
| → OX | = | → a | + | m 1+m+n | ( (n - 2) |
→ a | +n |
→ b | ) |
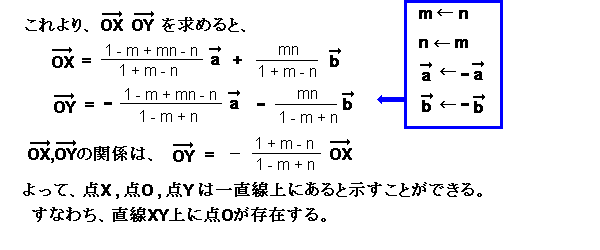
| → OX | = | 1-m+mn-n 1+m-n |
→ a | + | mn 1+m-n |
→ b |
ここで、 | → OY | については | → OX | の式に |
n ← m
| → a | ← - | → a |
| → b | ← - | → b |
と置き換えて整理すると、
| → OY | =- | 1-m+mn-n 1-m+n |
→ a | - | mn 1-m+n |
→ b |
| → OY | =- | 1+m-n 1-m+n |
→ OX |
となり、
| → OY | = | k |
→ OX | と表すことができる。 |
したがって、点X、点O、点Yは同一直線上に存在することから、
点0は直線XY上に存在する。‥‥(1)
【平行四辺形ABCD内の点Oを通る直線について】
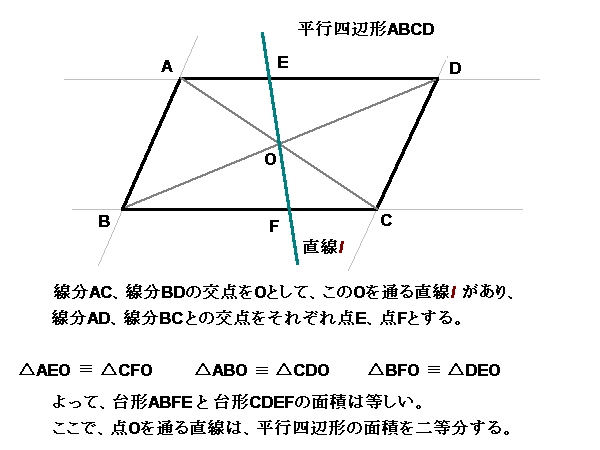
平行四辺形ABCDにおいて、対角線、線分ACと線分BDの交点を点Oとする。
また、この点Oを通る直線lがあり、線分ADと線分BCとの交点をそれぞれ、点E、点Fとする。
ここで、点Oは線分ACと線分BDの中点であり(証明略)また、
△AEO ≡ △CFO より、面積は等しい。
△ABO ≡ △CDO より、面積は等しい。
△BFO ≡ △DEO より、面積は等しい。
ゆえに、台形ABFE と 台形CDEFの面積は等しい。
したがって、点Oを通る直線は、平行四辺形ABCDの面積を二等分する。‥‥(2)

【結論】
点X、点O、点Yは同一直線上に存在することから、
点0は直線XY上に存在する。‥‥(1)
点Oを通る直線は、平行四辺形ABCDの面積を二等分する。‥‥(2)
このことから、直線XYは(点Oを通ることから)平行四辺形ABCDの面積を二等分する。
(証明終わり)
◆宮城県 アンパンマン さんからの解答。
XYはADの平行線ではない場合を考えます。
XYとADの交差点をM。XYとBCの交差点をN。
XYとABの交差点をR。XYとCDの交差点をS。
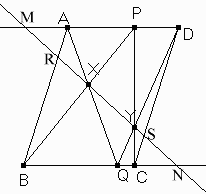
メネラウスの定理から
| BN NC |
* | CY YP |
* | PX XB |
=-1 |
| AX XQ |
* | QY YD |
* | DM MA |
=-1 |
| AX XQ |
= | PX XB |
と | QY YD |
= | CY YP |
から |
| DM MA |
= | BN NC |
が成り立つ。 |
四角形ABCDは平行四辺形から
四角形BRSC=四角形DSRA。
AMの長さが無限大に収束するとXYとADは平行になります。
従ってXYは平行四辺形ABCDの2等分線です。
◆青木注
メネラウスの定理
三角形 ABC と それに交わる直線 L が与えられたとする。
L と AB との交点を X, L と BC との交点を Y, L と CA との交点を Z とすると、次の等式が成り立つ。
![]()
◆神奈川県の中学校2年生 わたなべ さんからの解答。
パップスの定理よりX,Y,この平行四辺形の対角線の交点は一直線上にある。
よって直線XYは平行四辺形の対角線の交点を通るので、この平行四辺形の面積は二等分される。
◆青木注
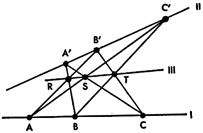
パップスの定理。
A,B,Cは直線Iの上の任意の3つの点。
A',B',C'は直線IIの上の任意の3つの点。
このときこれらの点を以下のように結んだ直線の交点R,S,Tは一直線上(直線III)に並ぶ。