◆愛知県 Y.M.Ojisan さんからの解答。
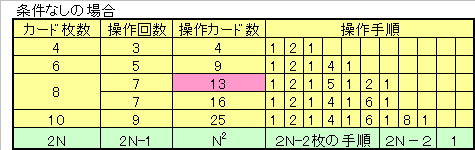
【条件なし】
下表に解答を示す。
一般解として下表最下段に示すものがあるが、最小かどうかは不明(未証明)。
カードが8枚のとき、この一般解の系列外の解がある。

【上半分条件付】
下表に解答を示す。
最小の一般解を最下段に示す。
∵ 初期に下半分が全部同じ場合を考える。
2N−1未満の手順数では、上半分のNbitのパターンで網羅されないものがでる。
初期状態を操作してこの網羅されない場合を下半分と逆転する場合にすることが可能であり、同数にできない場合となる。
よって、背理法により最小操作回数は2N−1以上である。
つまり、Nbitのパターン全部を巡る必要がある。
そのような方法は幾つかあるが、操作カード枚数を最小にするには、束の中心のカードほど反転させる回数を少なくする方が良く、下表の方法が最小である。

◆出題者のコメント。
解答ありがとうございます。
【操作するカードが上半分に限らない場合】
操作回数,操作枚数とも正解です!
8枚(N=4)の時の例外的な解の発見も流石です。
少しでも考え方を示して頂ければ有り難かったですが・・・。
【操作するカードが上半分に限る場合】
操作回数,操作枚数とも正解です!
操作枚数を最少にするための考察もお見事です。
カードの上から順に20,21,22,…,2N-1と対応させ、
初期と同じを「0」初期の反対を「1」で表すと、
上半分のカードで起きうるすべての状態は、
2N個の2進数で表せることになります。
これは10進数の0〜(2Nー1)に対応しています。
8枚(N=4) の時の上半分を例に示します。
| 10進数 | 2進数 | 右から何番目に 最初の1があるか? |
| 0 | 0000 | 初期状態 |
| 1 | 0001 | 1 |
| 2 | 0010 | 2 |
| 3 | 0011 | 1 |
| 4 | 0100 | 3 |
| 5 | 0101 | 1 |
| 6 | 0110 | 2 |
| 7 | 0111 | 1 |
| 8 | 1000 | 4 |
| 9 | 1001 | 1 |
| 10 | 1010 | 2 |
| 11 | 1011 | 1 |
| 12 | 1100 | 3 |
| 13 | 1101 | 1 |
| 14 | 1110 | 2 |
| 15 | 1111 | 1 |
上のどの行の状態も一回の操作ですぐ下の行の状態になります。
ですから操作回数はすべての状態から初期を除いた2Nー1です。
操作手順は「右から何番目に最初の1があるか?」の数と同じ枚数を、上から下に順に裏返し操作をすれば、Y.M.Ojisan さんも示されたような 対称性のある最少枚数の解が得られます。