
仧峀搰導丂惔愳丂堢抝偝傫偐傜偺夝摎丅
丂僇僞儔儞悢偵側傞偙偲偑梊憐偝傟傑偡丅
嵟弶偼俆侽侽墌峝壿傪帩偭偨惗搆偐傜廤嬥偟傑偡丅
値亖侾仺侾
値亖俀仺俀
値亖俁仺俆
値亖係仺侾係
| 2n俠n 乗乗乗乗 値亄侾 | 亖 | 俀値両 乗乗乗乗乗乗乗乗 値両亊乮値亄侾乯両 |
乽嶰妏宍偵暘偗傞偲乿偲摨偠栤戣偵側傞偺偑晄巚媍偱偡丅
徹柧偑傑偩弌棃傑偣傫丅
嶼僠儍儗儊乕儕儞僌儕僗僩偱傕僇僞儔儞悢偑榖戣偵側偭偰偄傑偡丅
亂僐儊儞僩亃
丂偆乕傓丄偡傞偳偄丅
徹柧偼彂偙偆偲巚偆偲寢峔戝曄偱偡偑丄偤傂偍婅偄偟傑偡丅
巹傕乽嶰妏宍偵暘偗傞偲乿偲摨偠偲偄偆偺偼晄巚媍偱偡丅
仧峀搰導丂惔愳丂堢抝偝傫偐傜偺夝摎丅
丂俆侽侽墌嬍傪帩偭偰偄傞惗搆値恖丄侾侽侽侽嶥傪帩偭偰偄傞惗搆値恖傪侾楍偵暲傋傞丅
偦偺応崌偺悢偼丄2n俠n 捠傝偱偡丅
壗斣栚偱傕偄偄偑丄壖偵倣斣栚偺愮墌嶥傪帩偭偰偄傞惗搆偱偮傝慘偑弌偣側偄応崌傪峫偊傞丅
偮傝慘偑弌偣側偄応崌偺悢偼丄2n俠n-1捠傝偱偡丅
偟偨偑偭偰丄偮傝慘偑偄傜側偄偱丄俀値恖偺惗搆偐傜廤嬥偑弌棃傞応崌偺悢偼丄
丂2n俠n亅2n俠n-1
| 亖 | 2n俠n 乗乗乗乗 値亄侾 |
| 亖 | 俀値両 乗乗乗乗乗乗乗乗 値両亊乮値亄侾乯両 |
僇僞儔儞悢傪峫偊傞偲偒丄杮幙揑偱偐偮僔儞僾儖偱旕忢偵椙偄栤戣偩偲巚偄傑偡丅丂
亂僐儊儞僩亃
丂偙傟偼暘偐傝傗偡偄寁嶼偱偡偹丅
乽嶰妏宍偵暘偗傞偲乿偺夝摎偺拞偺夞婣揑側岞幃傪巊偭偰帵偟偰傕丄柺敀偄偺偱偼側偄偱偟傚偆偐丅
仧峀搰導丂惔愳丂堢抝偝傫偐傜偺夝摎丅
| 俀値両 乗乗乗乗乗乗乗乗乗 値両亊乮値亄侾乯両 |
悢妛揑婣擺朄偵傛傝徹柧偡傞丅
値亖侾丂偺偲偒丂俆侽侽丆侾侽侽侽丂偺侾捠傝丅 丂
| 俀両 乗乗乗乗乗乗乗乗乗 侾両亊乮侾亄侾乯両 | 亖侾 |
値亖倠丂偺偲偒
| 冊亖 | 俀倠両 乗乗乗乗乗乗乗乗乗 倠両亊乮倠亄侾乯両 |
値亖倠亄侾丂偺偲偒
乮俀倠亄俀乯斣栚丄懄偪嵟屻偺惗搆偼侾侽侽侽墌嶥傪帩偭偨惗搆偵側傞丅
俆侽侽墌嬍傪帩偭偨惗搆偺楍偵擖傞偙偲偺偱偒傞応強偼丄乮俀倠亄侾乯売強丅
偙偺楍偼偮傝慘側偟偵廤嬥偱偒傞丅
傑偨偙偺楍偺俀倠斣栚偺惗搆偲乮俀倠亄侾乯斣栚偺惗搆傪擖傟懼偊偨楍傕丄偮傝慘側偟偵廤嬥偱偒傞丅
偙偺偙偲偼偳偺楍偵懳偟偰傕尵偊傞丅
乮冊亊乮俀倠亄侾乯亊俀乯偼丄幚嵺偵壜擻側楍偺倄攞偵側偭偰偄傞丅
倄亖(k+1)+1俠1亖k+2俠1亖倠亄俀丅
偟偨偑偭偰媮傔傞楍偺応崌偺悢偼丄
丂
| 俀倠両 乗乗乗乗乗乗乗乗乗 倠両亊(倠亄侾)両 | 亊 | (俀倠亄侾)亊俀 乗乗乗乗乗乗乗乗乗 倠亄俀 |
| 亖 | 俀倠両亊(係倠亄俀) 乗乗乗乗乗乗乗乗乗 倠両亊(倠亄俀)両 |
暘巕丄暘曣偵乮倠亄侾乯傪妡偗傞丅
| 亖 | (倠亄侾)亊(係倠亄俀)亊俀倠両 乗乗乗乗乗乗乗乗乗乗乗乗乗乗 (倠亄侾)亊倠両亊(倠亄俀)両 |
| 亖 | (俀倠亄俀)亊(俀倠亄侾)亊俀倠両 乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗 (倠亄侾)両亊(倠亄俀)両 |
| 亖 | (俀(倠亄侾))両 乗乗乗乗乗乗乗乗乗乗乗乗乗乗乗 (倠亄侾)両亊((倠亄侾)亄侾))両 |
忋幃偼丂値亖倠亄侾丂偺偲偒傕惉傝棫偮偙偲傪昞傢偟偰偄傞丅
埲忋偱偡丅
僇僞儔儞悢偺慟壔幃偺堦偮偲偟偰丄
| 俙n+1亖 | 係値亄俀 乗乗乗乗乗乗 値亄俀 |
亊俙n |
仧愇愳導丂悢妛岲偒丂偝傫偐傜偺夝摎丅
丂夝摎偱偼側偄偺偱偡偑丄傛偆傗偔栤戣偺堄枴偑暘偐傝傑偟偨丅
屲昐墌嬍傪仠丄愮墌嶥傪仜偱昞偡偲丄
丒値亖侾偺帪丄
丒値亖俁偺帪丄
仧弌戣幰偺丂悈偺棳傟丂偝傫偺夝摎丅
栤戣偺拞偱丄500墌嬍傪暐偆偺傪俙丆1000墌嬍傪暐偆偺傪俛偲偟傑偡丅
掁傝慘偑側偄偺偱丄忢偵俙偺悢偑俛偺悢傛傝摍偟偄偐戝偒偗傟偽傛偄偺偱偡丅
値亖侾偺偲偒丄俙俛 偺侾捠傝
値亖俀偺偲偒丄俙俙俛俛丆俙俛俙俛 偺俀捠傝
値亖俁偺偲偒丄
丂俙俙俙俛俛俛丆
丂俙俙俛俙俛俛丆
丂俙俙俛俛俙俛丆
丂俙俛俙俙俛俛丆
丂俙俛俙俛俙俛 偺俆捠傝
偙偙偱丄峫偊曽傪曄偊偰丄偙傟傪俙傪仺丄俛傪仾偲昞偣偽丄
仺偑値屄丄仾 偑値屄偺摨偠傕偺傪堦楍偵暲傋傞曽朄偲峫偊傜傟傑偡丅
偩偐傜丄岄斦偺栚傪偟偨嵟抁宱楬偺栤戣偵曄壔偟偰偄偒傑偡丅
暘偐傝堈偔偡傞偨傔偵丄媮傔傞悢傪俲(n)偲偡傞偲丄
俲(侾)亖侾丆俲(俀)亖俀丆俲(俁)亖俆
偼恾傪彂偄偰丄暘偐傞偲偟傑偡丅
偙偺俲(n)偺悢楍傪僇僞儔儞悢偲尵偄傑偡丅
値亖係偺偲偒傪昤偒傑偡丅
恾偺傛偆側仮俙俛俠偺嵟抁宱楬偺摴嬝偑俲(係)偵側傝傑偡丅

亙峫偊曽偐傜偺暃嶻暔亜
俲(係)傪媮傔傞偺偵丄
(鶣)俛侾傪捠傞偲偒丄俙偐傜 俛侾傪捠傝丄仮俛侾俢俛偺嵟抁宱楬俲(俁)偺摴嬝
(鶤)俛侾傪捠傜偢丄俛2傪捠傞偲偒丄
仮GHL偺嵟抁宱楬俲(侾)偐傜丄摴楬俴俛俀傪捠傝丄仮俛俀俤俛偺嵟抁宱楬俲(俀)偺摴嬝
(鶥)俛侾丄俛俀傪捠傜偢丄俛俁傪捠傞偲偒丄
仮俧俬俵偺嵟抁宱楬俲(俀)偐傜丄摴楬俵俛俁傪捠傝丄仮俛俁俥俛偺嵟抁宱楬俲(侾)偺摴嬝
(鶦) 嵟屻偵丄俛侾丆俛俀丄俛俁傪捠傜偢丄俛偵峴偔応崌偼
仮俧俠俥偺嵟抁宱楬俲(俁) 偵摍偟偄丅
傛偭偰丄
丂俲(係)
亖 俲(俁)亄俲(侾)俲(俀)亄俲(俀)俲(侾)亄 俲(俁)
亖俆亄侾亊俀亄俀亊侾亄俆亖侾係 偵側傝傑偡丅
偙傟偼丄堦斒偵 俲(侽)亖侾偲寛傔偰偍偗偽丄
K(値)亖K(0)K(n亅1)亄K(1)K(n亅2)亄K(2)K(n亅3) 亄丒丒丒亄K(n亅1)K(0)偲偄偆丄慟壔幃偑惉傝棫偪傑偡丅
傑偨丄偙傫側悢偊曽(彂偒崬傒曽幃)傕偱偒傑偡丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂14俛 丂丂丂丂丂丂丂丂丂丂丂丂丂丂仾 丂丂丂丂丂丂丂丂丂丂丂丂俆仺14俥 丂丂丂丂丂丂丂丂丂丂丂丂仾丂仾 丂丂丂丂丂丂丂丂丂丂俀仺俆仺俋俤 丂丂丂丂丂丂丂丂丂丂仾丂仾丂仾 丂丂丂丂丂丂丂丂侾仺俀仺俁仺係俢 丂丂丂丂丂丂丂丂仾丂仾丂仾丂仾 丂丂丂丂丂丂俙仺侾仺侾仺侾仺侾俠偝傜偵丄幬傔偺慄偵娭偟偰偺懳徧惈偵婥偑偮偗偽丄
K(係)亖 侾亊侾亄俁亊俁亄俀亊俀亖侾係偟偨偑偭偰丄僇僞儔儞悢俲(値)偼壗屄偐偺暯曽悢偺榓偱偱偒偰偄傑偡丅
K(俆)亖 侾亊侾亄係亊係亄俆亊俆亖係俀
K(俇)亖 侾亊侾亄俆亊俆亄俋亊俋亄俆亊俆亖侾俁俀
偝偰丄杮戣偵擖傝傑偡丅値亖係偱昤偒傑偡丅

仩俢俙俠俛偺嵟抁宱楬偺摴嬝偼丄奒忔偺婰崋傪巊偊偽丄
(係亄係)両亐(係両亊係両)亖俈侽 捠傝 偁傝傑偡丅
偙偙偐傜丄懳妏慄俙俛偲岎傢傞宱楬偑晄揔偱偡偐傜丄偙偺晄揔側宱楬傪媮傔傑偡丅
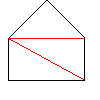
椺偊偽丄恾偺懢慄偺宱楬偼晄揔偱偡偑丄偙傟傪捈慄俿侾俿係偵偮偄偰懳徧堏摦偟傑偡丅
偨偩偟丄捈慄俿侾俿係偵巒傔偰弌夛偭偨揰偐傜屻偺晹暘偺傒傪懳徧偵嬋偘偰恾偺懢偄攇慄傪峫偊傞偲丄慡偰偺晄揔側宱楬偼仩俙俤俥俧偺嵟抁宱楬偺悢偵摍偟偔側傝傑偡丅
偙傟偼丄 (俆亄俁)両亐(俆両亊俁両)亖俆俇 捠傝偲側傝丄
媮傔傞僇僞儔儞悢俲(係)偼丄慻崌傢偣偺婰崋傪俠(値丆倰)偲偡傟偽丄
K(係) 亖俠(俉丆係) 亅俠(俉丆俁)亖俈侽亅俆俇亖侾係 偵側傝傑偡丅
堦斒偵丄
丂K(値)
亖俠(俀値丆値) 亅俠(俀値丆値亅侾)
亖俠(俀値丆値)亐(値亄侾)
偲側傝傑偡丅
偦偙偱丄傑偨丄栤戣偱偡丅
師偺戜宍俙俛俠俢偺嵟抁宱楬偼壗捠傝偁傝傑偡偐丅

尋媶 僇僞儔儞偺栤戣偺尨揟
偄偔偮偐偺悢偺愊偼丄俀偮偢偮偺悢偺愊偺寁嶼傪孞傝曉偟偰峴偭偰偄傞丅
偩偐傜丄偳偺俀偮偢偮偺愊傪嶌偭偰偄偔曽朄偺悢偼偳偆側傞偐偲偄偆栤戣(僇僞儔儞偺栤戣)偑丄侾俉俁俉擭偵僇僞儔儞偵傛偭偰榑偠傜傟偨丅
値屄偺悢偺弴彉偑曄傢傜側偄愊偺憤悢傪俠(値)偲偟丄
値屄偺悢偺弴彉傪曄偊偰傕椙偄愊偺憤悢傪俼(値)偲偡傞丅
嬶懱椺傪値亖侾丆俀丆俁丆係偱尒傑偡丅
(1) 値亖侾偺偲偒丄俠(侾)亖侾丄俼(侾)亖侾偲峫偊偰偍偔丅
(2) 値亖俀偺偲偒丄悢傪倎丆倐偲彂偔偲丄愊偼 倎倐丆倐倎 偺俀捠傝偱丄
俠(俀)亖侾丄俼(俀)亖俀 偲側傞丅
(3) 値亖俁偺偲偒丄悢傪倎丆倐丆們偲彂偔偲丄愊偼
(倎倐)們丆倎(倐們)丆(倎們)倐丆倎(們倐)丆
(倐倎)們丆倐(倎們)丆(倐們)倎丆倐(們倎)丆
(們倎)倐丆們(倎倐)丆(們倐)倎丆們(倐倎)
侾俀捠傝偱丄俠(俁)亖俀丄俼(俁)亖侾俀 偩偲傢偐傞丅
(4) 値亖係偺偲偒丄悢傪倎丆倐丆們丆倓偲彂偔偲丄悢偺弴彉偑倎丆倐丆們丆倓偲側傞愊偼
((倎倐)們)倓丆(倎倐)(們倓)丆(倎(倐們))倓丆
倎((倐們)倓)丆倎(倐(們倓))
偺俆捠傝側偺偱丄
俠(係)亖俆丄俼(係)亖俠(係)亊(係両)亖俆亊俀係亖侾俀侽丅
仏拲丗慜弎偺倠(値)偲俠(値)偺娭學偼
俠(値)亖俲(値亅侾) 偱偡丅
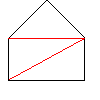
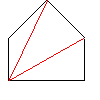
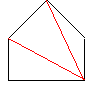
仏嶲峫丗値亞俀偺偲偒丄師偺惈幙偑偁傝傑偡丅
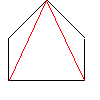
| 
| 
| 
| 
|
仏拲丗 E(n)亖C(n亅1)亖K(n亅2)偺娭學偲側傞丅
嶲峫丗1758擭偵僙僯僃乕儖偑敪尒偟偨慟壔幃
E(n)亖E(2)E(n亅1)亄E(3)E(n亅2)亄E(4)E(n亅3)丒丒丒亄E(n亅1)E(2)嵟屻偵丄僇僞儔儞悢楍傪彂偒傑偡丅
側偤丄擔忢惗妶偺偙傟傜偺尰徾偑侾偮偺悢楍偲偟偰丄尒側偝傟傞偐晄巚媍偱偡丅