◆石川県 数学好き さんからの解答。
N=2の時は1個。
N=3の時は5個。
N=4の時は15個。
(9+3+1+2)
N=5の時は35個。
(16+7+3+1+6+2)
以下は予想。
N=6の時は65個。
N=7の時は105個。
以上の結果をまとめると
N=2の時は1個。
N≧3の時は、5(N2−5N+7)個と予想できる。
【コメント】
さて、この予想は正しいでしょうか。
全国からのご意見をお待ちしています。
◆広島県 清川 育男 さんからの解答。
三角形の個数をSとする。
| S= | 1 ―― 3 | × | (2n−3)×(n2−3n+5) |
n=2のとき S=1。
n=3のとき S=5。
n=4のとき S=15。
n=5のとき S=35。
n=6のとき S=69。
n=7のとき S=121。
証明はできませんがこのように推理されます。
【コメント】
さて、また違った解答が来ました。
興味のある方、ぜひ確認してみてください。
◆東京都 goya さんからの解答。
(1つの頂点の石と隣接する石との長さをαで表わすと)
元の正三角形に含まれる上向きの正三角形の数は
・1辺の長さがαの正三角形の数は
最上段には1個、2段目には2個、・・・(N−1)段目(最下段)には(N−1)個ありますから
合計 N(N−1)÷2個
・同様に1辺の長さが2αの正三角形の数は
合計 (N−1)(N−2)÷2個
・1辺の長さがmαの正三角形の数は
合計 (N+1−m)(N−m)÷2個
また、それぞれの(m>2の)正三角形には図の様に辺上の同じ条件の位置にある石を結ぶことで(m−1)個の正三角形ができます。

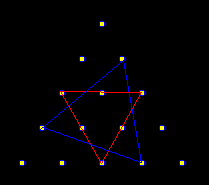
つまり、1辺の長さがmαの正三角形には、その正三角形を含めるとm個の正三角形ができます。
以上から、1辺にN個の点がある正三角形の中にできる正三角形の総和は
| N-1 Σ a=1 | (N+1−a)(N−a) ――――――――――― 2 |
a |
N=2の時 1個 N=3 5 N=4 15 N=5 35 N=6 70 N=7 126
【コメント】
N=4の時は、
1×(4×3)/2+2×(3×2)/2+3×(2×1)/2=15
N=5の時は、
1×(5×4)/2+2×(4×3)/2+3×(3×2)/2+4×(2×1)/2=35
N=6の時は、
1×(6×5)/2+2×(5×4)/2+3×(4×3)/2+4×(3×2)/2+5×(2×1)=70
というわけですよね。
なかなか美しい式ですね。
Σの式の計算方法は私はまだ確認していません。
◆広島県 清川 育男 さんからの解答。
N=2 1。 N=3 5。 N=4 15。 N=5 35。 N=6 70。 N=7。 126。正三角形の個数をSとする。
| S= | 1 ――― 24 | × | (N−1)N(N+1)(N+2) |
以上が予想されます。
今度は大丈夫だと思いますが、証明はまだです。
○補足
連続した4つの自然数の積は24の倍数であるから、Sは自然数になる。
【コメント】
これはgoya さんの答えとも一致しているし、正しいような気がします。
うまく証明できるのでしょうか?
◆石川県 マイマイプー さんからの解答。
Σの式の計算です。
| N-1 Σ a=1 | (N+1−a)(N−a) ――――――――――― 2 |
a |
| = | 1 ― 2 | × | N-1 Σ a=1 | (aN2-2a2N+aN-a2+a3) |
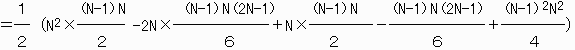
| = | 1 ――― 24 | × | (N−1)N(N2+3N+2) |
| = | 1 ――― 24 | × | (N−1)N(N+1)(N+2) |