◆石川県 谷井 正さんからの解答。
まず、一人目を見送ります。
そして、順番にお見合いを続けて、一番良い相手が出てきたらその人と結婚します。
残念ながら、一番良い人が現れなかったら最後の人と結婚します。
以上のようにすると、11/36の確率で最善夫と結婚できます。
人数が増えたら、おそらく最初の何%かを見送って、その後以前よりも良い人を選ぶのが正解だと思います。
感想:
私は35歳になるサラリーマンです。
数学は中学の頃から好きでした。
と言っても勉強が出来たわけではありません。
数学はクイズみたいなもので、解くことが楽しかった記憶があります。
ですから、このように遊びから数学が好きになってくれる子供が増えてくれれば良いと考えます。
今日は、初めてホームページを拝見しました。
残りもゆっくりと拝見させて頂きます。
【コメント】
こういう解答がくると私は本当にうれしいです。(^_^
思わず感想を全文載せてしまいました。
学校みたいにテストがあるわけではないですから、数学を純粋に楽しみましょう。
この作戦で完全な正解です。
しかし細かいことをいうと4人の並び方は4×3×2×1=24通りですから、
| 確率の正解は |
11 24 | ですね。 |
◆東京都 GOYAさんからの解答。
手順は石川県 谷井 正さんからの解答と同じです。
| 最善夫を選ぶ確率は |
11 24 | です。 |
| (計算式 |
1 4 | + |
1 8 | + |
1 12 | ) |
相手の数が8人の時は最初に見送る人数が3人で4人目以降で先の方法と同じように選びます。
この場合の最善夫を選ぶ確率は約41%です。
相手の数をn人、無条件にパスする人の数をp人とした時の最善夫を選ぶ確率は次式により、求められる。(と思います)
| Snp= |
p k | × |
n-1 Σ k=p |
1 k |
上記の式をどうやって導くかという説明は省きます。
というのも問題はこの先にもあってpをいくつにすればSが最大になるのかを計算式等で論理的に決定する方法が分らなかった(この為、Excelで計算しました)ことと、答えが間違っ
ているかも知れないからです。
論理的な解き方を検討される方の為にn=5~20の時のpとの対応を以下に記します。
上記の計算式が間違っていると正しい対応では無いことになりますが(^^;)
それと、転記ミスなども無いとは言い切れません。
| n | p | 確率 | n | p | 確率 |
| 5 | 2 | 0.4333 | 13 | 4 | 0.3907 |
| 6 | 2 | 0.4278 | 14 | 5 | 0.3917 |
| 7 | 2 | 0.4143 | 15 | 5 | 0.3894 |
| 8 | 3 | 0.4098 | 16 | 6 | 0.3881 |
| 9 | 3 | 0.4060 | 17 | 6 | 0.3873 |
| 10 | 3 | 0.3987 | 18 | 6 | 0.3854 |
| 11 | 4 | 0.3984 | 19 | 7 | 0.3850 |
| 12 | 4 | 0.3955 | 20 | 7 | 0.3842 |
【感想】
4人だと紙に書いて答えが出るのですが8人となるととてもじゃない(40,320通りもある)ですよね。
なもので、それなりに筋道立てて計算式を導いたのですが検証ができませんでした。
シミュレーションプログラムを作れば判るのですがプログラム言語ソフトを持ってないので。
【コメント】
全部確認することはちょっと無理だったのですが、確認した範囲では正しいような気がします。(^_^;
(自信なし)
ひょっとして力技で解くしかないのでしょうか。
だれか論理的な解答を作ってくれないかなぁー。
◆東京都 ニャンチャロフ さんからの解答。
カードがn枚あり、そのうちm枚を見送り、m+1枚目以降に、見送ったm枚中の最高額を超えるカードが出てき たら、その金額を受け取る、とした場合に、最高金額を受け取れる確率は、
1.
m+1番目のカードが最高金額の場合には、必ず最高金額を受け取れますから、確率は 1 です。
2.
m+2番目のカードが最高金額の場合には、m+1枚目のカードが、見送ったカードを含むm+1枚中で、最高額の
場合は失敗してしまいますから、
| 確率は、1- | 1 m+1 | = | m m+1 | です。 |
3.
m+3番目のカードが最高金額の場合には、m+1枚目のカードか、m+2枚目のカードが、見送ったカードを含むm
+2枚中で、最高額の場合は失敗してしまいますから、
| 確率は、1- | 2 m+2 | = | m m+2 | です。 |
4.
m+k+1番目のカードが最高金額の場合には、同様にして、
| 確率は、1- | k m+k | = | m m+k | です。 |
5.
最後のカードが最高金額の場合には、同様にして、
| 確率は、 | m n-1 | となります。 |
| ここで、任意のカードが最高額である確率は、それぞれ | 1 n | ですから、 |
| m n | *{ | 1 m | + | 1 m+1 | + | 1 m+2 | + | 1 m+3 | + ・・・ + | 1 n-1 | } になります。 |
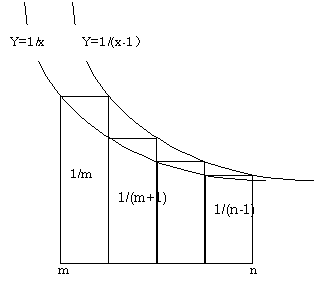
| 1 m | + | 1 m+1 | + | 1 m+2 | + | 1 m+3 | + ・・・ + | 1 n-1 | の部分に注目してください。 |
| この式の値は、関数 f(x)= | 1 x | が0<xでは減少関数ですから、 |
| n ∫ m |
1 x | dx = log(n)-log(m) = log( | n m | ) より大きく、 ・・・(1) |
| n ∫ m |
1 x-1 | dx = log(n-1)-log(m-1) = log( | n-1 m-1 | ) より小さいのです。・・・(2) |

ところで、最善の見送り枚数をmと仮定すると、勝率は、見送る枚数がmに達するまで増え続け、mを越えた時点から減り始めることになります。
したがって、
| m n |
n-1 ∑ k=m | 1 k | - | m-1 n | n-1 ∑ k=m-1 |
1 k | > 0 ・・・ (3) |
| m+1 n |
n-1 ∑ k=m | 1 k | - | m n | n-1 ∑ k=m |
1 k | < 0 ・・・ (4) |
(1)、(3) より、
| (3) = | 1 n | ( | n-1 ∑ k=m | 1 k | - 1)> | 1 n | { log( | n m | ) - 1} ≧0 |
log が増加関数であることに注意すれば、
| n m |
≧e すなわち m≦ | n e | ・・・ (5) |
(2)、(4) より、
| (4) = | 1 n | ( | n-1 ∑ k=m+1 | 1 k | - 1)< | 1 n | { log( | n-1 m | ) - 1} ≦0 |
log が増加関数であることに注意すれば、
| n-1 m |
≦e すなわち m ≧ | n-1 e | ・・・ (6) |
(5)と(6)の差は、1未満であり、mは自然数であることから、
| n-1 e |
≦m≦ | n e | を満たすm がある場合には、 |
そのような、m がない場合には、n/e をはさむ両側の自然数のどちらかが、最善となりますので、実際に計算
して比較します。
(もっといい方法があれば教えて)