◆広島県 清川 育男 さんからの解答。
1)少なくとも3つ公園が在ることの証明。
公園が2つしかないと仮定する。
そうすると条件3の全ての公園を通っている道はないということに矛盾する。
仮定に矛盾するから、少なくとも3つの公園があることになる。
次に3つの公園の位置関係を考える。
3つの道が3ヶ所で出会うように道があれば、条件1、条件2、条件3を満足する。
三角形の3つの頂点のように、このようになる3つの道は可能である。
2)公園が3つしかないと仮定する。
そうすると条件4により道Rが存在できない。
これは条件4に、矛盾する。
したがって少なくとも4つの公園が在ることになる。
次に4つの公園の位置関係を考える。
例えば、三角錐の4つの頂点に公園があるとすると、条件4の道Rは可能となる。
4つ目の公園は、小高い岡の上にあると考えられる。
【コメント】
公園を点、道を直線、街を平面と言い換えれば、わかりやすかったのではないでしょうか。
実は平面上でも4つの条件を満たすことは可能なのですが、岡の上にあるというのは面白いですね。
よろしかったら、平面上の例も見つけてください。
◆広島県 清川 育男 さんからの解答。
3つの公園で形成する三角形のなかに第4の公園があっても、道Rは可能ですね。
存在出来るエリアは、狭くなりますが。
◆東京都 ひろむ さんからの解答。
街=平面、公園=点、道=直線とした時、道が平行四辺形(頂点が公園)を描けば4の条件は満たせます。
ただ、この仮定において細かいことを言うと、定義に従って直線=長さ無限とした時、実際の街(地球上)はユークリッド平面ではなく、球面なのでいつか出合ってしまうかもしれませんが。
実際の道は曲線でも両端が行き止まりの線分でもありえるので、公園間を直線で結んだ形がどんな四角形でも4は満たせると思うのですが、それはヘリクツってやつでしょうか。
◆山梨県 Footmark さんからの解答。
【4つの公園の平面上の位置】
図では、6本の線が道で、線の交点が4つの公園になります。
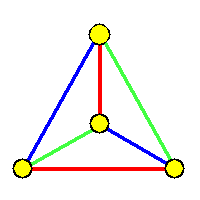
【数学者が「あなたの街には少なくとも4つの公園があるはずですね」と考えた理由】
論理的解法は清川さんが既に示されているので、その数学者が簡単な計算をしたものとして説明します。
「どの2つの公園をとってもその両方を通っている道が1本だけあります。」より、街にある公園の数がN個なら、道の数は
| NC2= | N(N−1) 2 |
に、なります。 |
そこで、逆に1つの道Rと出会う道を考えてみます。
道Rの両端にはそれぞれ1つずつ計2つの公園がありますが、道Rに出会う道とは、この2つの公園に至る道の筈です。
それぞれの公園において、自分以外の N−1 の公園と結ぶ N−1 の道があります。
ですから、道Rの両端の2つの公園では 2(N−1) あるはずですが、両公園を結ぶ道(道R)は2回数えているので
2(N−1)−1=2N−3に、なります。
1つの道Rに出会うことのない道の数は、すべての道の数から出会う道の数を除いてやれば良いので
| N(N−1) 2 |
−(2N−3) です。 |
一方、「道Rと出会わないような道が一つだけあります。」より
| N(N−1) 2 |
−(2N−3) =1 |
これを解くと、N=1 および N=4 になりますが、「街には、少なくとも2つの公園があります。」と「全ての公園を通っているような道はありません。」より、公園の数は3つ以上の筈ですから
N=4
つまり、街には4つの公園があることになります。
「2つの道が出会っている場所には必ず1つの公園があります。」より5つ以上の公園の場合は、道は立体交差にしなければなりませんが・・・
公園の数がNならば、1つの道Rに出会うことのない道の数は
| (N−2)(N−3) 2 |
になります。 |
公園の数が 3つ,4つ,5つ,6つ,7つ,8つ・・・で、出会うことのない道の数は 0,1,3,6,10,15・・・となります。
1番目と3番目の条件より、公園は3つ以上の筈ですが、3つでは4番めの条件を満たすのは不可能です。
ですから、数学者はそういった意味で、「それではあなたの街には少なくとも4つの公園があるはずですね。」
と、言ったけれど、計算が済んだ後ならきっと「それではあなたの街にある公園の数は4つですね。」と、言ったでしょう。