���C�O�̑�w���@Hirasawa Yasutaka����̉B
�@�@�@�@�@�iUniversity of North Carolina at Chapel Hill�j
X = 40 degree:
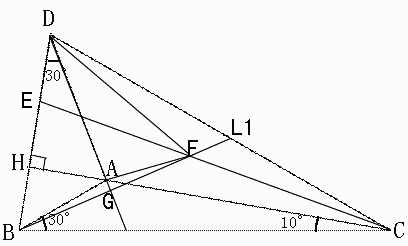
Set point E between D and H so that BH = EH.
CH is perpendicular to EB.
Thus, triangle CBE is isosceles and angle ECH = 10.
Draw a line (call it L1) so that extended DA is perpendicular to L1.
Call an intecept of L1 to CE as F.
Call an intercept of L1 to extended DA as G.
Now, angle HBC = 80. (consider a right angled triangle HBC)
angle DBG = 60. (consider a right angled triangle DBG)
Thus, angle GBC = 20 and angle ABG = 10.
Consider four points A, B, C, and F.
The fact that angles ABF = ACF ( = 10) implies These points are actually on the periphery of a circle.
Thus, angles AFB = ACB = 10.
This implies triangle ABF is isosceles.
Thus, BG = GF, i.e. DG intercept mid point of BF with a right angle.
Thus, triangle DBF is isosceles.
Especially it is an equilateral triangle since DBF = 60.
Thus, angle GDF = 30. Also, BF = DF.
Angle FBC = FCB ( = 20).
Thus, triangle FBC is isosceles.
Thus, BF = FC.
Thus, DF = FC, implying that triangle FCD is isosceles.
Angle DFE = 180 - angle EDF - angle DEF. (consider triangle DEF)
angle EDF = 60. and angle DEF = 100.
Thus angle DFE = 20.
Because triangle FCD is isosceles as shown before,2 * angle FDC = angle DFE = 20.
Thus, angle FDC = 10.
Finally, (huuuh....) angle X = GDF + FDC, thus X = 40.
I think this problem is the most challenging angle problem in your web page.
Took me about 2 days (maybe 1 hour each day) to find out above trick!
���ؖ��M�p���Ȃ��ł��������ˁB(^_^;
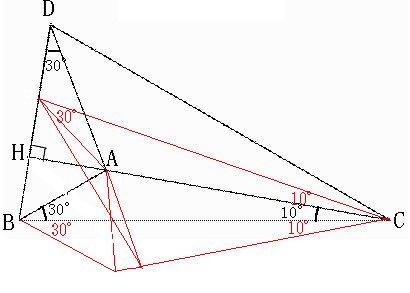
�����@�ڂ`�c�b�͂S�O�x
�_�d���c�Ƃg�̊ԂɁA�a�g���d�g�ɂȂ�悤�Ɏ��B
�b�g�͂d�a�ɐ����ł���B
���������āA���b�a�d�͓ӎO�p�`�Łڂd�b�g���P�O�x�B
�_�a���璼���i�k�P�ƌĂԁj���k�P�Ƃc�`�̉����������ɂȂ�悤�Ɉ����B
�k�P�Ƃb�d�̌�_���e�Ƃ���B
�k�P�Ƃc�`�̉����Ƃ̌�_���f�Ƃ���B
�Ƃ����
�ڂg�a�b���W�O�x�B (���p�O�p�`�g�a�b�Ȃ̂�)
�ڂc�a�f���U�O�x�B (���p�O�p�`�c�a�f�Ȃ̂�)
���������āڂf�a�b���Q�O�x�A�ڂ`�a�f���P�O�x�B
�S�_�`�C�a�C�b�C�e���l����B
�ڂ`�a�e���ڂ`�b�e�i���P�O�j�Ȃ̂ŁA�����̓_�͈�̉~����ɂ���B
���������āڂ`�e�a���ڂ`�b�a���P�O�x�B
���̂��Ƃɂ�聢�`�a�e�͓ӎO�p�`�B
���������Ăa�f���f�e�B
���Ȃ킿�c�f�͂a�e�𐂒��ɓ�����B
���������ā��c�a�e�͓ӎO�p�`�B
���ɁA�ڂc�a�e���U�O�x�Ȃ̂Ő��O�p�`�B
���������āڂf�c�e���R�O�x�B�܂��a�e���c�e�B
�ڂe�a�b���ڂe�b�a�i���Q�O�j
���������ā��e�a�b�͓ӎO�p�`�B
����Ăa�e���e�b�B
�����̂��Ƃ��c�e���e�b�Ȃ̂Ł��e�b�c�͓ӎO�p�`�B
�ڂc�e�d���P�W�O�|�ڂd�c�e�|�ڂc�d�e�i���c�d�e�ōl����j�B
�ڂd�c�e���U�O�x�B�ڂc�d�e���P�O�O�x�B
���������āڂc�e�d���Q�O�x�B
���e�b�c�͑O�q�̂悤�ɓӎO�p�`�Ȃ̂ŁA
�Q�~�ڂe�c�b���ڂc�e�d���Q�O�x�B
���������āڂe�c�b���P�O�x�B
�Ō�Ɂi�t�D�[�j
�ڂ`�c�b���ڂf�c�e�{�ڂe�c�b�B
���������āڂ`�c�b���S�O�x�B
���̖��͂��Ȃ��̃y�[�W�̒��ł����Ƃ���肪���̂���p�x�̖�肾�Ǝv���܂��B
���������̂ɂQ���Ԃ��炢�i�����炭�P���P���ԁj������܂����B

�y�R�����g�z
�@�݂��ƂS�O�K�Ő����ł��B
���̕⏕���͋C�����܂���ł����B
��͂�A�S�_�`�C�a�C�b�C�e����̉~����ɂ���Ƃ����̂��ؖ��̃|�C���g�Ȃ�ł��傤�ˁB
�������͂��̖��͓���~����ɂ���Ƃ��������g��Ȃ��ł������܂��B
���������Ē��w�Z�Q�N���ł��悭�l����Ή�����Ǝv���܂��B
�����ʂȉ��l�������������ł܂�����A���Ѓ��[���𑗂��Ă��������ˁB
�����@��T�ԔY��I�I�I ����̉B
�ڂc�`�g���U�O���Ȃ̂ŁA�c�`��_�`���牄�������������c�`���
�ڂ`�b�n���U�O���ƂȂ�_�n���Ƃ�ƁA���`�n�b�͐��O�p�`�ł���B
�i�ڂ`�b�n���ڂb�`�n���U�O�����j
����āA�ڂ`�n�b���U�O���ł���B
����ƁA������ڂ`�a�b���R�O���ł��邩��A
���S�p�ڂ`�n�b���U�O���ɑ��A�~���p�ڂ`�a�b���R�O���ƍl����A�~���p�̒藝�̋t�����藧�̂ŁA
�_�a�́A���S�n�Ŕ��a�n�b�i���邢�͂n�`�j�̉~����ɂ��邱�Ƃ�������B
���Ȃ킿�A���`�a�b�̊O�ډ~�̒��S�i�O�S�j���A�_�n�ł��邱�Ƃ�������B
����ƁA�ڂ`�n�a�́A�~���p�ڂ`�b�a���P�O���̒��S�p������A
�ڂ`�n�a���Q�O���ɂȂ�B
���ɁA�����n�a�ƒ����b�g�Ƃ̌�_���o�Ƃ���ƁA
���n�`�o�ɂ����āA�ڂn�`�b���U�O���͊O�p������A
�ڂn�o�`���ڂn�`�b�|�ڂ`�n�o���U�O���|�Q�O�����S�O���ɂȂ�B
����ƁA���a�`�o�ɂ����āA
�ڂa�o�`���S�O��
�ڂa�`�o���S�O��
�i���`�a�b�ɂ����āA�O�p�ڂa�`�o���ڂ`�a�b�{�ڂ`�b�a���j
�ł��邩��A���a�`�o�͓ӎO�p�`�ł���B
����ƁA������ڂa�g�`���X�O���ł��邩��A
�a�g�͂`�o�𐂒��ɓ����邱�Ƃ�������B
��������ƁA���c�o�`�͂c�o���c�`�̓ӎO�p�`�ɂȂ�A
�������A�ڂc�`�o���U�O���Ȃ̂ŁA���c�o�`�͐��O�p�`�ƂȂ�B
�
�����Ȃ�ƁA
���o�n�b�Ɓ��c�b�n�ɂ����āA
���c�o�`�����`�n�b�����O�p�`�ł��邩��A
�o�b���o�`�{�`�b���c�`�{�`�n���c�n�E�E�E(1)
�܂��A�n�b���b�n�i���ʁj�E�E�E(2)
�ڂo�b�n���ڂc�n�b���U�O���E�E�E(3)
����āA(1)�`(3)���A�Q�g�̕ӂƂ��̚�ފp�����ꂼ�ꓙ�����̂ŁA
���o�n�b�߁��c�b�n�ƂȂ�A�Ή�����p�͓������̂ŁA
�ڂ��i���ڂb�c�n�j���ڂn�o�b���S�O��
���ޗnj��̒��w�Z�P�N���@�땐 ����̉B
�`�g�̂g�̉�������ɂd�g���`�g�ƂȂ�悤�ɂd���Ƃ�B
���`�a�b�̊O�S���e�Ƃ���B
���e�`���e�a���e�b
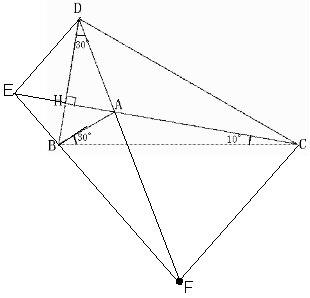
���`�c�g�Ɓ��c�d�g�ɂ����āA
�c�g���ʁA
�`�g���d�g�A
�ڂc�g�`=�ڂc�g�d���A
���`�c�g�߁��c�d�g�i�Q�Ӛ�p�j�ƂȂ�B
���`�c���c�d�ƂȂ�B
�ڂc�`�d��90-30��60�x���
�`�c���`�d���c�d�B(1)
��Ɠ��l�ɁA�a�d���`�a�ƂȂ�B(2)
�ڂ`�e�a�����A�ڂ`�e�b�����Ƃ��ĘA���������𗧂Ă��
|
180�|�� �\�\�\�\�\ 2 | �� |
180�|���|�� �\�\�\�\�\�\�\ 2 | +30 |
|
180�|�� �\�\�\�\�\ 2 | �� |
180�|���|�� �\�\�\�\�\�\�\ 2 | +10 |
����������ƃ���20�x�A����60�x�ƂȂ�B
�ڂ`�e�b��60�x�i�Β��p�j����̍�}��聢�`�b�e�́A���O�p�`�ł���B(3)
�܂��ڂ`�e�a��20�x�A�a�e���`�e���A
�@�ڂ`�a�e��80�x�B(4)
�ڂ`�a�b��30�x�A�ڂ`�b�a��10�x���
�@�ڂd�`�a��40�x�B(5)
(2)���ڂ`�a�d��180-40*2��100�x(6)
(4)(5)���ڂd�a�e��180�x
���d�A�a�A�e��3�_�͈꒼����ɂ���B
(1)(3)�ڂd�`�e���ڂc�`�b�i�Β��p�j���A
���d�`�e�߁��c�`�b�i�Q�Ӛ�p�j
���ڂ`�d�e���ڂ`�c�b
(2)(5)���A�ڂ`�d�e���S�O�x�B
����āڂ`�c�b���S�O�x
���z�F�d�A�a�A�e���꒼����ɂ���ǂ��ؖ��́A�����̂��ȁ`�B
���{�錧�@�A���p���}�� ����̉B
AH����HM��AH�̐����Ђ��B
��DAH���X�O-��HDA��60�x���灢DMA�͐��O�p�`�ł��B
��HAB=��ABC�{��ACB��40�x����
��HMB��40�x�B
��HBM=��HBA=90-��HAB=50�x�B
MB��DA�̌����_��N�A
��BAN=180-��BAH-��HAD=80�x�B
��ABN=180-��ABH-��HBM=80=��BAN
��BNA=180-��BAN-��ABN=20�x=2*��BCA
�����N�́�ABC�̉~�̃Z���^�[�ł��B
�܂�NA=NB��NC
��NAC����DAH��60�x���
��ANC�͐��O�p�`�䁢DMA
����ā�MNCD�͉~�ɓ��ڂ���l�p�`�ł��B
����������ADC��BMA��40�x�B
���É����@�����@�F�q ����̉B
���`�a�b���`�b�Ő܂�Ԃ��A���`�b�d����}����B
���̂Ƃ��A�d�͂g�c��ɂ���B
���ɁA���`�a�b���a�b�Ő܂�Ԃ��A���b�a�e����}����B
�����ŁA���b�a�d�͗���p�W�O���̓ӎO�p�`�A���`�a�e�͐��O�p�`�A���`�e�f�͗���p�W�O���̓ӎO�p�`�ł���ƌ�����B
���ɁA�c�`���������b�e�Ƃ̌�_���f�Ƃ���B
�ڂd�c�f���ڂd�b�f���R�O��������A�c�C�d�C�f�C�b�͓���~����̓_�ł���B
�䂦�ɁA�ڂb�f�c���ڂb�d�c���P�O�O���ł���B
���`�f�e�ɂ����āA�ڂ`�f�e���W�O�����ڂ`�e�f������A�ڂf�`�e���Q�O��
�ƂȂ�A�`�f���`�e�ł���B
���Ƃ��A�`�d���`�a���`�e������A�`�d���`�f�ł���B
�ڂd�`�f���P�U�O��������A�ڂ`�d�f���ڂ`�f�d���P�O���ł���B
�䂦�ɁA�ڂb�c�f���ڂb�d�f���R�O���{�P�O�����S�O��
���Ȃ킿�A�ڂ`�c�b���S�O���ł���B�i�I���j