
これを計算すると、

☆nが奇数の場合、 kは1から(n+1)/2まで変化させればよいから 求める正方形の個数は

これを計算すると、

◆Machida-City, Tokyo Akira Yamazaki(yuppie)さんからの解答。
思わず(朝になってるのに気づかず)、解いてしまいました。 >うーむ、すごい集中力だ。 「面積が1という条件をはずして、正方形の数を求める問題」を考えてみました。 やはり非常に難しい(面倒?)な問題でした。 解答: n段のとき作れる正方形の数は、 i) n = 2m-1 のとき m(4m2+3m-1)/6 個 ii) n = 2m のとき m(4m2+9m+5)/6 個 ( m = 1,2,3,... ) でした。 まず、考えたことは「どのようにすれば定性的に正方形の数を数えられるか」 ということです。これは以下の着想で意外に簡単に知ることができます。 _ . . |_|_ . . . / |_|_|_ . . . . // |_|_|_|_ . . . . . /// |_|_|_|_|_ . . . . . . //// |_|_|_|_|_| . . . . . . ///// Fig1 Fig2 Fig3 まず、Fig1のような階段があるとすると、その格子点を考える(Fig2)。 この格子点から、作ろうとする正方形の「対角線を構成する2点」を選べば良 い。ここで、対角線はFig3のようにとれば間違いなく正方形のみを構成するこ とができる。たとえばFig4のような点集合( 。)を選んだとする。 . . . . . . . . 。 . . 。 . . . 。 . . . . 。 . . . . . Fig4 この点集合から作られる正方形(の対角線)の数は4つから2つをとる組合わせの 数であり、((m,n)は、ここでは組合わせの数(combination)を表す) (4,2) = 4*3/2! = 6 通りである。このようにしてすべての点を「斜めに」数えて、そこから2つを とる組合わせの数を計算し、合計すれば望む答えが得られるはずである。 さて、次にn段のときのFig4のような特定の「斜めの列」の点の数を定性的に 表さなければならない。Fig4であれば、斜めの列の点の数は上から、 2個 2個 3個 3個 4個 3個 3個 2個 2個 である。この数を合計してはいけない。それぞれの数に対して(*,2)を計算し なければならないからである。この数字の配列(数列)は階段の数に応じて以下 のようになっている。 1段 2 2段 2 2 2 3段 2 2 3 2 2 4段 2 2 3 3 3 2 2 5段 2 2 3 3 4 3 3 2 2 ( <- Fig4 ) 6段 2 2 3 3 4 4 4 3 3 2 2 : : これらから数列a(n)をn段のときに存在する正方形の数とすれば、 a(n) = a(n-1) + ( [(n-1)/2]+1 , 2 ) + ( [n/2]+1 , 2 ) , a(1)=1,a(2)=3 となっていることが分かる。ただし、[n]はnを四捨五入した数であり、(m,n) は先ほどと同じくmからnをとる組合わせの数である。 ここまで分かれば n=2m-1 と n=2m の場合わけて数列の一般項を求めれば良い。 (さすがに中学生では、解くのは無理でしょうね。) ということで、これを解くと, a(2m-1) = m(4m2+3m-1)/6 …(1) a(2m) = m(4m2+9m+5)/6 ( m = 1,2,3,... ) …(2) となりました。おそらくこれは正しいでしょう。ちなみに、 n=1 つまり m=1で(1)のとき a(1)=1 n=2 つまり m=1で(2)のとき a(2)=3 n=3 つまり m=2で(1)のとき a(3)=7 n=4 つまり m=2で(2)のとき a(4)=13 n=5 つまり m=3で(1)のとき a(5)=22 n=6 つまり m=3で(2)のとき a(6)=34 : n=9 つまり m=5で(1)のとき a(9)=95 n=10つまり m=5で(2)のとき a(10)=125 となりました。(n=6以上は数えてないのであってるか分かりませんが^^;) -- 感想 -- うーむ。つかれた....暇なときにはひじょーにいい刺激になりますね。
【コメント】
私も責任上すべて確認しました。
まちがいなく、正解です。
最初の問題(1)、(2)を作った生徒は呆然とするでしょうね。
私自身ひさしぶりに、よい勉強になりました。
そのうちまた暇をつぶせる?問題を出題しますね。
◆神奈川県 sharimaさんからの解答。
n段における面積hxhの正方形の数を求める方法は次のようになります。
| 1+2+3+・・・+ | n−h+1 h |
従って,
| 面積1の正方形の数は | n(n+1) 2 | です。 |
| n−h+1 h | は整数である必要があるから, |
例えば
面積2x2(4)の数は,1+2+・・・・ (n−1)/2
3x3(9) 1+2+・・・・ (n−2)/3
4x4(16) 1+2+・・・・ (n−3)/4
・
・
・
そしてnが決まれば,各面積hxhの正方形の数は上の各個数を加えればよい。
面積1の数は,(n−h+1)/h=10ですから全部で 55個
2x2 , =4.5 → 4 10個
3x3 =2.66 → 2 3 個
4x4 =1.75 → 1 1 個
5x5 =1.2 → 1 1 個
6x6 =0.83 → 0
合計 70個
【コメント】
私は最初は解答の意味がわからなかったのですが、sharimaさんにお聞きしてわかりました。
正方形が重なる場合がないとしての解答だったのですね。
問題の意味が分かりにくくてすいません。
重なった部分があっても別の正方形として数えてください。
重複を許さないとすれば、70個で正解です。
◆石川県 マイマイプーさんからの解答。
神奈川県 sharimaさんからの解答がヒントになりました。
面積1(つまり1辺1)の正方形の個数は 1からnまでの和 面積4(つまり1辺2)の正方形の個数は n=4→1+2 n=5→1+2+3 n=6→1+2+3+4 つまり、1からn−2までの和。 面積9(つまり1辺3)の正方形の個数は n=5→1 n=6→1+2 n=7→1+2+3 つまり、1からn−4までの和 一般に面積k2(一辺k)の正方形の個数は 1+2+・・・+{n−2(k−1)} ☆nが偶数の場合、 kは1からn/2まで変化させればよいから 求める正方形の個数は
これを計算すると、
☆nが奇数の場合、 kは1から(n+1)/2まで変化させればよいから 求める正方形の個数は
これを計算すると、
【コメント】
この解答で面白いのは、当然なのかもしれませんが、
| 奇数と偶数の場合の答えの差が | 1 8 |
になったことです。 |
| 1 12 | n3+ | 3 8 |
n2+ | 5 12 | n+ | 1 16 |
+ | (-1)n+1 16 |
とでもすれば両者を統一できそうですね。
◆山梨県 Footmark さんからの解答。
マッチ棒の1つの交点に任意の大きさの正方形の右上の角がある時、正方形の左下の角がとり得る点は、その交点から斜め左下方向にある交点です。
これらの交点の数こそが、特定した1つの交点に正方形の右上の角がある時の、任意の大きさの正方形の数の筈です。
8段を例に、各−の交点に右上の角がくる正方形の数を、その交点に記入すると以下になります。
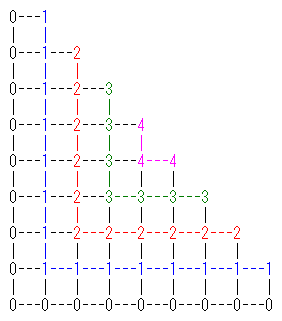
1x1の正方形を積み上げていくのですから、交点に1以上が記入されている箇所だけが問題になります。
ですから、1番左と1番下は除いて、交点に記入された数字だけを図で表すと以下になります。
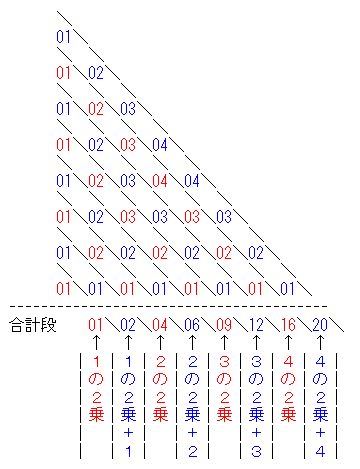
1x1の正方形をn段積み重ねた時のすべての正方形の数は、上図の合計段の数列の1番目からn番目までの総和になります。
数列の1番目からn番目までの総和をS(n)で表すと、
| ◆ nが偶数の時は、 | n 2 |
=m とすると |
| S(n)=2{ | m(m+1)(2m+1) 6 |
}+ | m(m+1) 2 |
| ここで、m= | n 2 |
に戻すと |
S(n)
| = | n(n+1)(n+2) 12 |
+ | n(n+2) 8 |
| = | 2n3+9n2+10n 24 |
| = | n(n+2)(2n+5) 24 |
| ◆ nが奇数の時は、 | n+1 2 |
=m とすると |
| S(n)=2{ | m(m+1)(2m+1) 6 |
}+ | m(m+1) 2 | −m(m+1) |
| ここで、m= | n+1 2 |
に戻すと |
S(n)
| = | (n+1)(n+2)(n+3) 12 |
+ | (n+1)(n+3) 8 |
− | (n+1)(n+3) 4 |
| = | 2n3+9n2+10n+3 24 |
| = | n(n+2)(2n+5) 24 | + | 1 8 |
◆ nが偶数の時と奇数の時を統合した一般式は
| S(n)= | n(n+2)(2n+5) 24 | − | (−1)n−1 16 |
1x1の正方形を10段目まで積み上げたのなら、
S(10)
| = | 10(10+2)(2x10+5) 24 |
− | (−1)10−1 16 |
| =125 |
任意の正方形は125個あります。