仧暫屔導丂昹忋 惓巎偝傫偐傜偺夝摎丅
嶼悢揑側夝摎偱怽偟栿偁傝傑偣傫丅
捈曽懱偺棤偵偼摴偼側偄傕偺偲偟偰峫偊傑偡丅
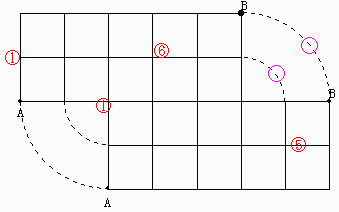
乮侾乯
丂俙揰偐傜俀偺曽岦傊俀偮恑傫偩揰傪俢揰偲偟傑偡丅
丂俢揰偐傜侾偺曽岦傊侾偮恑傫偩揰傪俤揰偲偟傑偡丅
丂俤揰偐傜侾偺曽岦傊侾偮恑傫偩揰傪俥揰偲偟傑偡丅
丂俥揰偐傜侾偺曽岦傊侾偮恑傫偩揰傪俧揰偲偟傑偡丅
丂俧揰偐傜侽偺曽岦傊侾偮恑傫偩揰傪俫揰偲偟傑偡丅
丂俙揰偐傜俢揰傑偱峴偔偵偼丂俀俀丂偺侾偲偍傝
丂俢揰偐傜俛揰傑偱偼
丂丂丂丂侾侾侾侽侽丆 侾侾侽侾侽
丂丂丂丂侾侾侽侽侾丆 侾侽侾侾侽
丂丂丂丂侾侽侾侽侾丆 侾侽侽侾侾
丂丂丂丂侽侾侾侾侽丆 侽侾侾侽侾
丂丂丂丂侽侾侽侾侾丆 侽侽侾侾侾丂偺侾侽偲偍傝
仸乮俆偺弴楍亐乮俁偺弴楍亊俀偺弴楍乯乯偱傕侾侽偲偍傝偲寁嶼偱偒傑偡
丂傛偭偰丄俙揰偐傜俢揰傪捠傝俛揰偵偄偔応崌偼
丂侾亊侾侽亖侾侽偲偍傝
丂俙揰偐傜乮俢揰傪捠傜側偄偱乯俤揰偵偄偔偵偼丂侾俀俀丄俀侾俀丂偺俀捠傝
丂俤揰偐傜俛揰偵峴偔偵偼
丂丂丂丂侾侾侽侽丆 侾侽侾侽
丂丂丂丂侾侽侽侾丆 侽侾侾侽
丂丂丂丂侽侾侽侾丆 侽侽侾侾丂偺俇偲偍傝
仸乮係偺弴楍亐乮俀偺弴楍亊俀偺弴楍乯乯丂偱傕俇偲偍傝偲寁嶼偱偒傑偡
丂傛偭偰丄俙揰偐傜乮俢揰傪捠傜側偄偱乯俤揰傪捠傝俛揰偵偄偔応崌偼
丂俀亊俇亖侾俀偲偍傝
丂俙揰偐傜乮俢丆俤揰傪捠傜側偄偱乯俥揰偵偄偔偵偼丄
丂丂丂丂侾侾俀俀
丂丂丂丂侾俀侾俀
丂丂丂丂俀侾侾俀偺俁偲偍傝
丂俥揰偐傜俛揰偵峴偔偵偼
丂丂丂丂侾侽侽丆 侽侾侽
丂丂丂丂侽侽侾丂偺俁偲偍傝
丂傛偭偰丄俙揰偐傜乮俢丆俤揰傪捠傜側偄偱乯俥揰傪捠傝俛揰偵偄偔応崌偼丄
丂俁亊俁亖俋偲偍傝
丂俙揰偐傜乮俢丆俤丆俥揰傪捠傜側偄偱乯俧揰偵偄偔偵偼
丂丂丂丂侾侾侾俀俀丆 侾侾俀侾俀
丂丂丂丂侾俀侾侾俀丆 俀侾侾侾俀丂偺係偲偍傝
丂俧揰偐傜俛揰偵峴偔偵偼丂侽侽丂偺侾偲偍傝
丂傛偭偰丄俙揰偐傜乮俢丆俤丆俥揰傪捠傜側偄偱乯俧揰傪捠傝俛揰偵偄偔応崌偼丄
丂係亊侾亖係偲偍傝
丂俙揰偐傜乮俢丆俤丆俥丆俧揰傪捠傜側偄偱乯俫揰偵偄偔偵偼
丂丂丂丂侾侾侾侽俀俀丆 侾侾侾俀侽俀
丂丂丂丂侾侾俀侾侽俀丆 侾俀侾侾侽俀
丂丂丂丂俀侾侾侾侽俀丂偺俆偲偍傝
丂俫揰偐傜俛揰偵峴偔偵偼丂侽丂偺侾偲偍傝
丂傛偭偰丄俙揰偐傜乮俢丆俤丆俥丆俧揰傪捠傜側偄偱乯俫揰傪捠傝俛揰偵偄偔応崌偼
丂俆亊侾亖俆偲偍傝
丂丂丂丂侾侾侾侽侽俀俀丆侾侾侾侽俀侽俀
丂丂丂丂侾侾侾俀侽侽俀丆侾侾俀侾侽侽俀
丂丂丂丂侾俀侾侾侽侽俀丆俀侾侾侾侽侽俀丂偺俇偲偍傝
丂丂丂丂丂丂摎偊丂係俇偲偍傝
乮俀乯丂丂
丂丂丂丂侾侾侾侽侽俀俀丆侾侾侾侽俀侽俀
丂丂丂丂侾侾侾侽俀俀侽丆侾侾侾俀侽侽俀
丂丂丂丂侾侾侾俀侽俀侽丆侾侾侾俀俀侽侽
丂丂丂丂侾侾俀侾侽侽俀丆侾侾俀侾侽俀侽
丂丂丂丂侾侾俀侾俀侽侽丆侾侾俀俀侾侽侽
丂丂丂丂侾侾俀俀侽侾侽丆侾侾俀俀侽侽侾
丂丂丂丂摎偊丂侾俀偲偍傝
乮俁乯
丂丂丂丂俁俇亊侾亖俈俀俋
丂丂丂丂俁俆亊侾亖俀係俁
丂丂丂丂俁係亊侾亖俉侾
丂丂丂丂俁侾亊俀亖俇
丂丂丂丂俁侽亊俀亖俀
丂丂丂丂崌寁丂侾侽俇侾
亂僐儊儞僩亃
丂偡偽傜偟偄夝摎偁傝偑偲偆偛偞偄傑偡丅
偒偪傫偲偟偨応崌暘偗偼戝曄悢妛揑偩偲巚偄傑偡丅
懠偺傗傝曽傪峫偊偨曽偼儊乕儖偔偩偝偄偹丅
丂偲偙傠偱丄偙偺夝摎傪傕傜偭偰偐傜
乮係乯傕偟丄捈曽懱偺掙柺偵傕摨偠傛偆偵摴偑偁傞偲偡傞偲丄乮侾乯丆乮俀乯偺摎偊偼偳偺傛偆偵側傞偐丅
偲偄偆栤戣傪捛壛偟傑偟偨丅彮偟曄傢傞偲巚偆偺偱偡偑偳偆偱偟傚偆偐丅
娙扨偵側傞偺偐丄擄偟偔側傞偺偐丠丅傑偨挧愴偟偰傒偰偔偩偝偄偹丅
仧悢妛岲偒偺偍偠偝傫偙偲恄撧愳導丂sharima丂偝傫偐傜偺夝摎丅
捈曽懱偺掙柺偵傕摨偠傛偆偵摴偑偁傞応崌偺夝摎偑偝偭偦偔偒傑偟偨丅
乮侾乯偺夝摎
偙傟偼壓椺偺傛偆偵丆侽丆侾丆偍傛傃俀偐傜側傞俈寘偺悢偱丆侽偑俀屄丆侾偑俁屄丆俀偑俀屄偺慻傒崌傢偣偺悢偵摍偟偄偲巚偄傑偡丅
慠偟側偑傜丆摎偼帪娫偑妡傝偦偆偱暘偐傝傑偣傫偱偟偨丅
妋偐偙傟傪夝偔幃偑嵼傞偲婰壇偟偰偄傑偡丅
丂椺丂侽侽侾侾侾俀俀丆侽侽侾侾俀侾俀丆侽侽侾侾俀俀侾偐傜丒丒丒丒丒俀俀侾侾侾侽侽傑偱
乮俀乯偺夝摎
摨條偵丆侽丆侾丆偍傛傃俀偐傜側傞俆寘偺悢偱丆侽偑俀屄丆侾偑侾屄丆俀偑俀屄偺慡慻崌偣偺悢偵摍偟偄丅
侽侽侾俀俀丆侽侽俀侾俀丆侽侽俀俀侾偐傜丒丒丒丒丒俀俀侾侽侽傑偱
亂僐儊儞僩亃
丂偙傟偼偡偽傜偟偄傾僀僨傿傾偱偡偹丅
巹傕仜仜擭慜偺崅堦偺嶲峫彂傪扵偟偰偟傑偄傑偟偨丅
暯柺偺応崌偼偦傟偱惓夝偩偲巚偄傑偡丅
偨傇傫岞幃偼丄椺偊偽乮侾乯偱偼
俈両乛乮俀両亊俁両亊俀両乯亖俀侾侽捠傝
乮両偼奒忔偺婰崋偱偡丄椺偊偽俁両亖俁亊俀亊侾乯
偱傕側偤偐懡偡偓傑偡偹丅
巹傕嬻娫偱傕惓偟偄偺偐偲巚偭偨偺偱偡偑丄戝曄側偙偲偵婥偑偮偒傑偟偨丅
椺偊偽乮侾乯偱偼丄侾丆侽丆俀丒丒丒偲偄偭偨僷僞乕儞偼捈曽懱偺拞偵擖偭偰偟傑偆偺偱丄偁傝偊側偄偺偱偼側偄偱偟傚偆偐丅
偙偺傾僀僨傿傾傪敪揥偝偣偰丄偤傂惓夝傪尒偮偗偰偔偩偝偄丅
懠偵傕夝偗偨曽偑偍偄偱傑偟偨傜丄儊乕儖傪偍懸偪偟偰偄傑偡丅
仧嫗搒晎丂姌嶁丂惓朏丂偝傫偐傜偺夝摎丅
乽昹忋偝傫偺夝摎乿偼嵍懁偺柺乮恾偱偼尒偊偰側偄乯偐傜偺宱楬偑敳偗偰偄傞傛偆偱偡丅
寁嶼偱弌偡応崌丆掙柺偵傕摴偑偁傞栤係偺曽偑娙扨側偺偱丆傑偢偙偪傜偐傜丅
乮係乯偺夝摎
侽丆侽丆侾丆侾丆侾丆俀丆俀丆偺暲傋懼偊偰偱偒傞弴楍偺悢偼
俈両亐乮俀両亊俁両亊俀両乯
亖俀侾侽乮捠傝乯丂丂仸
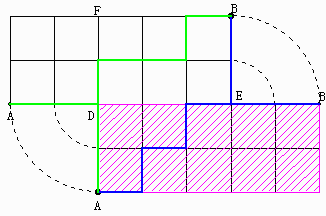
傕偲偺恾宍傪棫曽懱偺廤傑傝偲峫偊傞偲丆棫懱撪晹偵棫曽懱偺捀揰偑廤傑偭偨俀揰
乮俹乮俙偵嬤偄曽乯丆俻乯偑懚嵼偟丆偙偺俀揰傪捠傞宱楬偺悢傪堷偔昁梫偑偁傝傑偡丅
俙偐傜俛傊峴偔宱楬偺悢丆俙偐傜俹傪宱桼偟偰俛傊峴偔宱楬偺悢傪偦傟偧傟
俶乮俙丆俛乯丆俶乮俙丆俹丆俛乯偲昞偡偙偲偵偟傑偡丅
俶乮俙丆俹乯偼侽丆侾丆俀偺弴楍丆
俶乮俹丆俛乯偼侽丆侾丆侾丆俀偺弴楍偵側傝丆
俶乮俙丆俹乯亖俁両亖俇
俶乮俹丆俛乯亖係両亐俀両亖侾俀
偟偨偑偭偰丆丂
俶乮俙丆俹丆俛乯亖俶乮俙丆俹乯亊俶乮俹丆俛乯亖俈俀
傑偨丆懳徧惈偐傜丆
俶乮俙丆俻丆俛乯亖俶乮俛丆俻丆俙乯亖俈俀
偟偐偟丆俹丆俻偺椉曽傪捠傞宱楬傪俀廳偵悢偊偰偄傞偺偱丆堷偔昁梫偑偁傝傑偡丅
俶乮俙丆俹丆俻丆俛乯
亖俶乮俙丆俹乯亊俶乮俹丆俻乯亊俶乮俻丆俛乯
亖俇亊侾亊俇
亖俁俇
傛偭偰
俀侾侽乗乮俈俀亄俈俀乗俁俇乯亖侾侽俀乮捠傝乯
乵拞妛惗偺傒側偝傫偵丂仸偺幃偺愢柧乶
廳暋弴楍偲偄偭偰丆偙偺岞幃偼崅峑偱廗偄傑偡偑丆偙偺岞幃傪巊傢側偄峫偊曽傪娙扨偵愢柧偟傑偡丅
仩仩仩仩仩仩仩偺俈偮偺儅僗偵乽侽乿傪侾偮擖傟傑偡丅
擖傟曽偼俈捠傝偱偡丅
師偵傕偆侾偮偺乽侽乿傪擖傟傑偡丅
擖傟曽偼俇捠傝偱偡丅
壖偵侾偮栚傪俁斣栚丆俀偮栚傪俇斣栚偵偄傟偨応崌丆
仩仩侽仩仩侽仩偺傛偆偵側傝傑偡丅
偟偐偟丆侾偮栚傪俇斣栚丆俀偮栚傪俁斣栚偵擖傟偨応崌傕慡偔摨偠偵側傝傑偡丅
偟偨偑偭偰丆乽侽乿偺擖傟曽偼丆
俈亊俇亐俀亖俀侾乮捠傝乯偵側傝傑偡丅
偮偓偵丆巆傝偺俆偮偺儅僗偵俀偮偺乽俀乿傪擖傟傞傢偗偱偡偑丆摨偠傛偆偵峫偊偰丆
俆亊係亐俀亖侾侽乮捠傝乯偵側傝傑偡丅
巆偭偨儅僗偼俁偮偱偡偐傜丆偦偙偵乽侾乿傪擖傟傑偡丅
傕偪傠傫丆侾捠傝
俀侾亊侾侽亊侾亖俀侾乮捠傝乯偲側傝傑偡丅
弴楍丒慻崌偣偼丆傑偩抦傜側偄偲巚偄傑偡偑丆慻崌偣偺婰崋偱彂偔偲
7俠2亊5俠2亊3俠3丂偲側傝傑偡丅
傑偨丆乽侾乿傛傝偝偒偵乽俀乿傪擖傟偨偺偼丆偙偺曽偑娙扨偩偐傜偱偡丅
偄偮偱傕偙偆偄偆岺晇傪偡傞傛偆偵丆偟偰偔偩偝偄丅
乮侾乯 偺夝摎
掙柺偵摴偑側偄応崌偱偡偑丆俹丆俻偺壓偺俀揰傕捠傟側偄偙偲偵側傝傑偡丅
偮傑傝丆係揰偺偆偪丆彮側偔偲傕侾揰傪捠傞宱楬偺悢傪俀侾侽偐傜堷偗偽傛偄偺偱偡偑丆応崌暘偗偑偐側傝戝曄偵側傝傑偡丅
偦偙偱丆暿偺曽朄傪峫偊傑偡丅
墱偺柺傪捠傞偲墦夞傝偵側傝傑偡偐傜丆偦傟埲奜偺柺偺揥奐恾傪峫偊傑偡丅

嘆 庤慜偺柺偲塃懁偺柺乮僺儞僋偺幬慄晹暘乯傪捠偭偰俙偐傜俛傊偺宱楬偺悢偼
塃丆塃丆塃丆塃丆塃丆忋丆忋偺弴楍偺悢偲摨偠偵側傝傑偡偐傜丆
俈亊俇亐俀亖俀侾乮捠傝乯偵側傝傑偡丅
嘇 庤慜偺柺偲忋偺柺傪捠傞宱楬偺悢偼丆
塃丆塃丆塃丆忋丆忋丆忋丆忋偺弴楍偺悢偲摨偠丅
俈亊俇亊俆亐乮俁亊俀亊侾乯亖俁俆乮捠傝乯
嘊 嵍懁偺柺偲忋偺柺傪捠傞宱楬偺悢偼丆嘆偲摨偠偱丆俀侾捠傝
偟偐偟丆惵偄慄偱帵偡傛偆側宱楬偼嘆偲嘇偱擇廳偵悢偊偰偄傑偡丅
偙偺宱楬偺悢偼
俶乮俙丆俤乯亖俆亊係亐俀亖侾侽乮捠傝乯
摨條偵椢偺慄偱帵偡傛偆側宱楬傕嘇偲嘊偱擇廳偵悢偊偰偄偰丆
偍側偠偔丂俶乮俢丆俛乯亖侾侽乮捠傝乯
偟偨偑偭偰丆偡傋偰偺宱楬偺悢偼丆
俀侾亄俁俆亄俀侾乗侾侽乗侾侽亖俆俈乮捠傝乯
亂尨巒揑偩偑堄奜偵巊偊傞夝朄亃
拞妛庴尡傪偟偨宱尡偺偁傞恖側傜抦偭偰偄傞偲巚偄傑偡偑丆偁傞奿巕揰乮岎嵎揰乯偵偼丆嵍偐傜偲丆壓偐傜棃傞偙偲偑弌棃傞偺偱丆偦偺悢帤傪壛偊偰偄偔偲偄偆曽朄偱偡丅
椺偲偟偰俙偐傜俤傊峴偔応崌傪帵偟傑偡丅
椺偊偽揰俿偺応崌丆嵍偐傜偺侾偲壓偐傜偺俀偱俁偵側傝傑偡丅
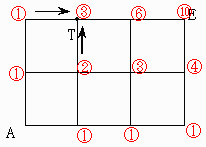
愭偵崅峑偱廗偆岞幃仸傪彂偒傑偟偨偑丆捠傟側偄揰偑偁傞栤戣側偳偼丆仸偺岞幃傪巊偆傛傝丆尨巒揑偲巚偊傞偙偺曽朄偺曽偑憗偄偲偒偑偁傝傑偡丅
偙偺栤戣乮係乯傕堦斣憗偄偐傕抦傟傑偣傫丅
偨偩丆棫懱偵側偭偰傑偡偐傜丆嵟弶偲丆嵟屻偺曽偼丆乮摿偵仜偺晹暘乯偼拲堄偡傞昁梫偑偁傝傑偡丅
晹暘揑偵悢帤傪擖傟偰偍偒傑偡偐傜丆揰慄偱寢傫偱偁傞揰偼摨偠揰偱偁傞偙偲偵拲堄偟偰傗偭偰傒偰壓偝偄丅
偳偆偱偡丠娙扨偱偟傚偆丅