◆栃木県の群馬県子持村子持村立子持中学校から寄せられた解答
3年生の選択数学の授業から
「玉が最後に入る場所」について・・・・解答者2名
(縦、横)を最も簡単な比に直したとき、
(偶数、奇数)の時は、右上の頂点で止まる。
(奇数、奇数)の時は、右下の頂点で止まる。
(奇数、偶数)の時は、左下の頂点で止まる。
*(偶数、偶数)は最も簡単な比に直すため、考えられないので上に示した3通りである。
「玉が壁にバウンドする回数」について・・・・解答者3名
(縦、横)を最も簡単な比に直し、その2つの数の和から1を引いた数が壁にバウンドした数となる。
【コメント】
すばらしい解答ですね。
一時間の授業でここまでできたというのはすごいですね。
それでは、なぜそうなるのか理由を考えてみてください。
◆栃木県の45歳のおじさんからの解答
2週間前に一度見たのですがまだ回答が増えていなかったので、おじさんが 出てくるのはいけないかなと思いましたが、私の答を送ります。
>いえ、いえ、とんでもありません。
>大歓迎です。
たいへんアバウトな書き方になると思いますが申しわけありません。
だいたいこの手の反射の問題は、反射しないで直進することにして、空間の方を鏡面コピーしていくのかな。
そうすると玉は45度で直進して行くだけで、結局角にあたって止まるとは最後に鏡面コピーした長方形の右下に来ることだから、45度だから全体は大きな正方形の空間になって終わる。
ということは、畳のタテヨコ比がへんてこな百畳敷きの大宴会場を新入社員がビールを
取りに斜めに走っていく・・・みたいなもんか (^_^;、
で、縦も横も、最初の長方形のタテヨコの最小公倍数になるから、
あ、出来た、百畳敷きの畳の縦の境界線と横の境界線を全部横切るから、
タテヨコの畳の枚数の和から、出発点とゴールの二つを引いたのが答。
【コメント】
いやぁー、この解答は中学生には書けません。
でも大変分かりやすいですね。
私はあわれな新入社員を想像してしまいました。
ユニークな解答、ありがとうございました。
◆栃木県の中学校3年生 大島 朋幸さんからの解答。
この問題は、やり始めは難しかったけど、やり始めたら結構わかりやすい問題だったと思います。
やっていてとても、おもしろかったです。
やったかいがありました。
<回答>
玉が止まるまでの回数は、縦の長さと横の長さをたして、それから2を引いてだします。
縦の長さ+横の長さ−2=玉が止まるまでの回数
1 + 1 −2= 0
1 + 2 −2= 1
1 + 3 −2= 2
1 + 4 −2= 3
2 + 5 −2= 5
3 + 7 −2= 8
4 + 9 −2= 11
5 +10 −2= 13
こんな風に玉が止まる回数をだします。
ただし、1つだけ注意しなければいけないところがあります。
それは お互いに割り切れる数字の場合があります。
例えば
2 + 4 −2= 1
4 + 6 −2= 3
6 + 14 −2= 8
15 + 25 −2= 6
などのように、お互い割り切れる場合は最大公約数で割ってだします。
2 + 4 −2= 1
は、2が最大公約数だから
1 + 2 −2= 1
と同じになります。
例では 小さい数しかだしていませんが大きい数でもちゃんとでてきますよ。
自分でやってみればすぐにわかりますよ。
これで、僕の考えた回答の説明は終わりです。
【コメント】
すばらしい分析ですね。
最初に、最大公約数が1の時の関係に気がついたのですか?。
そこから一歩進んで、最大公約数が1でない場合の関係を見つけられたのがすごいです。
最後に玉が入る位置と、縦横の長さの関係もぜひ考えてみてくださいね。
◆石川県 Takashiさんからの解答。
横幅をx、縦幅をyとする。【x,yは自然数】
x,yの最小公倍数をzとするとき、z=p・x=q・y となる。
【p,qは互いに素な自然数】
今、ボールがスタートして左右の壁にp回目に当たる時、ボールは左右方向にp・x=z移動していることになる。
ボールは常に壁に対して45°の角度を保ったまま移動しているので、この時上下方向にもz移動している。
z=q・y だから、ボールが左右の壁にp回目に当たるのと同時に上下の壁にもq回目に当たろうとしている。
つまりボールは角に当たるわけなので、そのときボールがとまる。
壁に当たる回数は、最後の角に当たる時を除いて、(p+q−2)回。
ボールが止まる角について、
<感想>
この問題を見て、初めはボールが壁に当たる点を(x(j),y(j))として一つずつ追跡しようとしていましたが、この解法を思いついて、最初の考え方の無駄の多さに呆れてしまいました。
◆京都府 釜坂 正芳 さんからの解答。
もとのビリヤード台ABCDを折り返して正方形を作ります。
「栃木県のおじさん」のいう「百畳敷き」の正方形をつくるわけですが,百畳敷きの図はつらいので,
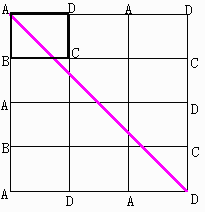
縦:横=3:4の場合が次の図です。

縦に4枚,横に3枚並んだ正方形になり,線分ADが玉の進路になります。
「対角線の問題」と双子問題であることが分かります。
(3−1)本の縦線,(4−1)本の横線と交わり,5回跳ね返ることが分かります。
さて到達点ですが,下辺と右辺の記号に注意して下さい。
下辺にはAとDが,右辺にはDとCが並び,共通するDに到達しています。
それでは,一般の場合を考えます。
縦と横の長さの最も簡単な整数比を
p:q(当然互いに素)とします。
最も小さい正方形を作ると,縦にq枚,横にp枚並びますから
跳ね返る回数は
(p−1)+(q−1)=p+q−2 となります。
下辺は
qが偶数のとき A,D
qが奇数のとき B,C
右辺は
pが偶数のとき A,B
pが奇数のとき D,Cとなり
p,qは互いに素であるから次の3つの場合
pが偶数,qが奇数のとき Bに到達
pが奇数,qが偶数のとき Dに到達
pが奇数,qが奇数のとき Cに到達
◆埼玉県 masaru2002 さんからの解答。
※GCF(x,y)はxとyの最大公約数を表すものとする。
今、縦・横の長さq,p∈Nが与えられたとき、
| a= | p GCF(p,q) | ,b= | q GCF(p,q) | とする。 |
わかりやすくするために、縦方向を入れ替えて考える。
座標系を用いて一般化して表せば、
P=(na,mb)で(※下図参照)
点Pは直線y=λx上に存在するので、

| mb=λna ⇔ | n m | = | b λa |
すなわち、n:m=b:λaである。
| したがって、衝突回数は | b+λa GCF(b,λ) | −2となる。 |
問題はλ=1の場合であるから、b+a−2が解となる。
【応用】
発射角が60度の場合は、λ= となり、整数解が存在しないため、無限に衝突を繰り返すことになる。
となり、整数解が存在しないため、無限に衝突を繰り返すことになる。