◆HATさんからの解答。
まず、全ての誕生日の組合せを求める。
出席番号01の生徒の誕生日365通り
出席番号02の生徒の誕生日365通り
出席番号03の生徒の誕生日365通り
・
・
・
出席番号40の生徒の誕生日365通り
これらを掛けて、
全ての誕生日の組合せ 36540 通り ... a)
次に、誕生日が「同じでない」組合せを求める。
出席番号01の生徒の誕生日365通り
出席番号02の生徒が01と同じでないのは
(365−1)通り
出席番号03の生徒が01や02と同じでないのは
(365−2)通り
・
・
・
出席番号40の生徒が他と同じでないのは
(365−39)通り
これらを掛け合わせて、
誕生日が「同じでない」組合せは
| 365! (365−40)! | 通り ... b) |
a), b) より、 誕生日が「同じでない」確率は
| 365! 36540×(365−40)! |
従って、誕生日が「少なくとも同じ」確率
| 1− | 365! 36540×(365−40)! |
| =1− | 3.4×10101 3.1×10102 |
| =0.89 |
(エ)ですね。
丸め誤差はたぶん影響していないと思いますが... そこまでは検証していません。
【コメント】
この結果は、結構意外に感じた人も多かったのではないでしょうか。
実はクラス担任をしていると、ほとんどのクラスに誕生日の同じ生徒がいることを経験します。
確率が約90%。
この結果を見ると納得できますね。
◆広島県 清川 育男さんからの解答。
ペアになる組み合わせは、
| 39×40 2 | =780 |
| 1 365 |
| 1− | 1 365 | = | 364 365 |
| ( | 364 365 | ) | 780 |
したがって少なくとも1組でも誕生日が同じになる確率は、
| 1−( | 364 365 | ) | 780 | です。 |
【コメント】
これは非常にすっきりした解答ですね。
Windowsの電卓で計算したら 0.882・・・でした。
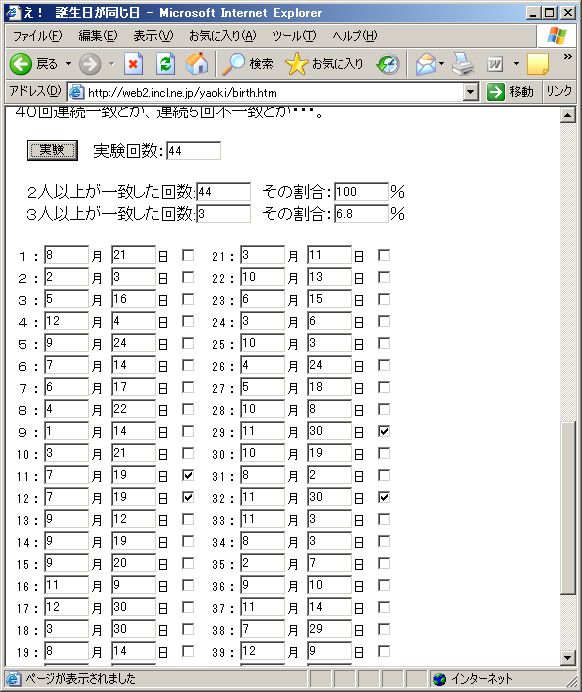
余談ですが、このページのソフトで実験したら、30回連続で「同じ誕生日の人」がいたことがありました。
90%近いというのが実感できますね。
もっとすごい記録が出た人がいたら教えてくださいね。
【東京都 ヨーゼフさんからのコメント】
清川氏の解答は、すっきりしていますが、間違いではないかと思います。
例えば3人のクラスの場合、氏によると、3人とも異なった誕生日になる確率は
| ( | 364 365 | ) | 3 | ・・(a) |
ところが、もしこの3人をA、B、Cとすると、
| 364 365 | × | 364 365 | × | 363 364 | × | ・・(b) |
(1)A、Bの誕生日が異なる確率
| 364 365 |
(2)B、Cの誕生日が異なる確率
| 364 365 |
(3)A、BおよびB、Cの誕生日が異なるという条件下で、C、Aの誕生日が異なる確率
| 363 364 |
したがって、3人とも異なった誕生日になる確率は
| 364 365 | × | 364 365 | × | 363 364 | × | ・・(b) |
数値計算して見ると、(a)、(b)は微妙に異なります。
クラスの人数が増えるとその差は次第に拡大しますが、35人でも1%位です。
◆大阪府の大学生 ふるふる さんからの解答。
40人のクラスで求める確率は、
1−(全員が違う誕生日の確率)
(全員が違う誕生日の確率)
| = | 365 365 | × | 364 365 | × | 363 365 | ・・・ |
| = | 365! 36540×(365−40)! |
よって求める確率
| =1− | 365! 36540×(365−40)! |
◆大阪府 ドラキュラ さんからの解答。
答え (エ)
1 - 364! ÷ (364 - 40 + 1)! ÷36539
◆東京都 ヨーゼフさんからの解答。
やや腕力になりますが、誕生日が一致する確率の側から計算してみました。
| 2人のクラスでは、一致する確率は、 | 1 365 |
| 2人の場合+ | 364 365 |
× | 2 365 |
n人のクラスでは、
| n-1人の場合+ | 364 365 | × | 363 365 |
×・・× | 367-n 365 |
× | n-1 365 |
数値計算は、最後の部分だけ補正して積算していけばよいので、見た目ほど大変ではありません。
40人のクラスでは、0.891になりました。
◆埼玉県 knog さんからの解答。
まず、クラスの中で一人も同じ誕生日の人がいない確率を考えてみます。
Aさんの誕生日が任意の1日だとすると、
| BさんがAさんと同じ誕生日でない確率は | 364 365 |
CさんがAさんともBさんとも同じ誕生日でない確率は、
| 363 365 | 、・・・となります。 |
したがって、40人全員が違う誕生日である確率は、
| 365 365 | × | 364 365 |
× | 363 365 |
×・・× | 326 365 |
(40人目)=約11% |
逆をいえば約89%の確率で、誰かが同じ誕生日であることになります。
意外に高い確率ですね。
◆東京都 むらやま さんからの解答。
40人のうち誕生日が同じ人が1組以上いる確率は,「一組もいない」確率の裏返しです.
一組もいない確率は
| 365 365 | × | 364 365 | × | 363 365 |
×・・× | 326 365 |
となり |
| 365P40 36540 | で計算できます. |
◆東京都 葛衣 奥人 さんからの解答。
まず、40人の誕生日の組み合わせは
36540通り。・・・(1)
で、「全員誕生日が異なる組み合わせ」は
365P40 通り。・・・(2)
(2)÷(1)を Excel を使って計算してみましたが、約11%になります。
残る約89%が、「誕生日が同じ人がいる確率」になるかと思います。
結構いるんですね。
同じクラスではありませんが、親戚で「干支も誕生日も同じ人」がいますよ。
ちょうど48離れています。
◆宮城県 アンパンマン さんからの解答。
【追加問題】
P(同じ誕生日3人以上いる) =1-P(同じ誕生日の人がいない)−P(同じ誕生日の二人、1組いる)-P(同じ誕生日の二人、2組いる)-P(同じ誕生日の二人、3組いる)-...-P(同じ誕生日の二人、[m/2]組いる)m人の生徒がいるとします。
P(同じ誕生日の人がいない)
=P(同じ誕生日の二人、0組いる)
| = | 365Pm 365m |
P(同じ誕生日の二人、i組いる(同じ誕生日の3人以上はない))
| = | 365Pm-i | m!
(m-2i)!(2!)i i! | /365m |
P(同じ誕生日3人以上いる)
| =1- | [m/2] Σ i=0 |
365Pm-i | m!
(m-2i)!(2!)i i! | /365m |
m=40の場合、P(同じ誕生日3人以上いる)=0.066889
つまりだいたい6.69%です。
◆福岡県の中学校3年生 ヒロ さんからの解答。
単刀直入に言うと答えは(エ)となります。
まず40人とも誕生日が違っている確率を計算します。
たとえば出席番号順にでも考えていって、最初の人はどの日が誕生日でもよい、
二番目の人は〈365−1)通りある、
三番目の人は(365−2)通りある・・
そして四十番目の人は(365−39)通りあると下のように計算します。
| 364 365 | × | 363 365 |
×・・× | 326 365 |
≒0.109 |
◆40回以上連続不一致の結果を送っていただきました。

◆匿名 さんからの解答。
40人のクラスで3人以上が同じ誕生日の確率は、
1-{(全員バラバラの確率)+(2人だけ同じ確率)}
| 全員バラバラの確率= | 365P40 36540 |
| 2人だけ同じ確率= | 40C2×365P39 36540 |
| よって、3人以上が同じ確率=1-{ | 365P40 36540 |
+ | 40C2×365P39 36540 |
} |