◆愛知県 Y.M.Ojisan さんからの解答。
【2個の場合】
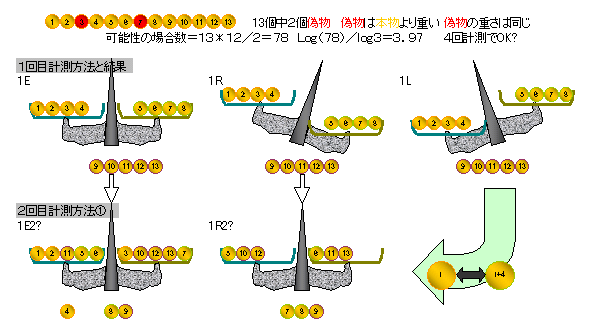
2個以上になると、偽物の事前情報にもいろいろのケースが考えられるが、ここでは偽物は同じ重さで、本物より重いとする。
| すると、 3n-1< | A(A−1) 2 |
≦3n |
一般的には解けなかったが、クリティカルな場合として、
A=13 と 22の場合に
| A=13: | log(13*12/2) log(3) |
=3.97 →4回 |
| A=22: | log(22*21/2) log(3) |
=4.95 →5回 |
で予測式どおりの回数で偽物の2個を見つける方法があった。
下図に方法を示す。

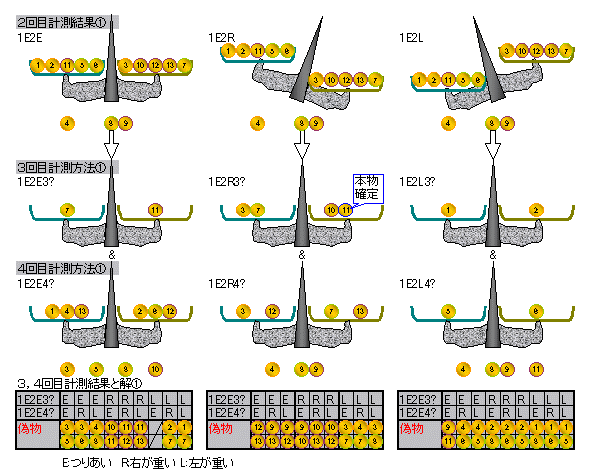
さらに、1E2? の場合は下図を実施し、全4回で偽物が分かる。
なお、図中で番号がなくなっているコインは本物であることが確定しているものである。
(11番除く)
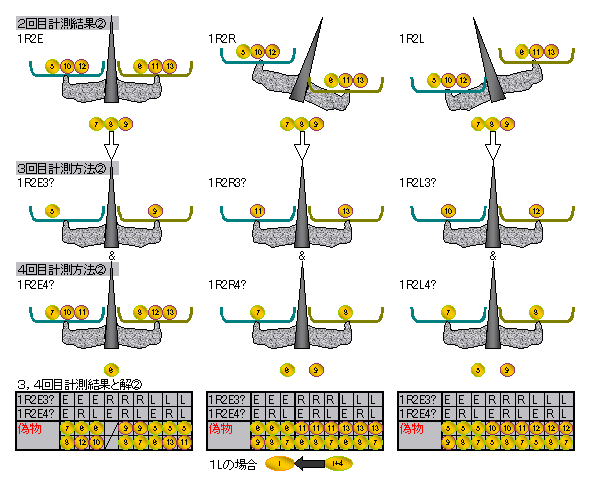
一方、1R2? の場合は下図を実施し、やはり全4回で偽物が分かる。
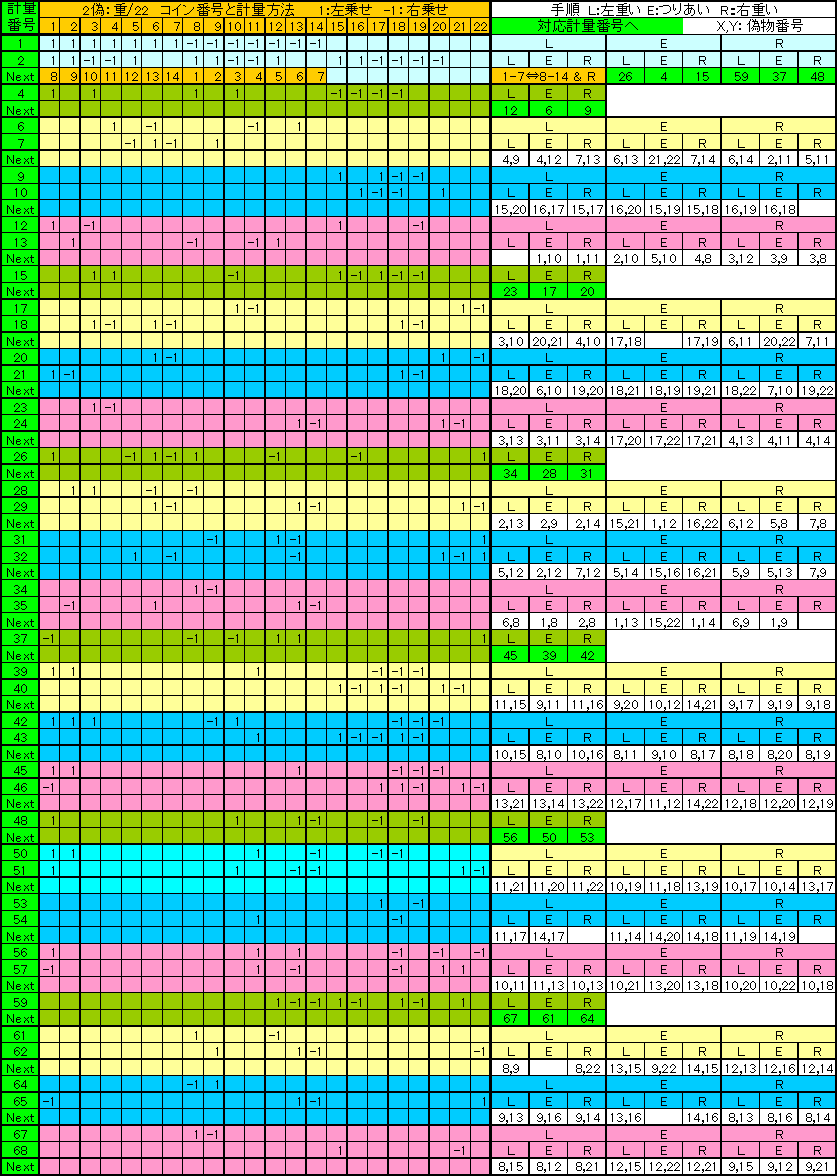
【A=22の場合】
最初は7個ずつ計る(計量番号1番).
以下下表に従い全5回で2個の偽物が見つけられる。
2回目は軽量番号2番を常に実施。の結果
たとえば 1番でつりあい:E 2番で右が重い:R場合は
E-Rの欄をみて、3回目の計量は計量番号15を実施する。
さらにその結果(L,E,R)により、4回目と5回目の計量を計量番号23,24 または17,18 または20,21 で実施する。
その結果たとえば 23,24番結果がLLなら、3と13が偽ものである。
なお、1回目の結果がLの場合は1〜7と8〜14交換して下表を用いる。