�����m���@Y.M.Ojisan ����̉�
�y���P�z
�\�z�͐������B
��@�����Qt�|�P�@�@t���R�ɂ�����
2m�bm-1�߂R�@mod �W�ł���B�\�\�\�\�i�P�j
����@2m�bm-1�@���W�@�ł��邩��
2m�bm-1���Qk�|�P�߂V�@mod �W�@�ł���R�ɂ͂Ȃ�Ȃ��B
�i�P�j�̏ؖ�
�����Qt�|�P�ɂ����Ă̂�2m�bm-1�͊�ł���B
�]���āA2m�bm-1�@mod �Q3�@���l����Ƃ���
�P�`�Q���̐��́@�f�������̊����mod �Q3�̂ݍl������悢�B
���āA�P�`�Qp�@���̂Q0�~��̂��̂Ɋւ��Ă�mod �W��
�P�A�R�A�T�A�V�A�P�A�R�A�T�A�V�B�B�B�B�B�P�A�R�A�T�A�V
�ƂS���̌J��Ԃ��ł���B
�Ƃ���Ł@�P�~�R�~�T�~�V�߂P�@mod�@�W�ł��邩��
�����̐ς��߂P�@mod�@�W�ł���B
����͂P�`�Qp�@���́@�Qp�3�~��@�̂��̂܂œ����ł���B
�Qp-2�~��̂��̂Ɋւ��Ċ����mod �W�́@�P�A�R�̂Q���ł���B
�Qp-1�~��̂��̂Ɋւ��Ċ����mod �W�́@�P�݂̂ł���B
�Qp�~�P�̂��̂Ɋւ��Ă̊����mod �W�́@�P�݂̂ł���B
�]���ā@�����Q�ɂ����ā@
�o�i�Qp�j�I�̊�������p�߂R�@mod�@�W�@�ł���B�@�\�\�\(�Q)
| 2m�bm-1�� | (�Qt+1�|�Q)�I (�Qt�|�Q)�I�Qt�I |
�� | �Qt+1�I �Qt�I�Qt�I |
�~ | �Qt(�Qt�|�P) �Qt+1(�Qt+1�|�P) |
�ƍP���ό`�ł���B
�Q�̔{�����������ā@mod�@8���l����� �����R�̂Ƃ� �i�Q�j��K�p����ƁA
| 2m�bm-1�� | 3 3�~3 |
�~ | 1�~7 1�~7 |
�߂R�@mod�@�W |
�ł���B���݂ɂ����Q�̂Ƃ�
| 2m�bm-1�� | 3 3�~3 |
�~ | 1�~3 1�~7 |
�߂V�@mod�@�W |
�ł���B
�y���z�z
�u�f�[�^���k�����̍\���Ɋւ��錤���v�Ƃ��āA���p�ƌ��т��Ƃ������ƂłƂĂ������[���v���܂����B
����錧�@����ɂ��� ����̉�
����m��2t-1�̂Ƃ�2mCm-1�͋����ƂȂ邱�Ƃ������܂��B
���R�A2mCm-1�͊�ł���2k-1�ɂ͂Ȃ肦�܂���B
�y�z
�y���P�z
| n!�̑f�������������Ƃ���p�̎w���� | �� i=1 |
[ | n pi |
]�ƂȂ�B |
�y�ؖ��z
n!�̎w����
| �� i=1 |
{i*(pi�Ŋ�����pi+1�Ŋ����Ȃ�1�ȏ�n�ȉ��̎��R���̌�)} |
| = | �� i=1 |
{i*([ | n pi |
]-[ | n pi+1 |
])} |
| = | �� i=1 |
{(i-(i-1))*[ | n pi |
]} |
| = | �� i=1 |
[ | n pi |
] |
�ؖ��I
�y���Q�z
���A���������Ƃ����[��+��]-([��]+[��])=0,1�ƂȂ�B
�y�ؖ��z
���ƃ��́A0����,��1�Ȃ�������ƃ�p���āA
��=[��]+���A��=[��]+�Ə�����B
��+��=[��]+[��]+��+�A0����+��2���
0����+��1�̂Ƃ�[��+��]=[��]+[��]�A
1����+��2�̂Ƃ�[��+��]=[��]+[��]+1
�����[��+��]-([��]+[��])=0���邢��1�ƂȂ�B
�ؖ��I
�y���R�z
���R��N��s�i�@�ŕ\��(�������s��2�ȏ�̎��R��)�B
| N= | �� i=0 |
(ai*si)�ƂȂ�܂��B |
| ���̂Ƃ��Aah��ah= | [ | N sh |
]-s[ | N sh+1 |
] |
�y�ؖ��z
| N sh | ={ | h-1 �� i=0 |
(ai*si)}/sh+{ | �� i=h |
(ai*si)}/sh |
| 0�� | h-1 �� i=0 |
(ai*si)�� | h-1 �� i=0 |
{(s-1)*si}=(s-1)* | sh-1 s-1 |
=sh-1��sh��� |
| [ | N sh | ]= | h �� i=h |
(ai*si-h) | =ah+ | �� i=h+1 |
(ai*si-h) |
| ���l��[ | N sh+1 | ]= | �� i=h+1 |
(ai*si-h-1) |
| s*[ | N sh+1 | ]= | �� i=h+1 |
(ai*si-h) |
| �����a | h | =[ | N sh |
]-s[ | N sh+1 |
]�ƂȂ�B |
�ؖ��I
�y���S�z
n��r��0��r��n�Ȃ鎩�R���Ƃ���B
n��r��p�i�@�ŕ\���B
| n= | �� i=0 |
(bi*pi)�Ar= | �� i=0 |
(ci*si)�An-r= | �� i=0 |
(di*si)�A |
����0�ȏ�̐���h�ɑ���bh��ch+dh �ƂȂ�Ƃ��A
nCr��p�Ŋ�����B
�y�ؖ��z
���R���
| b | h | =[ | n ph |
]-p[ | n ph+1 |
]�Ac | h | =[ | r ph |
]-p[ | r ph+1 |
]�Ad | h | =[ | n-r ph |
]-p[ | n-r ph+1 |
] |
���̏���bh��ch+dh�ɑ�������
| [ | n ph | ]-p[ | n ph+1 |
]��([ | r ph |
]-p[ | r ph+1 |
])+([ | n-r ph |
]-p[ | n-r ph+1 |
]) |
| [ | n ph | ]-[ | r ph |
]-[ | n-r ph |
]��p([ | n ph+1 |
]-[ | r ph+1 |
]-[ | n-r ph+1 |
]) |
������Q���
| [ | n ph+1 |
]-[ | r ph+1 |
]-[ | n-r ph+1 |
]=0���邢��1�ł���B |
| [ | n ph+1 |
]-[ | r ph+1 |
]-[ | n-r ph+1 |
]=0�Ɖ��肷��� |
| [ | n ph |
]-[ | r ph |
]-[ | n-r ph |
]��0�ƂȂ�B |
����͕��Q��
| [ | n ph |
]-[ | r ph |
]-[ | n-r ph |
]=0���邢��1�ɔ�����B |
| �����[ | n ph+1 |
]-[ | r ph+1 |
]-[ | n-r ph+1 |
]=1�ł���B |
| nCr= | n! r!(n-r)! |
��f�������������Ƃ���p�̎w���͕��1��� |
| �� i=1 |
([ | n pi |
]-[ | r pi |
]-[ | n-r pi |
]) |
| ���Q���[ | n pi |
]-[ | r pi |
]-[ | n-r pi |
]=0���邢��1������ |
| �� i=1 |
([ | n pi |
]-[ | r pi |
]-[ | n-r pi |
])��[ | n ph+1 |
]-[ | r ph+1 |
]-[ | n-r ph+1 |
]=1 |
�����nCr��p�Ŋ����邱�Ƃ��킩��B
�ؖ��I
���āA�`����m��2t-1�̂Ƃ��A2mCm-1�͋����ƂȂ邱�Ƃ�����
m�������̂Ƃ��Am-1��m+1�͊�ł���B
2m��2�i���ŏ�����20�̌���0�Am-1�Am+1��20�̌���1
����ĕ��S���2mCm-1�͋����ł���B
m����̂Ƃ��Am�̈�ԉ��̌���1�ł���B
����āAm-1��20�̌��ȊO�̌���m��20�̌��ȊO�̌��͈�v����B
������m��2t-1�ł��邱�Ƃ��v���o�����B
����āAm��2�i���ŕ\���B
| m= | �� i=0 |
(ei*2i) |
����ƁAeh-1=0�Aeh=1�ƂȂ鎩�R��h�����݂���B
| 2m= | �� i=0 |
(ei*2i+1)= | �� i=1 |
(ei-1*2i) |
| m-1= | �� i=1 |
(ei*2i) |
m+1��2�i���ŕ\����
| m+1= | �� i=1 |
(fi*2i) |
2m,m+1,m-1��2h�̌��͂��ꂼ��A0,fh,1
����āAfh�̒l��0�ł��낤��1�ł��낤���A
0=eh-1��1+fh=eh+fh����������B
����āA���S���2mCm-1�͋����ł��邱�Ƃ������ꂽ�B
�I
�y�R�����g�z
Y.M.Ojisan ����̉Ƃ��킹�āA
2mCm-1=2k-1�ƂȂ�̂�
m=1���邢��m=3�̏ꍇ�Ɍ����邱�Ƃ�������܂��B
����āA�Ђ�������̗\�z�͐��������Ƃ�������܂����B
�������s�@�ۂ��� ����̉�
Y.M.Ojisan ����� mod 8 �ōl���������ȏؖ������Ă��邤���ɁC�i�P�j�̕ʏ��v�����܂����B
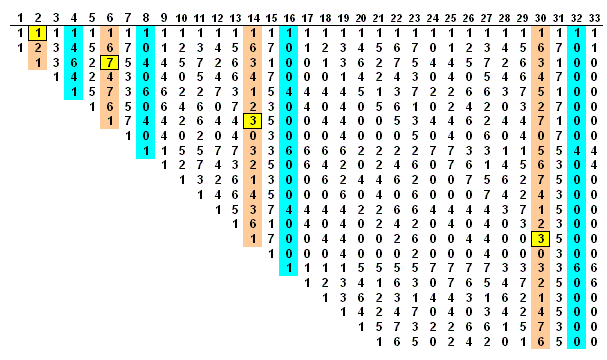
Pascal �̎O�p�`�� mod 8 �ōl����ƁC2N �̒i�i���}�̐F�j�͂��ꂢ�Ȍ`�����Ă��܂��B
N��2 �̂Ƃ��ɂ́C1, 4, 6, 4, 1 �̊Ԃ� 2N-2 - 1 �� 0 ���������`�ɂȂ�̂ł��B
���̏ؖ��͊ȒP�ł����C���Ƃ��Ε�����g�������͉̂��L�́y���z�̂悤�ɂȂ�܂��B

���� m = 2t-1 �̒i�i�s���N�F�j�̒����t�߂́Cm = 2t �̒i�̒����t�߂̒l����v�Z�ł��܂��F
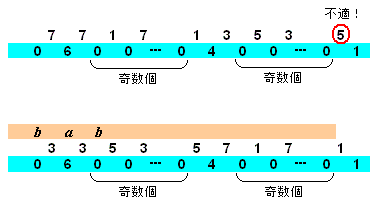
m = 2t �̒����� 6 �ɑ��āC6 �����ޒ���̍s������ 2 �̍��͓���������C���� 3 ���C���� 7 �ƂȂ邵������܂���B
�������C7 �̏ꍇ�͏�}�̂悤�ɉE�[�� 1 �ɂȂ�Ȃ��̂œK���܂���B
�����Œ����� 2 ���� 3 �ƌ��܂�C���̏�̍s�ł� a+b��3 (mod 8) �ƂȂ�܂��B
������ t��3 �̂Ƃ��ɂ� a��0 �ƂȂ邱�Ƃ����̂悤�ɏؖ��ł���̂ŁCb��3 �ƂȂ�킯�ł��B
���ہCm = 2n-1 (�) �̂Ƃ��C2mCm ��
| (4n-2)(4n-3)�c(2n) (2n-1)(2n-2)�c1 |
= | (�)�~2n (n-1)! |
�����ŁC����� (n-1)! �Ɋ܂܂�� 2 �̍ő�w����
| [ | n-1 2 |
] + [ | n-1 4 |
] + [ | n-1 8 |
] + [ | n-1 16 |
] + �c |
(2t-2-1) +(2t-3-1)+ �c +(21-1)
= 2t-1 - t
= n - t
�ƂȂ�܂��B
���������āCm = 2t-1 �̂Ƃ��C2mCm �Ɋ܂܂�� 2 �̍ő�w����
n - (n - t) = t �ƂȂ�C
t��3 �̂Ƃ� 2mCm �� 0 (mod 8) �ƂȂ邱�Ƃ��킩��܂��B
�y���z
2 �̓��������̐����W��������
f(x) = ��ak xk�Cg(x) = ��bk xk �̌W���̊Ԃ�
ak �� bk (mod n) �̊W������Ƃ��C
f(x) �� g(x) (mod n) �ƒ�`����B
���̂Ƃ��Cmod 8 ��
(1+x)4 = 1 + 4x + 6x2 + 4x3 + x4
(1+x)8
�� (1 + 4x + 6x2 + 4x3 + x4)2
�� 1 + 4x2 + 6x4 + 4x6 + x8
�� (1+x2)4
�ł��邱�Ƃɒ��ӂ���ƁC
(1+x)16
�� {(1+x2)4}2
�� (1+x2)8
�� (1+x4)4
(1+x)32
�� {(1+x4)4}2
�� (1+x4)8
�� (1+x8)4
�c
�ȂǂƂȂ�B
�y���z�z
�F�̍s�̂悤�Ȕ����������͗L���łȂ������悤�Ɏv���܂��B
���߂ċC�Â��܂����B
�������s�@�ۂ��� ����̉�
Pascal �̎O�p�`�ɂ��ؖ������܂��������̂ɋC��ǂ����āC
2mCm-1 ����@�́@m = 2t-1 (t = 1, 2, �c)
�ɂ��Ă��l���Ă݂܂����B
�Ă� mod 8 �� Pascal �̎O�p�`�����ƁC
2N �̒i�� 1�C4�C6�C4�C1 ���Ԃ� 2N-2-1 ��0 ������ŕ���ł��܂��B
(��L�̒��Q��)
���̂Ƃ��CPascal �̎O�p�`�̐�������C���炩��
0��n��2N �̂Ƃ��C
C(2N + n, r) �� ���� (n��r��2N)
C(2N + n, r) �� � (r = n, 2N)
�ł��邱�Ƃ��킩��܂��B
(���ŏ��������C���}�̗� (N=4) ������Έ�ڗđR�ł���)
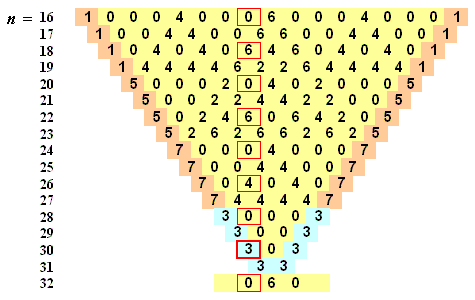
����ɁCn �͈̔͂� 4 �ɕ����āC
0 ��n��1�E2N-2 �̂Ƃ��C
�@C(2N + n, r) �� 1 (r = n, 2N)
1�E2N-2��n��2�E2N-2 �̂Ƃ��C
�@C(2N + n, r) �� 5 (r = n, 2N)
2�E2N-2��n��3�E2N-2 �̂Ƃ��C
�@C(2N + n, r) �� 7 (r = n, 2N)
3�E2N-2��n��4�E2N-2 �̂Ƃ��C
�@C(2N + n, r) �� 3 (r = n, 2N)
�ɒ��ӂ���C�܂Ƃ߂đS���ؖ��ł��Ă��܂��܂����B