より、ｍ＝２−
、ｎ＝２＋と置く。（逆でも結果は同じ）◆静岡県 ヨッシー さんからの解答。
２×３ の敷き方は、問題の通り３通りです。
左から、Ａ，Ｂ，Ｃ とします。
このとき、一番下の３マスに注目すると、
「縦縦縦」「横縦」「縦横」が１通りずつです。
これを（１，１，１）と書きます。
これらの下に、Ａ，Ｂ，Ｃをつなげて、４×３ にするとします。
その組み合わせは、３×３＝９ 通り。
さらに、「横縦」の下にＢが来た場合、継ぎ目に出来る横横の正方形を縦縦に変えることが出来ます。
「縦横」の下にＣが来た場合も同じです。
つまり、（３，４，４）の１１通り出来ます。
６×３では、
(１１，１１＋４，１１＋４)＝(１１，１５，１５)の４１通り。
８×３では、
(４１，４１＋１５，４１＋１５)＝(４１，５６，５６)の１５３通り。
１０×３では、
(１５３，１５３＋５６，１５３＋５６)＝(１５３，２０９，２０９)の５７１通り。
これをまとめると、
２ｎ×３の状態（Ｘn，Ｙn，Ｙn）に対して、
２（ｎ＋１）×３は（Ｘn＋２Ｙn，Ｘn＋３Ｙn，Ｘn＋３Ｙn） となります。
ａn＝Ｘn＋２Ｙn とすると、
ａn+2＝４ａn+1−ａn
ａ1＝３、ａ2＝１１ となります。
【問題１】 １１通り
【問題２】 ４１通り
【問題４】 １５３通り、５７１通り
【問題３】は、どんな形に持っていけばいいかわかりませんでした。
【コメント】
いつもながら鮮やかな解答ですね。
隣接３項間の関係がでているので、問題３は必要ないかもしれません。
どなたか一般項を計算してみませんか。
◆静岡県 ヨッシー さんからの解答。
ａn+2＝４ａn+1−ａn
ａ1＝３、ａ2＝１１ の一般項です。
ａn+2＝４ａn+1−ａn が
ａn+2−ｍａn+1＝ｎ（ａn+1−ｍａn）と置けたとします。
このとき、ｍ＋ｎ＝４、ｍｎ＝１より、ｍ、ｎは、
ｘ2−４ｘ＋１＝０の解。
ｘ＝２±より、
ｍ＝２−、ｎ＝２＋と置く。（逆でも結果は同じ）
ａn+2−(２−)ａn+1＝(２＋)｛ａn+1−(２−)ａn｝
ｂn＝ａn+1−(２−)ａn とおくと、
ｂn は初項 ｂ1＝１１−(２−)×３＝５＋３
公比 ２＋の等比数列。よって、
ｂn＝ａn+1−(２−)ａn＝(５＋３)(２＋)n-1
移項して
ａn+1＝(２−)ａn＋(５＋３)(２＋)n-1
これが、
ａn+1＋(２＋)ｐ＝(２−)(ａn＋ｐ)と置けたとします。
このとき
−２ｐ＝(５＋３)(２＋)n-1 より
| ｐ＝− | ９＋５ ―――――― ６ | × | （２＋）n-1 |
よって
| ｃn＝ａn− | ９＋５ ―――――― ６ | × | （２＋）n-1 |
ｃn+1＝（２−）ｃn
ｃ1＝（９−５）／６ より、
ｃnは、初項（９−５）／６、公比（２−） の等比数列。
ｃn
| ＝ａn− | ９＋５ ―――――― ６ | × | （２＋）n-1 |
| ＝ | ９−５ ―――――― ６ | × | （２−）n-1 |
以上より ａnの一般項は
| ａn＝ | ９−５ ―――――― ６ | × | (２−)n-1 | ＋ | ９＋５ ―――――― ６ | ×(２＋)n-1 |
これで、ｎが自然数の時、ａn が整数になるから不思議です。
【コメント】
私も昔、フィボナッチ数列の一般項を見て、整数になるわけはないと思ったのですが、いざ計算してみると見事にルートが消えていき、感心した記憶があります。
◆東京都 GOYAさんからの解答。
【質問１】
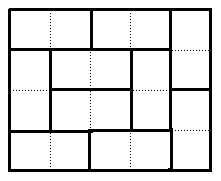
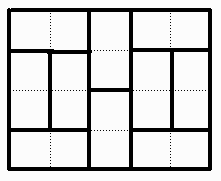
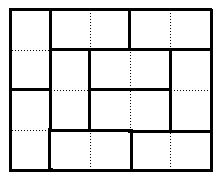
の３種類。
【質問２】
４．５畳、１２．５畳のような正方形の間であれば半畳の畳は中央と４隅の合計５カ所に置けます。
これは畳を渦巻き上に外側から内側または内から外に於いていく方法で、半畳の畳を最初または最後に敷けばルールを守って敷くことができることで説明できます。
渦巻き状以外の敷き方でルールを守って敷く方法があれば他にも置ける場所があるかもしれませんが、１７．５畳より狭い間では不可能なようです。
正方形でない間の場合は上記の５箇所ではありません。
渦巻き畳に敷いていくと４隅には置けますが中央には置けないようです。
代わりに別の場所に置けます。
例えば１．５畳×２．５畳の７．５畳では、敷き方は渦巻き状の他に１．５×１．５の４．５畳と１．５×１の３畳に分けて各々を渦巻き畳に敷く方法があります。
これにさらに１．５×１の３畳を追加した１０．５畳を考えると、この３畳は４．５＋３＋３の形にも３＋４．５＋３の形にも追加できるし、４．５＋６という敷き方もできる．．と考えていくと半畳の畳を置ける位置を特定するのは困難なように思います。