『Ｎ枚のカード』解答

◆宮城県　斉藤　誠さんからの解答。

直感的に予想すると、１〜Ｎから何回か選んだときにその和がＮを越えるかどうかを考える。
分布は１〜Ｎまでの一様分布である。
１回では高々Ｎであるので２回以上選ばなければならない。
２回とすると５０％の確率で中位数より上か下が選ばれる。

中位数以下の平均はＮの

１ ４

中位数以上の平均はＮの

３ ４

合計でＮ。

もう一枚選らばなければなれないので３回必要。

ただし、中位数以上を２回選ぶ確率もあるので２回〜３回が答えの範囲か。

１を連続で選ぶ可能性もあるので最高Ｎ＋１もあり得るが確率は低い。
そこでこれら、Ｘ回の総和がＮを越える確率の平均を求める必要がありそうだ。

Ｎの小さい順に調査する。
Ｎ＝１の場合
　常に２回・・・１回では高々１なので自明

Ｎ＝２の場合
　最高３回（１を３回）なので組み合わせを考える。

　　　１１
　　　１２
　　　２１
　　　２２

「１１」の組み合わせ以外はＮを越えるので
　　３回が一通り、２回が３通り

平均は　Ｘ＝（３×１＋２×３）÷４（通り）＝９÷４＝２．２５

Ｎ＝３の場合 　最高４回（１を４回）なのでＮ＝２と同じく組み合わせを考える。

１１１ １２１ １３１
１１２ １２２ １３２ 
１１３ １２３ １３３ 

２１１ ２２１ ２３１ 
２１２ ２２２ ２３２ 
２１３ ２２３ ２３３ 

３１１ ３２１ ３３１ 
３１２ ３２２ ３３２ 
３１３ ３２３ ３３３

　４回　　１通り
　３回　　８通り
　２回　１８通り

よって

　平均　Ｘ
＝（１×４＋３×８＋２×１８）÷２７
＝６４÷２７
＝約２．３７０

Ｎ＝４の場合は
　組み合わせが多いので調査結果のみ記述すると

　５回　　　１通り
　４回　　１５通り
　３回　　８０通り
　２回　１６０通り

で全組み合わせは２５６通り

よって 　平均　Ｘ
＝（１×５＋２×１５＋３×８０＋２×１６０）÷２５６
＝６２５÷２５６
＝約２．４４１

Ｎ＝５、６・・・・の場合は、考えたくない。
コンピュータにお願いしたい。

ここまでを整理し、一般の場合を予想すると

Ｎ＝２の時の期待値　Ｘ＝

９ ４

＝

３2 ２2

Ｎ＝３の時の期待値　Ｘ＝

６４ ２７

＝

４3 ３3

Ｎ＝４の時の期待値　Ｘ＝

６２５ ２５６

＝

５4 ４4

ここで分母、分子に規則性がありそうなので、一般には

となりそうです。

また、極限値は

となるのでないでしょうか。

「期待値」なる概念がいまいち理解不足で、極限値ｅを頼りにあわせ込んだきらいがありますが。
確率、統計は難しい。

今日の降水確率は５０％です・・・降るのか降らないのかどっち。
「２回の予想のうち１回は当たる。」？？？

◆石川県　Takashiさんからの解答。

カードをx回引いたときの数字の順列の個数をＧ（x）、
数字の合計がｎ以下となる順列の個数をＦ（x）、
カードをx回引いたときの合計がｎを超えている確率をＱ（x）、
x回目に初めて合計がｎを超える確率をＰ（x）とすると、

Ｇ（x）＝ｎ^x

Ｑ（x）＝１−

Ｆ（x） Ｇ（x）

Ｐ（１）＝０、
Ｐ（x）＝Ｑ（x）−Ｑ（x-1）　【x＞１】

下図の様にｎ個のボールの間か右端にx本の線を入れた時、各線で区切られたボールの数を各回のカードの数字に見立てると、このような線の入れ方の組み合わせの個数がＦ（x）と等しくなる事がわかる。

Ｆ（x）＝_nＣ_x

これらを計算すると、

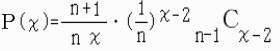
よって、xの期待値 Ｍ（ｎ） は、

Ｍ（ｎ）＝

n+1 Σ x=2

xＰ（x）

計算すると、

Ｍ（ｎ）＝（１＋

１ ｎ

）

n

≪図≫

  　　　１　　　　　２　　　３　　　　・　・　・　 x-1 　　　　　　　　x
  ○　○┃○　○　○┃○　○┃○　○　・　・　・　○┃○　○　○　○　○┃
  １　２　３　４　５　６　７　８　９　・　・　・　　　　　　 ｎ-2 ｎ-1 ｎ

計算の部分は、やや不安があります。間違っているかも ?!

◆大阪府の高校生　Taka　さんからの解答。

m≦ｎ　の時　

X₁＋X₂＋X₃＋・・・・X_ｍ＝ｎ

を満たす、自然数の組（X₁、X₂、・・・X_ｍ）を考える。

これは、_mＨ_m-n=_n-1C_n-m=_n-1C_m-1・・(1)

求める確率は、
（ｋ回以上かかる確率）−（ｋ＋１回以上かかる確率）である。

まずK回以上かかる確率は、(1)を考えて

(

n-1Ck-1 n

)

k-1

・・(2)

そして、(

n-1Ck n

)

k

・・(3)

Ｐ_k=(2)−(3)とおく。

Ｅ_ｎ
＝Σk×Ｐ_k

＝Σ[{（k-1）(

n-1Ck-1 n

)

k-1

−ｋ×(

n-1Ck n

)

k

}＋(

n-1Ck-1 n

)

k-1

]

_n-1Ｃ_n＝０を利用して

Ｅｎ＝Σ

(

1 n

)

k-1

×n-1Ｃk-1

二項定理を逆に使い、

Ｅｎ＝

(１＋

1 n

)

n-1

＝

(１＋

1 n

)

n

×(１＋

1 n

)

-1

　→ｅ （ｎ→∞）

◆東京都　Toshi さんからの解答。

今、何枚か取り出した結果の合計値がkである場合、
次にnを超えるまでに取り出す枚数の期待値をE(k)とします。
（k=0,1,…,n）

すると、E(k)には次の関係式が成り立ちます。

E(k)=1+

1 n

*(E(k+1)+…+E(n)) (k=0,1,…,n-1)

E(n)=1

この式の考え方は、例えばk=n-1の場合を考えると、次に2以上を引く場合は、この1枚をひいた時点でnを超える。

よって、確率(1-

1 n

)で必要枚数の期待値は1。

次に1を引く場合は、この1枚だけではまだnを超えず、あとE(n)枚が必要です。

よって、確率

1 n

で、必要枚数の期待値は(1+E(n))。

よって、E(n-1)=(1-

1 n

)*1+

1 n

*(1+E(n))=1+

1 n

*E(n)。

一般のkについても同様の考え方です。
（数学的には条件付期待値の概念をつかっているわけですね。
E(E(X|Y))=E(X)で、今の場合、Yを次に引くカードとしているわけです。）

上の漸化式から、

E(k)=(1+

1 n

)*E(k+1) (k=0,1,…,n-1)

が簡単に導けますから、結局、

E(0)=(1+

1 n

)

n

*E(n)=(1+

1 n

)

n

となります。

【感想】

条件付期待値の概念はわかりにくいですが、こういう問題だと感覚的に理解しやすいかもしれませんね。

　『Ｎ枚のカード』へ

　数学の部屋へもどる