
◆京都府 釜坂 正芳 さんからの解答。
【問題1】
[図1]のように,直角を夾む2辺をx,yとし,内接する正方形の1辺をzとする。

△APQ∽△PBRから,
AQ:PQ=PR:BR…(ア)
(x−z):z=z:(y−z) を解いて,
| z= |
xy ――――― x+y |
また,
| AQ=x−z= |
x2 ――――― x+y | >0 |
| BR=y−z= |
y2 ――――― x+y | >0 |
となり,直角三角形に内接する正方形がただ一つ存在する。
また,AP:PB=AQ:PR=x:yとなり,これらをまとめると,[図2]のようになる。
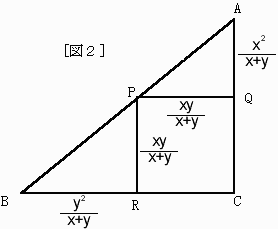
【問題2】
・三角形1の面積
式(ア)でAQ=a,BR=bとすると,
a:z=z:b
よって z2=ab
・三角形2の面積
| 正方形の1辺z= |
cd ――――― c+d | であるから, |
| 面積 z2= |
c2d2 ―――――― (c+d)2 |
・三角形3の面積
[図2]からx:y=e:fであるから,
x=ke,y=kfとすると
正方形の面積
| z2= |
(ke)2(kf)2 ―――――――― (ke+kf)2 |
| = |
k2e2f2 ―――――― (e+f)2 |
また,三平方の定理より,
k2e2+k2f2=(e+f)2であるから,
正方形の面積
| z2= |
e2f2 ―――――― e2+f2 |
【問題3】
a:b=c2:d2と[図2]から,三角形1と三角形2は相似であり,面積が等しいから,合同。
また,問題1から,内接正方形はユニークであるから,内接正方形の面積も等しい。
【問題4】
c:d=e:fと[図2]から,三角形2と三角形3は相似であり,斜辺が等しいから,合同。
また,問題1から,内接正方形はユニークであるから,内接正方形の面積も等しい。
【コメント】
直角三角形に内接する正方形は,高校入試はもちろん(内接円にくらべると少ないが),中学入試にも頻出の形なので,慣れ親しんでいましたが,恥ずかしながら,一般の場合を考えたことはありませんでした。
いい勉強になりました。
これまた頻出の形[図3]と同じになるんですね。

zはxとyの調和平均の半分になっています。
xオームとyオームの2つの抵抗の並列回路の合成抵抗zオームとも同じです。
もっとも,[図3]を台形にしてしまうと,2zが現れますから,調和平均そのものになります。
出版社は忘れましたが,教科書にもそれを証明させる問題が出ていたような…。
◆滋賀県 一平 さんからの解答。
【問題1】
下図のように、座標平面上に三角形をおく。
Pの座標は(a,b)とする。
ただし、a,b>0
また直線OPの方程式は,
| y= |
b ―― a | x |
今,三角形に内接する長方形RSTQにおいて
f(x)=SR−ST(ただしxはS及びTのx座標)とすると、
f(x)はxの連続関数で、
| f(x)=(a−x)− |
b ―― a | xとなる。 |
ここで,
f(a)=−b<0 ,f(0)=a>0より、中間値の定理を用いれば
f(c)=0となるcが存在し、この場所が、正方形を作る。
また、
| f'(x)=―1− |
b ―― a | <0で |

◆千葉県 ひのひの さんからの解答。
【問題1】
正方形の3頂点が直角三角形の直角をはさむ辺上にあるように内接するとき、残りの1点は直角三角形の直角の角二等分線上にのみ存在します。
そして、これと直角三角形の斜辺の交点が正方形を決める唯一の点です。

【感想】
中学生の皆さんには「示した」ことになるかも、ということで送りました。
角二等分線上にある理由は三角形の合同で説明できるし、平行でなく、重ならない2直線はただ1点で交わることは「一次関数」で勉強しましたし...
【出題者のコメント】
【問題1】
私の出題意図も3人目の方の考えと同じです。
つまり、
「考えている正方形がもし存在するなら、直角の二等分線が対角線になる。
実際に直角の二等分線を引くと、確かに斜辺とただ1点のみで交わる。
証明終わり」
ひょっとして、この証明ではあいまいなのでしょうか?
◆京都府 釜坂 正芳 さんからのコメント。
あまくはないと,思います。
十分証明になっていると思います。
問題1の解答としては,スマートだと思います。
私も,「問題1」しか,なかったら,意図どおりの証明をしたと思います。
(計算嫌いですから・・・)
問題2〜4を見て,問題1は単に予備証明だと思いましたし,どうせ計算するんだったら,・・と,実際に求めて,ユニークに存在することを証明したわけです。
労力の節約です。
元来ナマケモノですので・・・。