◆愛知県 Y.M.Ojisan さんからの解答。
【問題3<自然数の場合>の若干別解 と Z,Qの解】
問題4の方法を問題3に適用して見ました。
【定義】
Hp(n)=f(n*p3)3、n∈非負整数:N0 ,p∈自然数:N
【線形関係】
m、n、s、t∈N0
m3+n3= s3+t3 ならば Hp(m)+Hp(n)=Hp(s)+Hp(t)
∵ (mp3) 3+(np3)3= (sp3)3+(tp3)3 が成立するから。
【限定的線形関係】
n.∈N0,Hp(2n3)=8*Hp(n3)
∵ (n3)*p3 =(np) 3よりHp(n3) = f(pn)9
(2n3)*p3 =(np3) +(np3)よりHp(2n3) =8*f(n) 9
この2種の線形関係を用いて、前回同様に連立線形方程式を解くと、
N=624までの方程式からn≦130までのHp(n)を
Hp(1)とHp(3)で表すことが可能であることが判った。
計算結果6(143Kbte)前半。
さらに、n=9999までの方程式を適用すると、
方程式に現れたものは全てHp(1)とHp(3)で表すことが可能でした。
計算結果6(143Kbte)後半。
( つまりほぼ間違いなくdinKV‘3=2 である。)
特に後で用いる関係を取り出すと、 下記が成立しています。
Hp(8)=-217Hp(1)+27Hp(3) --------------(1)
Hp(9)=-297Hp(1)+38Hp(3) --------------(2)
【非線形関係】
9p3=p3+(2p)3ですから
Hp(9)=(f(p) 3+f(2p) 3) 3=Hp(1) +Hp(8)+3f(p) 3*f(2p) 3*( f(p) 3+f(2p) 3))
移項して両辺3乗すると、下記同次3次式の方程式が得られます。
(Hp(9)-Hp(1)-Hp(8)) 3=27Hp(1)Hp(8)Hp(9) ----(3)
Hp(1)=Sをパラメータとして(1)(2)(3)を整理すると Hp(3) の3次方程式ですが、
そのうち一つの解はHp(3)=27Sであることが判っていますから、実質2次方程式です。
代入して計算すると、方程式は
(1331Hp(3)2-21168S*Hp(3)*S+84132*S2)*(Hp(3)-27*S)=0 です。
即ち、 Hp(3)= 27*S | 6*S*(1764±√1149)/1331です。
√1149は無理数です。
よって、Hp(3)=27*S です。
【結論】
以上で計算結果6から少なくともn=5316以下では
Hp(n)=n*Hp(1)の関係にあることが判ります。
5316以下には (2、4、8),(3、9、27),(5、25、125)
および900=(2*3*5)2以下の数が含まれています。
よって限定的線形関係がp=2、3、5には再帰的に適用可能であり、
因数が2、3、5のみのnにおいて値がHp(1)より確定でます。
つまり、Hp(1)が既知であれば
Hp(2a3b5c)= 2a3b5c*Hp(1),a,b,c∈N0 です。
もう少し計算すれば44100=(2*3*5*7)2以下でも成立して、
因数7を持つものも含めて成立し、すっきりすると思われますが、
N=9999では、6300=(2*3*5)2*7以下が判っているだけです。
一方(7、49、343)は判っています。
従って、数学的帰納法により、下記までが判ります。
Hp(2a3b5c7d)= 2a3b5c7d*Hp(1),a,b,c,d∈N0 ----(4)
ただし、 a≡b≡c≡0 mod 3 または d≡0 or 1 mod 3
次に、限定的線形関係を用いずに方程式を解けば、
少なくとも5316以下のnに対して
Hp(n)をHp(1)〜Hp(8)の線形結合で表せることが判ります。
計算結果6(143Kbte)中央参照。
1〜8のうち、7以外は全部2、3、5のみを因数に持ち(4)により確定しています。
限定的線形関係を用いた場合の結果から7の1乗のものも判っています。
従って、計算結果6より、n=49 が確定します。
即ち、(4)式が制限無しに適用できます。
以下、前回の解答と同じです。
【Z:整数の場合】
以上の議論で用いた関係は 領域が整数の場合にも適用されるものばかりです。
また 0=n3+(-n)3 よりHp(-n)=-Hp(n)です。
よって整数領域でも恒等変換のみです。
【Q:有理数の場合】
Hp(n)のpとして p=1/d を用いても前述の線形および限定的線形関係の証明は影響されません。
また、非線形関係(3)はHp()の同次3次式であり、やはり適用可能です。
さらにHp(3)=27Hp(1)に限定する根拠は他が無理数であることでしたから同様に限定されます。
従って、H1/d(d3)=d3H1/d(1)=H1(1) を用いることにより
H1/d(1)=1/d3です。
即ちQにおいても恒等変換のみです。
ただし、予想1が成立するとの前提の元でです。
なお、Q上だけを証明する場合、予想は次のように条件を緩和できます。
予想Q.
任意の素数p≧17に対して,その素因数(負の冪を許容)がpより小さい有理数x, y, zが存在して,
p3 = x3+ y3+ z3.
◆愛知県 Y.M.Ojisan さんからの解答。
【3次の場合の線形関係生成式】
2次の場合 恒等式 (3a+4b)2+(4a-3b)2=(5a)2+(5b)2 等があって、証明が可能でした。
予想Qは条件が緩くなっており、もしかしてと思い、3次の場合についてそのような恒等式がないか検討しました。
問題3の証明にはつながりませんでしたが、興味ある結果が得られました。
専門家からは楕円曲面の焼き直しとして一刀両断かもしれませんが。
なお、以降では対称性を重視してA3+B3+C3+D3=0 で考えます。
【定義】
(1)A3+B3+C3+D3=0 A,B,C,D∈Z である(A,B,C,D)の集合をTとする。
(2)T2→Z2の関数{ }を次のように定義する。
t1=(A1,B1,C1,D1)∈T,t2=(A2,B2,C2,D2)∈T
{t1,t2}=(A12*A2+B12*B2+C12*C2+D12*D2,A1*A22+B1*B22+C1*C22+D1*D22)
(3) t=(A,B,C,D)/GCD(A,B,C,D)を
t=<A,B,C,D>であわらす。
ただし、GCDは|A|,|B|,|C|,|D|が最大のものの符号をとり、最大が0の場合は1とする。
(4) t=(A,B,C,D)∈Tに対して [t]=(a,b,c,d) は
<A,B,C,D>の要素を次の規則に当てはまるように置換したものである。
a≧b≧c≧d & a≧|d|
【生成式補題1】
t=(A、B、C、D)∈T であるとき 整数*t∈T
*:スカラー積
【生成式補題2】
t=(A、B、C、D)∈T であるとき (A、B,C,Dの置換)∈T
【生成式補題3】
t1,t2∈Tであるとき (p、q)∈Z2 を用いて t=(p、q)・(t1;t2)∈Tである。
ここで (-p,q)={t1,t2}
(・:行列積 、;:次を下に入れる意味)
また、この生成方法を t= t1△t2 であらわす。
∵代入して計算すればよい。詳細略。
【生成式補題4】
t1,t2∈Tで t= <t1△t2> とするとき 補題3と1よりt∈Tであり、
t1= <t△t2> t2=<t△t1> である。
∵代入して計算すればよい。詳細略。
【生成式補題5】
(p,q,−q,−p)∈T ただし、p,q∈Z である。
これらの集合をW⊂Tとする。
【生成式補題6】
t0∈T 、[t0]∈Wでない、 w(p,q)∈W pq≠0 から
生成式補題4により t(p,q)=<t0△w(p.q)>∈T を作成するとき
<t(p,q)>≠<t(p’,q’)> となるp’,q’は
<w(p,q)>=<w(p’,q’)> を除き高々2個である。
また [<t(p,q)>] ∈Wでない
∵計算するとそのようなp’,q’の比は2次方程式を満足しなければならず、高々2個です。
(注記:実際にM=9999までの計算結果1でみると、判別式が開平できるものはないようです。つまり実際は0個らしい。)
生成式補題5は「線形方程式」を作り出すものとしては役に立ちませんが、生成式補題6と組み合わせることにより、p,q2個(次元)をパラメータとして、Tの要素で「線形方程式」を作るのに役立つ関係を、殆ど重複することなく生成できることがわかりました。
ただし、全てのTの要素を生み出せるということではありません。
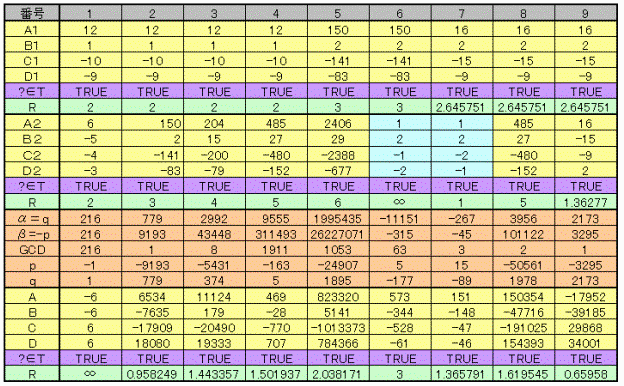
下表は生成式補題3、4により色々作ってみたものです。
番号6、7は生成式補題6の例となります。
なお、R値の意味は補題7参照。

【生成式補題7】
t10∈T t10=(A10,B10,C10,D10) であって
R=√{−(B10+D10)/(A10+C10)} ∈Q であるとき、
tpq=( (A10p2+Epq−C10q2), (B10p2+Fpq−D10q2),( C10p2−Epq−A10q2),( D10p2−Fpq−B10q2))∈T である。
ここでE=(B10-D10)*R,F=(C10-A10)/R,p,q∈Z (Qでもよい)
なおこの操作を今後 tpq=V[t10](p,q) であらわす。
∵計算すると (p2−q2) でくくれる式が出てきて、
t10∈Tを適用すると恒等的に0である事がわかる。
さてそのようなt10が存在するかどうかが問題であるが、計算結果1のデータをチェックするとかなり多数存在していることが判った。
以下に代表例を示す。
なぜかE Fはかなりの率で整数である。
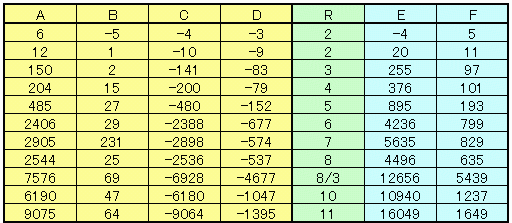
実際に、(12、1、−10、−9)→R=2,E=20、F=11に対して適用した例を下表に示す。
R値がほぼ保持されることがわかる。
例外はp=qの場合であって、Rが定まらず、かつ有効な線形方程式が得られない組み合わせになっている。
また −p,−qとp,qは同じ値である。
なお、以降 Rが定まらない場合をR=∞で表すこととする。
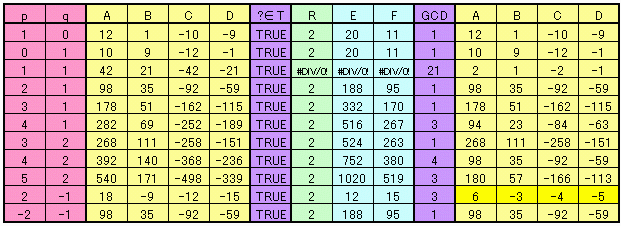
【生成式補題8】
あるt∈T に対して 生成式補題7のR値が有限で、
R(t)≠∞のものの集合をT(R(t))⊂T とするとき、
|p|≠|q|ならば V[t](p,q)∈T(R(t)) である。
∵ Apq+Cpq=(p2−q2))*(A10+C10)
Bpq+Dpq=(p2−q2)*(B10+D10) であるので。
【生成式補題9】
あるt∈T に対して、
{V[V[t](p,q)](r,s)|(p,q),(r,s)∈Z2x}⊂T[t]⊂T(R(t)) である。
ここで T[t]={V[t](u,v)|(u,v)∈Z2x}
Z2x={(u,v)|u,v∈Z & |u|≠|v|} である。
∵生成式補題8よりV[t](p,q)∈T(R(t))であるから
R(V[t](p,q))∈Qである。
よって、V[V[t](p,q)](r,s)∈Qが存在する。代入して計算すると、
V[V[t](p,q)](r,s)=V[t](u,v)]
u=(p*r+q*s)、v=(p*s+q*r)∈Z である。
【生成式補題10】
V[V[t](p,q)](r,s)=V[t](u,v)] を(p,q)∈Z2xにおける演算×と考えた場合、
{ (p,q)×(r,s)=(u,v) } ×は可換であり、単位元は(1,0)である。
またp,q∈Qで考えた場合 (p,q) |p|≠|q|の逆元が存在して
それは(p/(p2-q2),-q/(p2-q2))である。
因みに「×」は、虚実数上の積と同じ働きをもつ。
(( 虚実数=x+y*ρ ρ≠±1 ρ2=1 x,y∈実数))
∵u=(p*r+q*s)、v=(p*s+q*r)
【生成式補題11】
V[t](s,t)は tとw(p,q)∈Wを用いて補題3、4の方法でも生成することが可能である。
ただし、現実に計算する場合、後者はかなり大きな公倍数を持っており、
V[t](s,t)で計算するほうが効率的である。
一方、前者は後者の全てを生成できるわけではない。
∵代入して計算すればよい。詳細略。
【生成式補題まとめ】
生成式補題6で既約化しないで生成した場合、生成式はp、qの2次式であるため、p、q2パラメータで振っても、p、qが大きくなると疎らになり、全てをカバーするのは困難である。
一方、次元的には同じオーダーであり、実際にPCで確かめてみると、予想Qの成立に必要な、素数を下位素数冪のみの項で表記できる線形関係のうちの一定の割合をp、qが大きくなってもカバーしていることがわかった。
従って、既約化により密度が上昇すれば全体をカバーできる可能性がある。
生成式補題7によれば、生成式補題6で得た場合はかなり上のほうから既約化により落ちてくる関係を効率的に計算できる。
そこで、
(1)生成式補題7のp、qを広く振って(〜300)種となるtを生成する。
(2)生成式補題1〜2により容易にわかる関係を生成する。
(3)これらを出発点とし、生成式補題6においてp、qを若干ずつ振って(〜25)種を生成する。
(4)さらに、それらを種に(2)〜(3)を繰り返す。
という方法で線形関係をどのくらいカバーできるか、PCで計算してみた。
その結果、少なくとも計算結果1で示したM=9999以下のN0での線形関係の100%をカバーしていることを確認した。
【感想】
数学的には補題6の方法のみで、現実的には補題6と補題7の組み合わせで全ての線形関係を求めることができそうな感じがします。
そこから本題の証明にもつながるのではとは思いますが、私には難しいですね。
ちょうど学生時代に4色問題が計算機によりelephantに解かれて以来、計算機で数学することを趣味にしてきましたが、計算機の進歩もあるものの、これほど楽しませていただいた問題はなかったですね。