仧愇愳導丂Takashi丂偝傫偐傜偺夝摎丅
佱嘥佲
恾宍偺栤戣傪倱栤丄悢偺栤戣傪倲栤梊廗偟偰偄偔丅
亂倱,倲偼惍悢丄侽亝倱亝係丄侽亝倲亝係亃
係栤偺栤戣偐傜俀栤弌戣偝傟傞偲偒丄弌戣偝傟傞栤戣偺慻崌偣偺悢偼丄俇捠傝丅
亙z@亜
丂倱亖侽偺偲偒丄
梊廗傪偟偰偄側偄偺偱栤戣偼夝偗側偄丅
傛偭偰丄婜懸抣亖侽
亙zA亜
丂倱亖侾偺偲偒丄
梊廗偟偨栤戣偑侾戣弌戣偝傟傞慻崌偣偼丄俁捠傝丅
梊廗偟偨栤戣偑侽戣弌戣偝傟傞慻崌偣偼丄俁捠傝丅
傛偭偰丄
丂婜懸抣
| 亖俀俆亊 | 俁 俇 |
亄侽亊 | 俁 俇 |
| 亖侾俀丏俆 |
亙zB亜
丂倱亖俀偺偲偒丄
梊廗偟偨栤戣偑俀戣弌戣偝傟傞慻崌偣偼丄侾捠傝丅
梊廗偟偨栤戣偑侾戣弌戣偝傟傞慻崌偣偼丄係捠傝丅
梊廗偟偨栤戣偑侽戣弌戣偝傟傞慻崌偣偼丄侾捠傝丅
傛偭偰丄
丂婜懸抣
| 亖俆侽亊 | 侾 俇 |
亄俀俆亊 | 係 俇 |
亄侽亊 | 侾 俇 |
| 亖俀俆 |
亙zC亜
丂倱亖俁偺偲偒丄
梊廗偟偨栤戣偑俀戣弌戣偝傟傞慻崌偣偼丄俁捠傝丅
梊廗偟偨栤戣偑侾戣弌戣偝傟傞慻崌偣偼丄俁捠傝丅
傛偭偰丄婜懸抣亖俁俈丏俆
亙zD亜
丂倱亖係偺偲偒丄
梊廗偟偨栤戣偑俀戣弌戣偝傟傞慻崌偣偼丄俇捠傝丅
傛偭偰丄婜懸抣亖俆侽
倱傕倲傕忦審偼摨偠側偺偱丄
z@乣zD傛傝岠棪偼偳傟傕摨偠偱丄侾俀丏俆
摎丏恾宍傕悢傕丄侾栤埲忋梊廗偟偰偄偗偽壗栤梊廗偟偰傕岠棪偼摨偠偱偁傞丅
佱嘦佲
恾宍偑俇栤偐傜俀栤丄悢偑俀栤偐傜俀栤弌戣偝傟傞偲偡傞偲丄悢偺栤戣偼丄俀栤偲傕梊廗偟偰偄偔傋偒偱偁傞丅
恾宍偺栤戣傪倱栤梊廗偟偰偄偔偲偒偺摼揰偺婜懸抣傪丄俵(s)偲偡傞偲丄
栤嘥偲摨條偵丄
俵(0)亖侽
俵(1)亖俉丏俁俁丒丒
俵(2)亖侾俇丏俇俇丒丒
俵(3)亖俀俆
俵(4)亖俁俁丏俁俁丒丒
俵(5)亖係侾丏俇俇丒丒
俵(6)亖俆侽
| 傛偭偰丄俵(s)亖 | 俆侽 俇 |
亊倱 |
岠棪偼丄
乮俵(s)亄俆侽乯亐乮倱亄俀乯
亖俉丏俁俁丒丒{乮俁俁丏俁俁丒丒乛乮倱亄俀乯乸
倱亖侽偺偲偒丄嵟戝抣丂俀俆
摎.悢偺栤戣傪俀栤丄梊廗偟偰偄偔偲岠棪偑俀俆偱嵟戝偲側傞丅
佱嘨佲
| 俠乮a,b乯亖 | 倎両 (倎亅倐)両倐両 |
俉栤偁傞梊憐栤戣偺拞偐傜倱栤梊廗偟偰偄偔偲偒丄
摼揰偺婜懸抣傪倃乮倱乯偲偡傞丅
亂倱偼惍悢丄侽亝倱亝俉亃
俉栤偁傞梊憐栤戣偐傜係栤傪弌戣偡傞慻崌偣偼丄
俠乮8,4乯亖俈侽捠傝丅
梊廗偟偨栤戣偐傜倲栤丄
梊廗偟偰偄側偄栤戣偐傜乮係亅倲乯栤弌戣偝傟傞慻崌偣傪
倖乮s,t乯偲偡傞偲丄
亂倲偼惍悢丄侽亝倲亝係,倱亅係亝倲亝倱亃
倖乮s,t乯亖俠乮s,t乯亊俠乮8-s,4-t乯
| 倱 儼 t=0 | 倖(s,t)亖俈侽 |
| 倃(s)亖 | 倱 儼 t=0 | [{倖(s,t)亐俈侽}亊俀俆倲] |
| 倃(s)亖 | 4 儼 t=s-4 | [{倖(s,t)亐俈侽}亊俀俆倲] |
亙倎亜
倱亖侽偺偲偒丄倖(0,0)亖俈侽
(1)傛傝丄倃(0)亖侽
亙倐亜
倱亖侾偺偲偒丄
倖(1,0)亖倖(1,1)亖俁俆
(1)傛傝丄倃(1)亖侾俀丏俆
亙們亜
倱亖俀偺偲偒丄
倖(2,0)亖倖(2,2)亖侾俆丄倖(2,1)亖係侽
(1)傛傝丄倃(2)亖俀俆
亙倓亜
倱亖俁偺偲偒丄
倖(3,0)亖倖(3,3)亖俆丄
倖(3,1)亖倖(3,2)亖俁侽
(1)傛傝丄倃(3)亖俁俈丏俆
亙倕亜
倱亖係偺偲偒丄
倖(4,0)亖倖(4,4)亖侾丄
倖(4,1)亖倖(4,3)亖侾俇丄
倖(4,2)亖俁俇
(1)傛傝丄倃(4)亖俆侽
亙倖亜
倱亖俆偺偲偒丄
倖(5,1)亖倖(5,4)亖俆丄
倖(5,2)亖倖(5,3)亖俁侽
(1)傛傝丄倃(5)亖俇俀丏俆
亙倗亜
倱亖俇偺偲偒丄
倖(6,2)亖倖(6,4)亖侾俆丄
倖(6,3)亖係侽
(1)傛傝丄倃(6)亖俈俆
亙倛亜
倱亖俈偺偲偒丄
倖(4,3)亖倖(4,4)亖俁俆
(1)傛傝丄倃(1)亖俉俈丏俆
亙倝亜
倱亖俉偺偲偒丄倖(8,4)亖俈侽
(1)傛傝丄倃(8)亖侾侽侽
傛偭偰丄
倃(s)亐倱亖侾俀丏俆
侾栤埲忋梊廗偡傟偽壗栤梊廗偟偰傕丄岠棪偼摍偟偄丅
亙姶憐亜
僥僗僩曌嫮傪偟偰傕柍堄枴偵尒偊傞寢壥偑弌偰偄傞條偱偡丅
俙孨偼岠棪傪峫偊偰偄傞傂傑偑偁偭偨傜慡晹偺栤戣傪廫暘偵棟夝偱偒傞傑偱曌嫮偡傞傋偒偱偟傚偆丅
仧搶嫗搒丂朠丂墱恖丂偝傫偐傜偺夝摎丅
仸奺恾偺昞偼Microsoft Excel偱嶌惉偟偨傕偺偱偡丅
偦偺偨傔丄暥拞偱偼暘悢偱昞婰偝傟偰偄傞傕偺偑昞拞偱偼彫悢昞婰偵側偭偰偄傑偡丅
偛椆彸壓偝偄丅
亂栤戣侾亃
梊憐栤戣偼偳偪傜傕係栤偢偮偱偡偹丅
梊憐栤戣係栤偺偆偪弌戣偡傞俀栤傪慖傇慖傃曽偼
慡晹偱4俠2亖俇捠傝丅
仠傑偢丄侾栤偩偗曌嫮偟偨応崌丄
偦偺侾栤傪娷傓弌戣曽朄偼俇亅3俠2亖俁捠傝丅
乮偦偺侾栤偑娷傑傟側偄弌戣曽朄偺悢傪堷偔乯
| 妋棪偼 | 3 6 | 丅 |
| 傛偭偰婜懸抣偼25亊 | 3 6 |
亖12.5丅 |
曌嫮偟偨栤戣侾栤偁偨傝12.5丅
仠俀栤曌嫮偟偨応崌丄
偦偺俀栤偑偢偽傝弌戣偝傟傞弌戣曽朄偼傕偪傠傫侾捠傝丅
| 妋棪偼 | 1 6 | 丅 |
傑偨丄俀栤偺偆偪侾栤偩偗偑偁偨傝偲側傞弌戣曽朄偼丄弌戣偝傟偨傕偆侾栤偑曌嫮偟側偐偭偨俀栤偺偳偪傜偐偵側傞偐傜
俀亊俀亖係捠傝丅
| 妋棪偼 | 4 6 | 丅 |
| 傛偭偰婜懸抣偼50亊 | 1 6 |
亄25亊 | 4 6 |
亖25丅 |
仠俁栤曌嫮偟偨応崌丄
偦偺偆偪偺俀栤偑偢偽傝偁偨傝偱偁傞弌戣曽朄偼3俠2亖俁捠傝丅
| 妋棪 | 3 6 |
侾栤偩偗偑偁偨傝偱偁傞弌戣曽朄偼傗偼傝俁捠傝丅
| 妋棪 | 3 6 |
| 傛偭偰婜懸抣偼50亊 | 3 6 |
亄25亊 | 3 6 |
亖37.5丅 |
仠係栤曌嫮偟偨応崌丄
偦偺偆偪偺俀栤偑偁偨傝偱偁傞弌戣曽朄偼摉慠俇捠傝丅
| 妋棪 | 6 6 |
| 傛偭偰婜懸抣偼50亊 | 6 6 |
=50丅 |
侾栤傕曌嫮偟側偐偭偨応崌偼峫偊傞傑偱傕側偔婜懸抣偼僛儘丅
偙傟傪傕偲偵丄恾宍偺栤戣丒悢偺栤戣傪壗栤曌嫮偟偨偐偵傛傞侾栤偁偨傝偺婜懸抣傪偼偠偒偩偟偨偺偑壓恾偱偡丅

寁嶼曽朄偼乽乮恾宍栤戣偺婜懸抣亄悢栤戣偺婜懸抣乯亐乮恾宍栤戣悢亄悢栤戣悢乯乿偱偡丅
岠棪揑偵偼丄乽慡栤戣傪偁偒傜傔傞乿偺偱側偗傟偽丄偳偪傜偺暘栰傪壗栤曌嫮偟傛偆偑岠棪偼曄傢傜側偄偲偄偆偙偲偵側傞傛偆偱偡丅
偱偁傟偽丄慡栤曌嫮偟偰枮揰傪慱偆偺偑嵟椙偺嶔偩偲巚偄傑偡乮徫乯丅
亂栤戣俀亃
侾乯恾宍栤戣曇
弌戣偡傞俀栤偺慖傃曽偼6俠2亖15捠傝丅
仠侾栤曌嫮偟偨偲偡傞偲丄偦偺侾栤傪娷傓弌戣曽朄偼俆捠傝丅
乮傕偆侾栤傪巆傝俆栤偺拞偐傜慖傇偐傜乯
| 妋棪偼 | 5 15 |
丅 |
| 婜懸抣偼25亊 | 5 15 |
亖 | 25 3 |
丅 |
仠俀栤曌嫮偟偨偲偡傞偲丄
| 偦偺俀栤偲傕弌戣偝傟傞妋棪偼 | 1 15 |
丅 |
| 妋棪 | 8 15 |
丅 |
| 傛偭偰婜懸抣偼50亊 | 1 15 | 亄25亊 | 8 15 |
亖 | 50 3 |
丅 |
仠俁栤曌嫮偟偨偲偡傞偲丄偦偺偆偪俀栤偑偁偨傝偱偁傞弌戣曽朄偼
偳偺俀栤偑偁偨傝偐偱3俠2亖俁捠傝丅
| 妋棪 | 3
15 |
丅 |
侾栤偩偗偑偁偨傝偱偁傞弌戣曽朄偼丄
偳偺侾栤偑偁偨傝偐偱俁捠傝亊弌戣偝傟傞傕偆侾栤偺慖傃曽俁捠傝亖俋捠傝丅
| 妋棪 | 9 15 |
丅 |
| 傛偭偰婜懸抣偼50亊 | 3 15 | 亄25亊 | 9 15 |
亖 | 75 3 |
丅 |
仠係栤曌嫮偟偨応崌丄峫偊曽偼俁栤偺応崌偲摨條偩偐傜
| 俀栤偑偁偨傝偱偁傞妋棪偼 | 6 15 |
丅 |
| 侾栤偩偗偁偨傝偱偁傞妋棪偼 | 8 15 |
丅 |
| 傛偭偰婜懸抣偼50亊 | 6 15 | 亄25亊 | 8 15 |
亖 | 100 3 |
丅 |
仠俆栤曌嫮偟偨応崌丄峫偊曽偼傗偼傝俁栤偺応崌偲摨條偩偐傜
| 俀栤偑偁偨傝偱偁傞妋棪偼 | 10 15 |
丅 |
| 侾栤偩偗偁偨傝偱偁傞妋棪偼 | 5 15 |
丅 |
| 傛偭偰婜懸抣偼50亊 | 10 15 | 亄25亊 | 5 15 |
亖 | 125 3 |
丅 |
仠俇栤曌嫮偟偨応崌丄愨懳偦偺拞偺俀栤偑弌戣偝傟傞丅
妋棪100亾丅
婜懸抣偼摉慠50丅
俀乯悢偺栤戣曇
梊憐栤戣偑俀栤偲偄偆偙偲偼丄杮斣傕偦偺俀栤偑昁偢弌傞偙偲偵側傝傑偡丅
侾栤偩偗曌嫮偟偨応崌丂婜懸抣俀俆
俀栤偲傕曌嫮偟偨応崌丂婜懸抣俆侽
偙傟傪傕偲偵丄恾宍偺栤戣丒悢偺栤戣傪壗栤曌嫮偟偨偐偵傛傞侾栤偁偨傝偺婜懸抣傪偼偠偒偩偟偨偺偑壓恾 偱偡丅
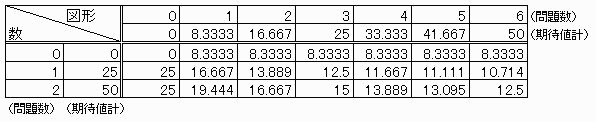
寁嶼曽朄偼乽乮恾宍栤戣偺婜懸抣亄悢栤戣偺婜懸抣乯亐乮恾宍栤戣悢亄悢栤戣悢乯乿偱偡丅
偙傟偵傛傞偲乽恾宍栤戣侽栤丄悢偺栤戣侾栤傑偨偼俀栤乿乮婜懸抣俀俆乯偑堦斣岠棪偑偄偄傛偆偱偡丅
亂栤戣俁亃
曌嫮偡傞栤戣傕丄恾宍丒悢偵偐偐傢傝側偔偰偄偄傫偱偡傛偹丅
弌戣偡傞栤戣偺慖傃曽偼8俠4亖70捠傝丅
値栤曌嫮偟偨応崌偺婜懸抣偺媮傔曽偼埲壓偺捠傝丅
侾乯値亖侽丂偺偲偒丂婜懸抣偼傕偪傠傫僛儘丅
俀乯侾亝値亝係丂偺偲偒
曌嫮偟偨値栤拞倠栤乮侾亝倠亝値乯偑娷傑傟傞弌戣曽朄偼
n俠k亊8-n俠4-k 捠傝側偺偱丄倠偺奺抣偵偮偄偰弌戣僷僞乕儞悢傪媮傔丄倠偺抣偵墳偠偨婜懸抣傪嶼弌丅
俁乯俆亝値亝俉丂偺偲偒
曌嫮偟偨値栤拞倠栤乮侾亝倠亝係丄倠亞値亅係乯偑娷傑傟傞弌戣僷僞乕儞偼
n俠k亊8-n俠4-k 捠傝丅
埲壓丄俀乯偲摨條丅
仸倠亞値亅係側偺偼丄乽曌嫮偟側偐偭偨栤戣偐傜偺弌戣悢乮係亅倠乯乿偑
丂乽曌嫮偟側偐偭偨栤戣偺憤悢乮俉亅値乯乿傪挻偊偰偼偄偗側偄偐傜偱偡丅
壓恾 偼忋偱媮傔偨値(曌嫮悢)偲倠(揑拞悢)偺抣偵傛傞弌戣僷僞乕儞悢偲丄偦偙偐傜媮傔偨侾栤偁偨傝偺婜懸抣偺昞偱偡丅
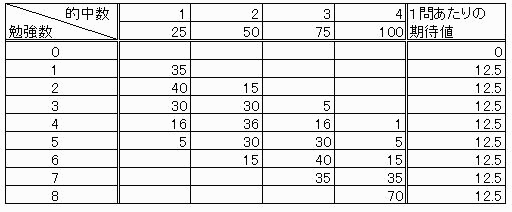
偡偭偐傝偁偒傜傔偰偟傑偆偺偱側偗傟偽丄岠棪偲偟偰偼壗栤曌嫮偟偰傕曄傢傜側偄傛偆偱偡丅
栤戣侾偲摨條丄慡栤曌嫮偟偰枮揰傪慱偆偺偑嵟忋偺傛偆偱偡丒丒丒