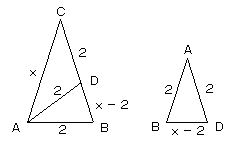
仧惷壀導丂儓僢僔乕 偝傫偐傜偺夝摎丅
亂栤戣侾亃
| 1 13 | =076923 076923 丒丒丒 |
333 愡栚偺嵟屻偺 3 偑 彫悢戞1998埵側偺偱丄
2000 斣栚偼 俈 偱偡丅
摎偊丂俈
亂栤戣俀亃
恾偵偍偄偰丄
佢俙亖佢俛亖俈俀亱丄佢俠亖俁俇亱偱偡丅
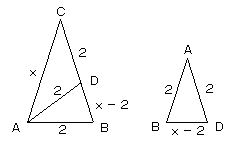
佢俙偺俀摍暘慄偲俛俠偺岎揰傪俢偲偡傞偲丄
丂佢俢俙俛亖俁俇亱丄佢俙俢俛亖俈俀亱
傛傝丄仮俙俛俠偲仮俛俢俙偼憡帡偵側傝傑偡丅
俙俠亖俛俠亖倶丂偲偍偔偲丄俢俛亖倶亅俀
傑偨丄俙俛亖俙俢亖俀
曈偺斾棪傪昞偡偲丄
丂倶丗俀亖俀丗倶亅俀
傛傝丄
倶乮倶亅俀乯亖係
倶亜侽偱偙傟傪夝偔偲丄
丂倶亖侾亄![]() 丂丒丒丒丂摎偊
丂丒丒丒丂摎偊
http://www.geocities.co.jp/Playtown-Dice/5061/sansu/pentadraw.htm 偺壓偺曽傕偛棗壓偝偄丅
仧媨忛導丂傾儞僷儞儅儞 偝傫偐傜偺夝摎丅
亂栤戣侾亃
| 1 13 | =0.0769230769... |
2000亖6*333+2
2000斣栚亖俈
亂栤戣俀亃
| 佢A亖 | 2兾 5 |
丂AC
| 亖2sin( | 2兾 5 | )/sin( | 兾 5 | ) |
| 亖4cos( | 兾 5 | ) |
| 亖 |
仧愇愳導丂柪偊傞梤 偝傫偐傜偺夝摎丅
亂栤戣侾亃
| 侾 侾俁 | 偼丄弞娐彫悢偱偁傞丅 |
| 侾 侾俁 |
| 亖 | 俈俇俋俀俁 俋俋俋俋俋俋 |
| 亖俈俇俋俀俁丒 | 亣 嚁 n=1 | 乮侾侽-6n乯 |
| 亖侽丏侽俈俇俋俀俁侽俈俇俋俀俁侽俈俇俋俀俁丒丒丒丒 |
彫悢揰埲壓侾埵偐傜俇埵傑偱偺悢帤偑弞娐偟偰偄傞丅
彫悢揰埲壓侾俋俋俉埵偺悢帤偼丄乽俁乿偲側傞偺偱丄
彫悢揰埲壓俀侽侽侽埵偺悢帤偼丄乽俈乿偱偁傞丅
亂栤戣俀亃
佢俛俙俠偺俀摍暘慄偲俛俠偲偺岎揰傪丄揰俢偲偡傞丅
佢俠俙俢亖佢俛俙俢亖佢俛俙俠乛俀 丂丂丂丂丂丂丂丂丂亖佢俙俠俢丂乮戣堄傛傝乯 佢俙俢俛亖佢俠俙俢亄佢俙俠俢 丂丂丂丂亖俀佢俙俠俢 丂丂丂丂亖佢俙俛俢埲忋偵傛偭偰丄
仮俢俠俙偼丄俢俠亖俢俙偺俀摍曈嶰妏宍偱偁傞丅丒丒亙俀亜
亙侾亜傛傝丄俙俛丗俛俢亖俙俠丗俙俛
丂俙俛亊俙俛亖俙俠亊俛俢 丂丂丂丂丂丂亖俙俠亊乮俛俠亅俠俢乯丒丒丒丒亙俁亜亙俀亜偲戣堄傛傝丄
俙俠亖侾亄![]()
仧愮梩導丂彫悪丂悞晇 偝傫偐傜偺夝摎丅
亂栤戣侾亃
| 1 13 | 偼侽丏侽俈俇俋俀俁侽俈俇俋俀俁丒丒丒丒偲丄 |
亂栤戣俀亃
佢A亖佢B亖俀佢C偱偁傝嶰妏宍偺撪妏偺榓偼侾俉侽搙偱偁傞偺偱
俀佢C亄俀佢C亄佢C亖侾俉侽搙偩偐傜丄
佢C亖侾俉侽亐俆亖俁俇搙偲側傞丅
偡傞偲佢A偺擇摍暘慄偲BC偲偺岎揰傪D偲偡傞偲丄嶰妏宍ADC偼AC傪掙曈偲偟偨擇摍曈嶰妏宍偲側傞丅丒丒丒(1)丂
戣堄傛傝丄AD亖俀偩偐傜丄(1)傛傝CD=俀偲側傞丅
傑偨(1)傛傝丄
佢ADC=180搙-36搙*2=108搙偲側傝丄佢ADB偼72搙偲側傞丅
傛偭偰丄嶰妏宍ADB傕擇摍曈嶰妏宍偲側傝丄AB=俀偲側傞丅
偙偙偱BD=倶偲偟丄嶰妏宍ABC偲嶰妏宍ABD偺斾傛傝
乮CB:AD亖AB:BD乯仺2亄倶丗2=2:x仺4=2x+x*x偲側傝夝偺岞幃偐傜
x=-1+![]() 乮x亜0)偩偐傜
乮x亜0)偩偐傜
AC=BC=CD+DB偐傜丄丂AC=2-1+![]() =1+
=1+![]()
亂栤戣俁亃
壓偵撌側曻暔慄偵側傞偲峫偊傜傟傞偺偱丄幉偺y嵗昗偼俀偱偁傝
俇亅俀亖係偐傜俀亅係亖亅俀偐傜
傕偆傂偲偮偺岎揰偺嵗昗偼乮侽丄亅俀乯
仧媨忛導丂傾儞僷儞儅儞 偝傫偐傜偺夝摎丅
亂栤戣俁亃
(0,2*2-6)=(0,-2)
亂栤戣係亃
x2=8y, 2y=x+24
x2-4x-96=0,
x=12,-8, y=18,8
(x,y)=(12,18),(-8,8)
仧搶嫗搒丂妺堖丂墱恖 偝傫偐傜偺夝摎丅
亂栤戣侾亃
| 1 13 | =0.0769230769230762930...丂偱丄 |
侾偺偲偒侽丄俀偺偲偒俈丄俁偺偲偒俇
係偺偲偒俋丄俆偺偲偒俀丄侽偺偲偒俁偱偡丅
偙傟偵傛傝丄彫悢揰埲壓戞2000埵偼俈偱偡丅
亂栤戣俀亃
佢俙偺擇摍暘慄偲俛俠偺岎揰傪俢偲偡傞偲丄
佢俛亖佢俛俙俢亖佢俠俙俢
佢俙亖佢俛亖佢俙俢俛
偙傟傜偐傜丂俙俢亖俠俢亖俙俛亖俀
傑偨仮俙俛俠偲仮俛俢俙偼憡帡
偲偄偆傢偗偱丄俛俠丗俙俢亖俙俛丗俛俢
偩偐傜
俛俢亄俠俢丗俙俢亖俙俛丗俛俢
俛俢亄俀丗俀亖俀丗俛俢
乮俛俢亄俀乯亊俛俢亖係
俛俢2亄俀俛亅係亖侽
俛俢亜侽偩偐傜俛俢亖![]() 亅侾
亅侾
埲忋傛傝丄俙俠亖俛俠亖俛俢亄俠俢亖![]() 亄侾
亄侾
亂栤戣俁亃
偙偺曻暔慄偼倶亖倎(倷亅俀)2亅係偲彂偗傞丅乮倎偼幚悢乯
| 偙傟偑乮侽丆俇乯傪捠傞偐傜丄倎亖 | 1 4 |
倶亖侽偺偲偒丄(倷亅俀)2亖侾俇丂偲側傞偑
戣堄傛傝倷亗俇側偺偱丄倷亖亅俀
摎偊丗乮侽丆亅俀乯
仧搰崻導偺拞妛峑俁擭惗丂巟棧柵楐 偝傫偐傜偺夝摎丅
亂栤戣侾亃
1/13傪偟丄偦偺夝偑0.076923乧乮埲屻偙偺孞傝曉偟乯偱偡丅
偙傟偼丄彫悢揰埲壓偑俇寘側偺偱俀000/6傪偟偰丄333梋傝俀偱偡丅
偙傟偼丄333夞076923傪孞傝曉偟丄彫悢揰俀屄嵍傪堄枴偟傑偡丅
亪俈偱偡丅