◆宮城県 アンパンマン さんからの解答。
λ(1)=1,λ(2)=2,λ(3)=3,
λ(4)=4,λ(5)=6,λ(6)=6,λ(7)=12
n＞7の場合,piをi番目の素数とし、
p3=5,p4=7,p5=11,p6=13,...
niはλ(n)がはじめてpiが出現するnとします。
n3=8,n4=14,n5=23,...
すると、
λ(ni+k)=pi λ(ni+k-pi), k=0,1,...,pi-1
λ(ni+k)=λ(ni+pi-1)=pi λ(ni-1), k=pi,...,ni+1-ni-1
◆出題者のコメント。
アンパンマンさん，早速の解答，ありがとうございます。
着眼点は非常によいと思うのですが，残念ながら反例を見つけてしまいました。
まず第1式については，不等式
λ(ni＋k)≧piλ(ni＋k−pi) (0≦k＜p)
は成り立ちますが，逆の不等式は必ずしも成り立ちません。
実際，i＝5, pi＝11, ni＝27, k＝2とおくと，
λ(ni＋k)＝λ(29)＝5*7*8*9＝2520,
piλ(ni＋k−pi)＝11λ(18)＝11*1*2*3*5*7＝2310
となります。
一方，第2式についても，それぞれ一方の不等式は成り立ちますが，逆の不等式は必ずしも成り立ちません。
実際，i＝4, pi＝7, ni＝14, k＝9とおくと
（ni＋1＝27に注意），
λ(ni＋k)＝λ(23)＝3*5*7*8＝840,
λ(ni＋pi−1)＝λ(20)＝1*3*4*5*7＝420,
piλ(ni−1)＝7λ(13)＝7*1*3*4*5＝420
となります。
二つの場合について，なぜ逆の不等式が成り立たないのかぜひ考えてみてください。
◆岡山県 藤井 さんからの解答。
λ(n)を求めるプログラムを作ってみました。
Ｃ言語です。
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
int buf[128];
char res[4096];
char ib[16];
int n;
/* ユークリッドの互除法を使って最小公倍数を求める関数 */
int lcm(int a, int b)
{
int x = a, y = b, c;
if (a <= 0 || b <= 0 || a < b) {
printf("error !!\n");
return 1;
}
while (b != 0) {
c = a % b;
a = b;
b = c;
}
return (x * y / a);
}
int main(int argc, char* argv[])
{
int nn = 128;
int i;
if (argc == 2) {
nn = atoi(argv[1]);
}
/* 1 から nn まで λ(n) を求める */
for (i = 1; i <= nn; i++) {
int m = 1;
/* 分割の初期化 */
buf[0] = i;
n = 1;
do {
int j;
int l = buf[0];
for (j = 1; j < n; j++) {
l = lcm(l, buf[j]);
}
if (m < l) {
m = l;
strcpy(res, "[");
for (j = 0;j < n; j++) {
if (j == 0) {
sprintf(ib, "%d", buf[j]);
} else {
sprintf(ib, ",%d", buf[j]);
}
strcat(res, ib);
}
strcat(res, "]");
}
if (buf[n - 1] != 1) {
buf[n - 1]--;
buf[n++] = 1;
} else {
for (j = n - 1; j >= 0; j--) {
if (buf[j] != 1) {
break;
}
}
if (j >= 0) {
int c = buf[j] - 1;
int s = buf[j] + n - j - 1;
int k;
for (k = 0; k < (s / c); k++) {
buf[j + k] = c;
}
n = j + (s / c);
if ((s % c) != 0) {
buf[j + k] = (s % c);
n++;
}
} else {
n = -1;
}
}
} while (n > 0);
printf("%3d : %4d %s\n", i, m, res);
fflush(stdout);
}
return 0;
}
実行結果
n : λ(n) 分割の例
1 : 1
2 : 2 [2]
3 : 3 [3]
4 : 4 [4]
5 : 6 [3,2]
6 : 6 [6]
7 : 12 [4,3]
8 : 15 [5,3]
9 : 20 [5,4]
10 : 30 [5,3,2]
11 : 30 [6,5]
12 : 60 [5,4,3]
13 : 60 [5,4,3,1]
14 : 84 [7,4,3]
15 : 105 [7,5,3]
16 : 140 [7,5,4]
17 : 210 [7,5,3,2]
18 : 210 [7,6,5]
19 : 420 [7,5,4,3]
20 : 420 [7,5,4,3,1]
21 : 420 [7,5,4,3,2]
22 : 420 [7,6,5,4]
23 : 840 [8,7,5,3]
24 : 840 [8,7,5,3,1]
25 : 1260 [9,7,5,4]
26 : 1260 [9,7,5,4,1]
27 : 1540 [11,7,5,4]
28 : 2310 [11,7,5,3,2]
29 : 2520 [9,8,7,5]
30 : 4620 [11,7,5,4,3]
31 : 4620 [11,7,5,4,3,1]
32 : 5460 [13,7,5,4,3]◆愛知県 Y.M.Ojisan さんからの解答。
【記号】
特に断らない限り、下記とする。
ｎ , ｍ、ｉ、ｊ ：自然数
ｐｉ ：素数列要素 ｐ１＝２ ｐ２＝３ ．．．
ｑｉ 、ｑ 、Ｑ ：非負整数列要素、非負整数列、非負整数列の集合
ｐｉ＾x ：
x＝０のとき ｐｉ＾x＝０ 、
その他のとき ｐｉ＾x＝ｐｉx
【解答 第１章 λの性質】
（１）λの性質１
λ（ｎ+1）≧λ（ｎ）
∵ 略
（２）λの性質2
∵ｐｉxがKjの２個以上に分散して存在するとき、
その最小値ｐｉxminは最小公倍数λ(n)には影響しない。
従って、
| λ(ｎ)＝λ(･･･＋Kj＋･･･)＝λ(･･･＋ | Kj ｐｉxmin | ＋･･･)＝λ(ｍ) |
一方、Kiにｐｉｑi 以外の素数冪の素因数が存在する場合、
Ki＝Ｘｐｉｑi と置くとき
Ｘｐｉｑi−(Ｘ＋ｐｉｑi)＝(Ｘ−１)(ｐｉｑi−１)−１≧１
である。
なぜなら、Ｘもｐｉｑiも素数の冪の積なので、
Ｘ≧２、ｐｉｑi≧２。
また、両者は異なる素数を含むためどちらか一方は３以上でなければならないからである。
従って
λ(ｎ)＝λ(･･･＋Ki＋･･･） ＝λ(･･･＋Ｘ＋ｐｉｑi＋･･･） ＝λ(ｍ)であり、ｎ＞ｍである。
λ(ｎ)値を与える分割方法は１つではない
（例えば [６]と[１＋２＋３]）が、そのうちここに示す分割をし、
あまり(＝ｎ−Σｐｉｑi)を１＋１＋･･･に分ける方法を正規分割と呼ぶことにする｡
（P0=1を仲間に入れたと見なせばよい。１＾ｘ＝ｘ ）
（３）探索方法
λの性質2により 各Ki を ｐｉｑiに限り探索すればよい。すなわち
（４）有効分割数 M
qｉが０でないものの数、すなわち最小公倍数に直接影響しているKiの数を有効分割数とし Mで表す｡
従って、正規分割の分割数は M＋あまり である。
【解答 第２章 高速探索】
（１）λ（i、ｎ）
λ（i、ｎ）を次のように定義する。
即ち、各Kiがｐｉ未満の素数を因数に持たないという条件のなかでの最大の最小公倍数とする。
このとき、λ（i、ｎ）は次の関係をもつ。
∵ これは１章（１）探索方法の探索順序を規定しただけである。
（２）λの性質３
λ（ｎ） ＝ λ（１、ｎ）
（３）λの性質４
λ（i、ｎ）≧ λ（i+1、ｎ）
（４）λの性質５
λ（i、ｎ）＝ １ for ｐi＞ｎ
（５）λの性質６
qｉ≦１ for ｐi＞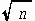
（６）λの性質７
| λ（i、ｎ）＜( | ｎ Ｌ | ) | Ｌ | for ｐi＞ |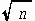
Ｌ：ｐi以上の連続素数和がｎを超えない最大の素数の個数。
∵性質６よりｐi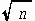＞においてはqｉ≦１であるので、ｎの正規分割時の有効分割数ＭはＬ以下である。
ｎをＬ個に分割したものの積が最大になるのは、等分割した場合のみであり、
| ( | ｎ Ｌ | ) | Ｌ | である。 |
| この関数はＬ＝ | ｎ ｅ | において最大値をとり |
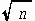でありから、L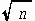＜ であり、
| ｎ≧６であれば L＜ | ｎ ｅ | である。 |
| すなわち、λ（i、ｎ）＜( | ｎ Ｍ | ) | Ｍ | ≦( | ｎ Ｌ | ) | Ｌ | である。 |
（７）高速探索手順
素数列表ｐiは既存とする。
Ａ．iの探索範囲Imaxを決めます｡
第３章の(3)式等から大体下記程度と予想される。
Imax=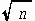 ないし ｐImax=４ 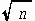（＠ n=10000前後）
前者は大きなｎでも使えると予想されるが、後者は係数の修正が必要だろう。
( 係数修正∝√ln(ｐImax /10000))
Ｂ． λ（Imax ＋１、ｎ）に、可能なら性質５により正確に、ｎが大きい場合は性質７により超えない値を設定する。
Ｃ．（第１ループ） ｎ＝２→ｎ を回す。
Ｄ．（第2ループ） ｉ＝Imax→１ を回す。
Ｅ．（第３ループ）
| ｑi＝[ | ln(n) ln(ｐi) | ]→０ を回わして第2章（１）の探索を実施。 |
この方法によれば λ（i、ｎ）の探索範囲は、i方向は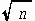の程度以下である。
また、各（i,ｎ）においてln(ｎ)回の程度の探索を行うので、
全体ではln(ｎ)*ｎ１．５のオーダーであり、計算機で容易に探索可能である。
ただし素数列作成は勘定外。
（８）計算結果
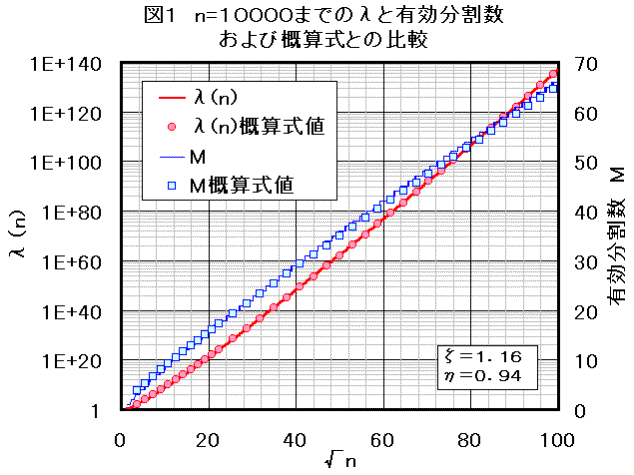
ｎ＝１００００ までの計算を実施した。結果を図１〜３に示す｡
CpuTimeは素数列表作成を含み約３秒(PC 500MHz 128MB C++)だった。
λ（ｎ）を図１、２（赤太線）に示す。
横軸は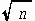にしてある。縦軸は対数スケール。
合わせて、その時の 有効分割数：Ｍ（青線）を示す。縦軸スケールは右側。
＊ 有効分割数は割合滑らかではあるが、変化点で多少チャタがある。図２
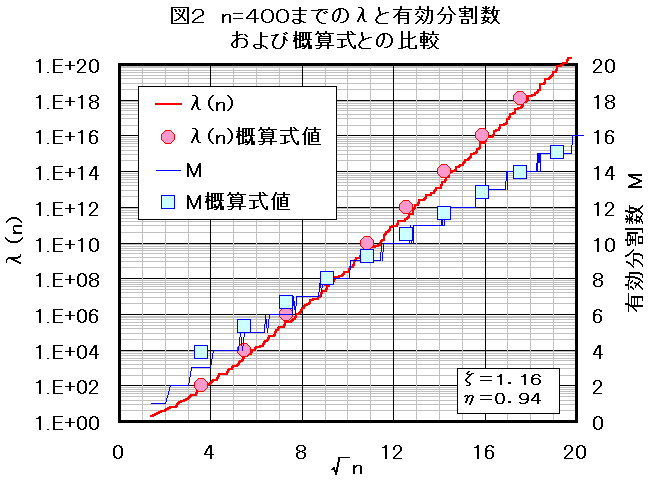
＊ 最大のKi＝Pimaxは平均的傾向はあるがかなりランダムに変動している。図３
＊ 因みに ｎ＝１００００の正規分割を下記に示す。Ｍ＝６６。Ｋ：［素数 冪数］
[ 2 6],[ 3 4],[ 5 2],[ 7 2],[ 11 2],[ 13 2],[ 17 1],[ 19 1],[ 23 1],[ 29 1], [ 31 1],[ 37 1],[ 41 1],[ 43 1],[ 47 1],[ 53 1],[ 59 1],[ 61 1],[ 67 1],[ 71 1], [ 73 1],[ 79 1],[ 83 1],[ 89 1],[ 97 1],[101 1],[103 1],[107 1],[109 1],[113 1], [127 1],[131 1],[137 1],[139 1],[149 1],[151 1],[157 1],[163 1],[167 1],[173 1], [179 1],[181 1],[191 1],[193 1],[197 1],[199 1],[211 1],[223 1],[227 1],[229 1], [233 1],[239 1],[241 1],[251 1],[257 1],[263 1],[269 1],[271 1],[277 1],[281 1], [283 1],[293 1],[307 1],[311 1],[313 1],[317 1],[あまり 9]
【解答 第３章 大きなｎの場合の概算】
大きなＰに対して、Ｐ以下の素数の数π（Ｐ）は、
| 素数定理により、 | Ｐ ln(Ｐ) | に漸近する。 |
| π（Ｐ）= | ζＰ ln(Ｐ) | ζ=1.16 |
探索範囲として 小さなｐiに対してはq i≧２もありえるが
ｐi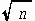＞ では１以下である。
このため 対数スケールでλを見た場合q i ≧２ になる部分の割合は小さい。
従って概算として、ｐi の小さいほうから可能な範囲で、全q i＝１ とする。
| これより Ｍ≒π（Ｐ）＝ | ζＰ ln(Ｐ) | である。 |
Pに比べln(P)の変化は非常に遅い。
そこで、概算として有効なｐi は平均的に等間隔 ζ／ln(Ｐ) でM個並んでいるとすると、Ｐをパラメータとして以下の概算式が得られる。
なお、ｎの計算式では、ｐiの分布が小さいほうに片よる分に対応して、小さく調整するためのηを掛けてある。
| （１） Ｍ＝π（Ｐ）＝ | ζＰ ln(Ｐ) |
| （２） λ(ｎ) ＝M！( | Ｐ Ｍ | ) | M | Γ（M＋１）( | Ｐ Ｍ | ) | M |
| ｎ＝η( | Ｐ Ｍ | ) | （Ｍ＋１）Ｍ ２ |
| ＝ | ηＰ（Ｍ＋１） ２ |
| ≒ | ηＭ２＊ln(Ｐ) ２ζ |
| ≒ | ηζＰ２ ln(Ｐ２) |
ｎ＝１００００以下に対し，ηをチューニングしてη＝０．９４ としたときの概算結果を図１，２に示した。
λの概算値は○印マークである。
対数スケールなので実際はかなり大雑把ではあるが、傾向は意外に全体的に一致している。
ｎが∞に近づくと ζ＝１において、ηは１付近に収束すると期待される。
| なお、 ｎ≒ | ηＭ２＊ln(Ｐ) ２ζ | と 探索結果より |
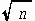として問題ないだろうと予想される。
| また、ｎ≒ | ηζＰ２ ln(Ｐ２) | 〜π(Ｐ２)から、 |
【感想】
問題の設定が漠然としていたので、自分ができる範囲に持ち込んで楽しむことができました。
【解答 第４章 補足】
（１）第２章等で Kmax=Pmax としていますが厳密には正しくありません。
実際 n=4,7,23,24,25,26,29 および
132=[8+9+25+7+11+13+17+19+23]は Kmax＞Pmax となっています。
一方 少なくとも 133≦n≦10000 では 探索の結果Kmax=Pmax が成立しており、
一般に 133≦n での成立が予想されます。
（２）n=10000まで３秒ですので、n=100万まで１時間程度となりますが、
必要メモリ容量がｎの１．５乗オーダーであるため、1000倍のメモリが必用であり、普通のPCの能力を超えます。
しかし、（１）が正しければ、Pmax程度以前のｎにおける値を記憶する必要がなくなり、
メモリー容量を「ｎ」のオーダーに減少でき、n=100万程度まで計算可能になります。
| （３）「 | Imax |
(ｐi≧ｎである最小の ｐImax)≧K2max for n＞4 」 |
（４）実際にPCで探索する場合、Imaxの場合と同様に予想を簡単に確認する方法があるので（３）は必ずしも必要ではありません。
その方法は、以下です。
| λ（i、ｎ）＜( | ｎ Ｌ | ) | Ｌ |
n＝10000まで、この手法で同じ結果が得られることを確認していますが、100万までの計算は行っていません。
（Pmax=355を用いた）
【解答 第５章 大きなｎのＰＣ探索】
第４章の方法で ｎ＝３３０万 までコアメモリ内で計算することができました。
計算時間は約１時間でした。
１週間くらい使えばｎ＝１０8ぐらいまで計算できそうです。
ただし、外部記憶装置を使わないとできないので工夫が必要です。
実際単純に仮想メモリを使うと、ＨＤへの頻繁なアクセスで、全く進みません。
本問題は探索する上では非常に扱いやすい構造を持っています。
第４章で示したようにｎおよびｑの方向にはＰｍａｘの程度以前の探索は不要です。
（推定ではありますが）
また、Imax (ｐi)の方向は 一つ前だけが必要です。
以上からＨＤへのアクセスを最小限にして探索する方法として、図４のようにImax方向を幾つかにわけ、ΔimaxごとにＰmaxづつバッファリングしてＨＤにアクセスする方法が最適と考えられます。
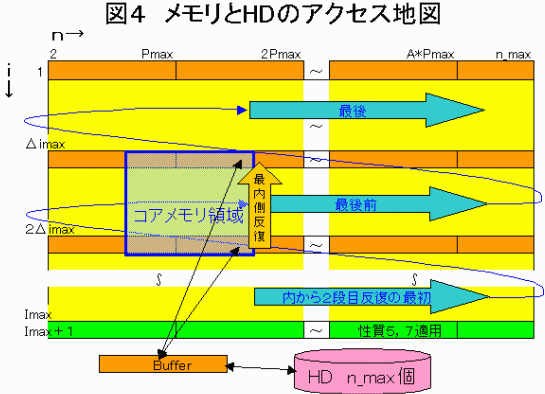
もう一つの問題はλが２００００桁にもなることです。
桁の点からも、計算時間の点からもlog(λ)で扱う必要があります。
倍精度浮動小数点(double)では１５桁が保証精度です。
まずlog(λ)そのものはlog(素数)の足し算だけですから、１５桁精度が維持されます。
問題は２つのlog(λ)を比較するとき、その差が１５桁以内かどうかです。
差は確率的には大部分 １＋log10(n1.5) 程度と推定され、
実際ｎ＝１０6まででチェックしたところ結果に影響する差は１０桁目が最小でした。
従って、ｎ＝１０8の場合１３桁で問題ないレベルです。
もちろん証明されていないので、探索の中にチェックを入れました｡
なおこの方法では、λの値やMなど幾つかの代表値を得ることは可能ですが、ｎの分割の詳細情報は失われ、再現できません。
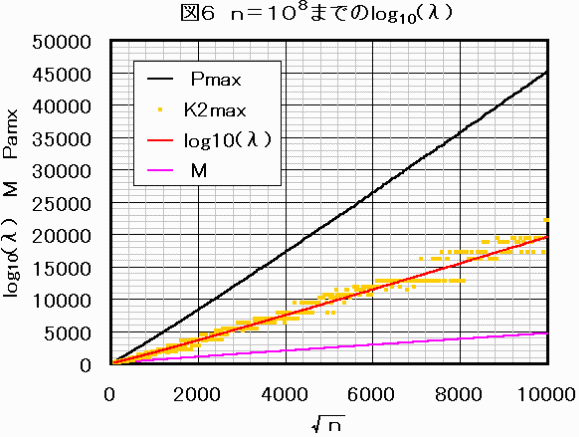
以上の方法でｎ＝１０8までの探索を行いました。
桁落ち誤差の問題は予測どおり発生せず、計算時間**は約７０時間でした。
K2maxの予測も最大64%Pmax程度で反例はありませんでした。
（**Cpu P.III 500MHz CoreMom.=128MB usedHD=1.6GB）
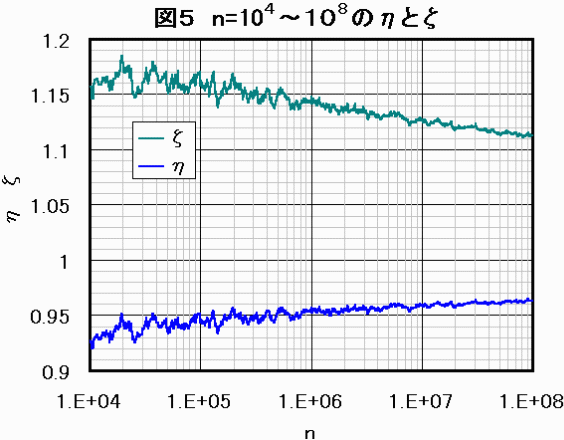
図６に計算結果を示します。
また、図５にηの状況をζとともに示します。
ηの収束に関して見込みはありそうです。
なお、ここでのη,ζはローカルに計算したもので、グローバルにチューニングした３章のη,ζとは若干ずれています。
【P.S.】
問題が漠然としていることをいい事に、本題／数学的厳密性から離れて、 プログラミング／実用性に興味が走ってしまいました。