◆静岡県の中学校2年生 紅林 麻衣さんからの解答。
どんな2桁の数でもいつか4になり、偶数なので2で割り2になり、また偶数なので2で割り、1になる。
そして、1は奇数なので、3倍して1を加えると、また4になり、どの2桁の数でも、最後は、4,2,1のくり返しとなる。
【コメント】
すばらしい分析ですね。
もちろん正解です。
どんな数でも、必ず4,2,1の繰り返しのパターンになってしまう(たぶん?)のが不思議です。
いつかすばらしいアイディアで証明する人があらわれることを期待しています。
◆神奈川県 あどるさんからの解答。
・n=3のとき
3→10→5→16→8→4→2→1→4→2→1→…
・n=7のとき
7→22→11→34→17→52→26→13→40→20→10→…
以下、n=3の時と、同じ。
・n=9のとき
9→28→14→7→…
以下n=7の時と同じ。
このように、どのようなnについても、最終的には4→2→1→4→…というループに行き着くように見える。
また、小さい方からしらみつぶしに探査していくのであれば、最初の例で見たように、中間結果がnより小さくなった時点で終了していいことになる。
まずnが偶数の時は調べなくてよい。
(nが偶数の場合、次にn=n/2となるが、これはnより小さい。)
これだけでも、調べる対象が半分になる。
なおかつ、4n+1の形の奇数について考えてみると、
これは奇数だから、次に3をかけて、1を足すことになる。
3×(4n+1)+1=12n+4=4(3n+1)
これは偶数であり、2で2回割れて、
4(3n+1)⇒2(3n+1)⇒3n+1
これは、 3n+1<4n+1
であるから、4n+1の形の奇数も探査対象からはずしてよい。
これで、全ての数を探さなくても、たった、25%の数に減ったことになる。
これで、随分楽になったはずなんですが・・・。
【コメント】
あと残るは4n+3の形の奇数ですね。
最もそこがどうしようもないのでしょうが・・・。
◆石川県 水川海之助さんからの解答。
まず、2nの場合、成り立つことは明らかである。(nは0と自然数)
次に2nの数から1を引くと3で割りきれる数を調べる。
その数は4nとなるから(証明いります?)、
|
4n−1 ―――――― 3 |
| また、 |
4n−1 ―――――― 3 |
| ここで |
4n−1 ―――――― 3 |
以上のことから、6x−3(xは自然数)という3の奇倍数が証明されれば、すべての自然数が証明できることが予想できる。
◆宮城県 斉藤 誠さんからの解答。
問題の手順から偶数を除いた数列を考えます。
ある奇数Pからコラッツの手順で生成される最初の奇数をKとする。
すると4P+1という奇数も同じ手順でKになる。
また、この4P+1の4倍+1も同じでKになる。さらにその次も。
これを
K ← P、4P+1、16P+5、・・・・・・・・(1)
と表す。
実際にK=1、5、7、・・・・・・(3の倍数を除く奇数)をあてはめると
K1= 1 ← {p1:p1=1、 5、21、・・・・・・}
K2= 5 ← {p2:p2=3、13、53、・・・・・・}
K3= 7 ← {p3:p3=9、37、149、・・・・・}
K4=11 ← {p4:p4=7、29、117、・・・・・}
・
・
・
となります。
ここで右辺の集合p1〜p∞を集めると重複しない全ての奇数の集合になります。
第1行目で明らかなように、1は1になりループになります。
{5、21、・・・・}も1のループに到達します。
第2行目{p2:3、13、53・・・}からも5を経由して1に到達する。
第3行目p2からは、7、11、17、13、5、1となる(この表では表されていませんが)
この表はEXCELなどの表計算ソフトで簡単に作成出来ます。
65535×2程度までは。
P=27から始めると41回も対応表を探さなければなりません。
電卓が早いです。
(また、右辺の第1行目をキーにしてソートしておくといいです。)
ただし、逆にたどる時は便利です。
(電卓でも出来ますが・・・プログラム電卓が必要?)
ここで数の小さい順に調べていくことを考えると、自身より小さい数は調査済みなので、右辺2列目以降は明らかに1回の操作で小さくなっています。
よって4N+1(Nは自然数)は調査対象からはずされる。
6N+5の数字は調査済みの数から生成されるコラッツ数列で通過済みなのではずす。
4N+3の数字(たとえば7)は表より順方向、逆方向どちらも大きな数字になっているものが多い。
よく調べると48で割ったあまりが、7、15、27、39、43が両方向で大きくなっていたり、3の倍数になっているので調査対象とする。
等々、調査対象を選択する方法が表から検討出来る。
ところで、水川さんの6N+3についてですが、(1)で分かるように、P、4P+1、16P+5の3数は同じKになりますがこの3数のうち1つは3の倍数です。
従って6N+3でコラッツの予想が成立すれば証明がされたことになると思います。
なお、0を除く負整数でも上記関係は成り立ちます。
負整数では、3つのループが確認されています。
(−1、−3)
(−5、−7)
(−17、−25、−37、−55、−41、−61、−91)
また、コラッツの予想を逆にたどった場合複数の数に射影されていきますので樹形図になります。
その各先端は3の奇倍数です。(偶数を除いた場合)
ただし、ループを根にします。(樹形図と呼べるかどうか疑問ですが)
一度ループから抜けて樹形図をたどり始めると2度とループにはなりません。
したがって、コラッツ予想(角谷の予想ともいうそうです)を整数に拡大すると
「0を除く整数を偶数は2で割り、奇数は3倍して1を加える」を繰り返すとついには4つの(現在知られている)ループに到達する
と言えそうです。
小谷研究室のホームページでは、正数では4000兆超まで確認されているようだ。
◆神奈川県 三島 久典さんからのコメント。
あどるさんのようなことは、以前私も考えました。
詳細はこちらに記しています。
しかし、今回、再考してみて、以下のことに気が付きました。
というのは、
an+b
ただし、
aは2のベキ乗、bはa−1
の場合は、簡略化することができない
ということです。
つまり、上記アプローチで、探査範囲をしぼりこんでいくことはできますが、必ず、解決できない部分が残ります。
要するに、このアプローチでは、この問題の解決に至ることはできません。
これこそが、この問題が難問である所以であり、
Erdosをして、
「数学はこのような問題を解くには、まったく適していない」
と言わしめた、最大の理由です。
◆宮城県 斉藤 誠さんからの解答。
この問題は自然数では全てが「最後は1−4−2−1のループになる」予想なので反例を考えます。
反例が無いことを証明すればいいと思う。
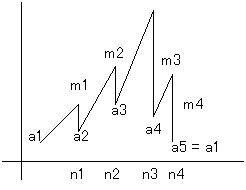
図は奇数a1から始めたコラッツマップで、n1〜n4までの4回でループになる場合を想定します。
a2〜a5はそのときに通過する奇数です。
また、m1〜m4は奇数になるように割る数=2m1等を表します。
各ステップを計算すると
| a2= | 3a1+1 ―――――――― 2m1 |
| a3= | 3a2+1 ―――――――― 2m2 |
| a4= | 3a3+1 ―――――――― 2m3 |
| a5= | 3a4+1 ―――――――― 2m4 |
|
(3a1+1)(3a2+1)(3a3+1)(3a4+1) ――――――――――――― a1×a2×a3×a4 | = 2m1×2m2×2m3×2m4 = 2p |
ここで p=m1+m2+m3+m4ですがその値は不定です。
m1などはa1によって一意に決まる値ですが簡単な関係式はみつかりません。
たとえば(a1:m1)を表すのにnを自然数とすると
(8n+1:2),(8n+3:1),(8n+5:m),(8n+7:1)です。
この(8n+5)がこの問題を難しくしている元凶のようです。
5、53、149、725など。
この関係式(1)が成り立つ整数の組み合わせを探すのですが、簡単に見つかりません。
組み合わせはこの考え方を拡張し2組〜無限組まで考えなければなりません。
コンピュータで探すしかありませんが、組み合わせが多いので何年かかるか検討もつきません。
pの値が不定ですので2の累乗数になれば成立としますが、成立する組み合わせが見つかっても本当にループになるかは実際に試す必要があります。
ただ、実際にループになればコラッツ予想の反例となることはもちろんです。
成立する組み合わせは負数もいれて
(a1、a2)=(1,1),(−5,−7)など4例あります。
これは確認するだけなので簡単です。
この4例以外に無いとなると・・・・・・・・
「方程式は出来たけど難しさはさらに増してしまった」
◆石川県 水川海之助さんからの解答。
『コラッツの定理』の証明範囲が6n−3となるための証明
任意の自然数n0において2n0−1として任意の奇数を表すこととする。
『コラッツの定理』において奇数は3倍して1を加えるから
3×(2×n0−1)+1
=6×n0−2
=2×(3×n0−1)
つまり、6×n0−2は偶数でかつ3で割ると1あまる数、または6で割ると4あまる数であることが判る。
(1(mod3)かつ0(mod2))
一方、任意の自然数n1-1、n1-0、n1-2を使って、3で割ると1あまる奇数、3の奇倍数、3で割ると2あまる奇数を表すと、
6×(n1−1)−5
6×(n1−0)−3
6×(n1−2)−1
となり、6×(n1−1)−5,6×(n1−2)−1をそれぞれ4倍、2倍すると
4×(6×(n1−1)−5)
=24×(n1−1)−20
=3×(8×(n1−1)−7)+1
2×(6×(n1−2)−1)
=12×(n1−2)−2
=3×(4×(n1−2)−1)+1
とそれぞれ3で割ると1あまる偶数となる。
1(mod3)かつ0(mod2)
6×n0−2,24×(n1−1)−20,12×(n1−2)−2はそれぞれ3で割ると1あまる偶数であるから、
6×n0−2=12×(n1−2)−2
6×n0−2=24×(n1−1)−20 と置くと
n0=2×(n1−2)
n0=4×(n1−1)−3
となり、n0全体の3/4において任意の奇数2×n0−1において3倍して1を加えた後奇数になるまで2で割り続けると、3で割ると1あまる奇数、または3で割ると2あまる奇数にたどり着くことが判る。
ここで残ったn0全体の1/4をn0=4×n1−1と置く。
(n1は自然数)
一方、3で割ると1あまる偶数に4をかけると、任意の自然数mとおいて
4×(6×m−2)
=24×m−8
=3×(8×m−3)+1
=2×(12×m−4)
とやはり3で割ると1あまる偶数となるので、
任意の自然数n2−1、n2−0、n2−2とおいて
6×(n2−1)−5
6×(n2−0)−3
6×(n2−2)−1を表して
4×4×(6×(n2−1)−5)=96×(n2−1)−80
4×2×(6×(n2−2)−1)=48×(n2−2)−8
また、2×(4×n1−1)−1=8×n1−3において
3×(8×n1−3)+1=24×n1−8
これらは、それぞれ3で割ると1あまる偶数だから、
24×n1−8=48×(n2−2)−8
24×n1−8=96×(n2−1)−80 と置くと
n1=2×(n2−2)
n1=4×(n2−1)−3
となる。
この作業を無限回繰り返すと『コラッツの定理』によって
2×n0−1のうちの2/3が3で割ると2あまる奇数へたどり着き、残り1/3が3で割ると1あまる奇数へたどり着くことになる。
よって、すべての奇数2n−1において3倍して1加えたものを奇数になるまで2で割っていくと3で割ると2あまる奇数かあるいは3で割ると1あまる奇数にたどり着くことが判る。
よってコラッツの定理の証明範囲が3の奇倍数であることが判る。