◆静岡県 ヨッシーさんからの解答。
【問題１】
まず思いついたのが、
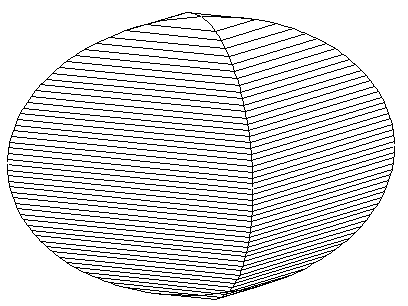
『直径ａの円柱を交わらせたときの共通部分』です（図参照）。
でも、この場合、平面図に線がついてしまいます。
他に思いつかないので、このまま体積を求めます（強引な）。
【問題２】
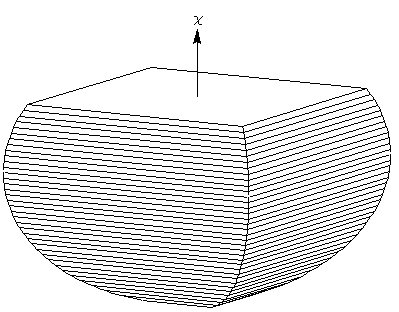
図のように、ｘ軸をとり、ｘ軸に垂直な面でこの立体を切ると、正方形になります。
| これを - | a 2 |
〜 | a 2 |
まで積分します。 |
| 簡単のため、b= | a 2 |
と置きます。 |
切り口の正方形の１辺の長さは
ですから、
面積は、４（ｂ2−ｘ2）です。
よって、
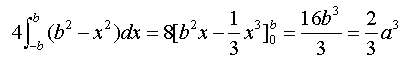
| 答え | ２ ３ | ａ3 |
式の羅列じゃないということは、やっぱり間違ってるのかなぁ。
【コメント】
ここはやっぱりＧＯＦＹ・和人 さんにコメントをお願いしましょう。
ＧＯＦＹさん、飲んでいる場合じゃないですよ。
【ＧＯＦＹ・和人 さんからのコメント】
問１コメント：
平面図に線・・確かにヨッシーさんのご指摘、正しいのら。
平面図の真ん中あたりは、ぼんやりするんらけれろ。
線を入れると形がバレちゃうからズルしたのらよ。ごみんなさい。
ヨッシーさん、強引ではなく、あんたわ正しい！
問２コメント：
数式のろれつが回らない？？
ろれつはどうでもいいんら。
んねぇ、こんな問題があったれひょ、
「与えられた円とおにゃじ面積の正方形を定規とコンパシュで描け」
この問題・・たひか「将棋とコンパスでπを求めよ」に還元しゅるんだにょな。
文字通り無理数だんね。
◆東京都 eikiさんからの解答。
【速報】として答えます。
形は、直交する水道管の共通部分、あるいは、空缶に詰めて固めた土を取り出して、横から空缶で切る、といった感じ。
体積は。。。
球を薄くスライスした微小高さの円柱で積分したものと考え、この立体は薄くスライスした微小高さの正４角柱で積分したものと考えると
球：この立体＝π：４になるはず。
| したがって | ２ ３ | ａ3 |
どちらも検証していないので、検証できたら【確報】として送るつもりです。
◆東京都 eikiさんからの解答。
【確報】です。
微小高さの円柱（正４角柱）を中心角の関数と見て３角関数で積分しようと苦労していたのですが、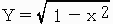
より底面積を計算すれば簡単に積分できました。
円柱の底面積 ＝π×Ｙ2
正４角柱の底面積 ＝ ４×Ｙ2
したがって、球の体積：この立体の体積 ＝π：４ だから
| 球の体積 ＝ | ４ ３ | π×半径3より |
| １６ ３ | ×半径3となります。 |
| この立体の半径は | ａ ２ | なので、 |
| 答は | ２ ３ | ａ3 |
【コメント】
ようやく確認できました。
間違いなく正解です。
おまけですが、直径ａの円柱３つが直角に交わった場合の共通部分の体積も計算できます。
関心のある方は挑戦してみてください。
◆岐阜県 水の流れさんからの解答。
| 直交する半径ａの３つの直円柱の共通部分の体積を求めよ。
不等式で表すと、 |
解答
立体Ｔの概形がわからなくとも、平面スライス形により求めてみる。
ＴをＺ＝ｋ（一定）の平面で切った切り口はｚの値によって形が異なる。
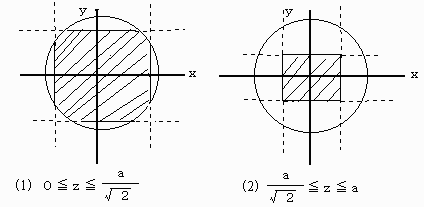
＜参考＞
立体Ｔのモデルは大きな消しゴムを円柱状の型で真上・真横・真正面の３方向から切断すると良い。
＊連想としては「栗」がよいかも。
ｘ≧０，ｙ≧０，ｚ≧０ で書いてみます。
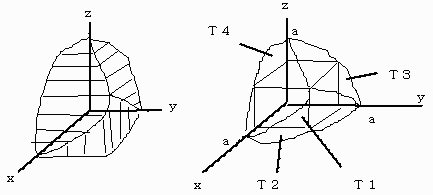
立体Ｔ１、Ｔ２の体積を、それぞれＶ１，Ｖ２とする。
立体Ｔの体積をＶとすると、
| Ｖ ８ |
＝Ｖ１＋３Ｖ２ ・・・ （＊）である。 |
| そこで、立体Ｔ１は１辺の長さが | ａ |
の立方体だから、 |
| その体積Ｖ１は、Ｖ１＝（ | ａ |
） | 3 |
| Ｖ１＝ | ａ3 ４ | ・・・(1) |
| また、立体Ｔ２を平面ｘ＝ｋ（ | ａ |
≦ｋ≦ａ） |
Ｓ(ｋ)＝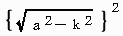
＝ ａ2−ｋ2
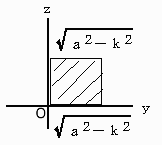
よって、立体Ｔ２の体積Ｖ２は
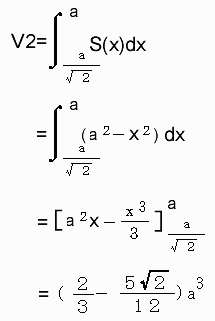
以上より、求める体積Ｖは、(1)、(2)を（＊）に代入して、
| Ｖ ８ |
＝Ｖ１＋３Ｖ２ |
| ＝ | ａ3 ４ |
＋３( | ２ ３ |
− | ５ １２ |
ａ3 | ) |
| ＝(２−)ａ3 |
∴Ｖ＝８（２− ）ａ3 ・・・（答え）