亀儅儔僜儞戝夛亁夝摎
仧嶳棞導丂傕偭偪 偝傫偐傜偺夝摎丅
巹偼昁偢懚嵼偡傞偲偄偊傞偲巚偄傑偡丅
傑偢丄俙孨偺暯嬒偼丄俁暘偱侾倠倣憱傞偙偲偑偱偒傑偡丅
偨偩偟丄俙孨偼俁暘偁偨傝偵侾倠倣偺懍搙偱忢偵憱偭偰偄傞偲偼偄偊傑偣傫丅
偟偐偟丄暯嬒偲偄偆偙偲偼丄偙偺俁暘偁偨傝侾倠倣傛傝懍偄偲偒傕偁傟偽丄抶偄偲偒傕偁傞偲偄偆偙偲偱偡丅
乮徹柧乯
俙孨偑弌敪偟偨偁偲丄俁暘屻偵俁暘慜偺俙孨偲慡偔摨偠摦偒傪偡傞僑乕僗僩俙孨偑弌敪偡傞偲偟傑偡丅
俙孨偲偺嵎偼昁偢俁暘側偺偱丄慡偰偺応崌偵偍偄偰丄偙偺俀恖偺嫍棧偑侾倠倣偵側傟偽丄戣堄偼惉傝棫偮偲偄偊傑偡丅
鶣乯
俙孨偑巒傔丄俁暘侾倠倣埲壓偺懍搙偱憱偭偰偄偨偲偒丄僑乕僗僩俙孨偲偺嫍棧偼侾倠倣埲壓偱偡偑丄偳偙偐偱儁乕僗傪偁偘側偄偲丄僑乕儖偵娫偵崌偄傑偣傫丅
儁乕僗傪俁暘侾倠倣埲忋偵偁偘側偄偲側傜側偄偺偱丄偦偆偡傞偲丄僑乕僗僩俙孨偲偺嫍棧偑侾倠倣埲忋偵側傝傑偡丅
嫍棧偑棧傟傞偲偒偵丄堦弖偱傕昁偢俀恖乮丠乯偺嫍棧偑侾倠倣偵側傞偲偒偑偁傝傑偡丅
偦偆側傜側偄偨傔偵偼丄弖娫堏摦偟偐偁傝傑偣傫偺偱丄暔棟揑偵偁傝摼傑偣傫丅
鶤乯
俙孨偑巒傔丄俁暘侾倠倣埲忋偺懍搙偱憱偭偰偄偨偲偒丄僑乕僗僩俙孨偲偺嫍棧偼侾倠倣埲忋偁傝傑偡丅
偙偺傑傑僑乕儖偱偒傟偽椙偄偺偱偡偑丄俆倠倣傪侾俆暘偲偄偆偙偲側偺偱丄偳偙偐偱儁乕僗傪棊偲偡偐巭傑傞偐偟側偔偰偼側傝傑偣傫丅
儁乕僗傪棊偲偡丄傑偨偼巭傑偭偰偟傑偊偽帺暘偲慡偔摨偠摦偒傪偡傞僑乕僗僩俙孨偱偡偐傜丄堦弖偱傕俁暘侾倠倣埲壓偵側傠偆傕偺側傜丄俀恖偺嫍棧偑侾倠倣傪偒偭偰偟傑偄傑偡丅
偙偺侾倠倣偺嫬栚偑昁偢偁傝傑偡丅
鶥乯
俙孨偑忢偵堦掕偺儁乕僗偺偲偒丄
偙偺応崌偼丄忢偵俁暘侾倠倣偺儁乕僗側偺偱栤戣側偟丅
鶣乣鶥傛傝丄俙孨偲僑乕僗僩俙孨偺嫍棧偑侾倠倣偵側傞偲偒偑昁偢懚嵼偡傞偲偄偊傑偡丅
傛偭偰丄俁暘偪傚偆偳偱憱偭偨侾僉儘偺嬫娫偑昁偢懚嵼偡傞偲偄偊傑偡丅
仧垽抦導丂Y.M.Ojisan 偝傫偐傜偺夝摎丅
亂夝摎亃丂偄偊側偄丅
斀椺丗
乮侾乯弌抶傟偨
乮俀乯僐乕僗娫堘偊偨
乮俁乯僩僀儗偵嬱偗崬傫偩丂摍丂懍搙侽忬懺傪娷傓応崌丅
亂姶憐亃
慺捈偵峫偊偨嵟弶偼堷偭偐偐傝傑偟偨丅刅剙剛剙剨剙!
仧媨忛導丂娒愹朄巘 偝傫偐傜偺夝摎丅
斀椺
俙孨偼嶐擔丄揙栭偱僥儗價僎乕儉傪偟偰偄偨偺偱柊偔偰偨傑傜側偄丅
弌敪僎乕僩偱怮偰偟傑偄僗僞乕僩偺崌恾偵傕婥偯偐側偄丅
偼偭偲栚偑偝傔偨傜傕偆弌敪偺崌恾偐傜侾係暘偨偭偰偄偨丅
俙孨偼偁傢偰偰僗僞乕僩偟偰挻恖揑側憱傝偱俆僉儘傪侾暘偱憱攋偟偨丅
仧搶嫗搒偺崅峑惗丂MATIX 偝傫偐傜偺夝摎丅
仧垽抦導丂Y.M.Ojisan 偝傫偐傜偺夝摎丅
仧媨忛導丂娒愹朄巘 偝傫偐傜偺夝摎丅
偙傟偵懳偟偰斀榑
懍搙侽忬懺傪娷傓応崌丅
偙傟偼丄師偺偙偲偑峫偊傜傟傑偡丅
侽亝倲亝侾係偺偲偒丄倴亖侽(km/h)
侾係亝倲亝侾俆偺偲偒丄倴亖俁侽侽(km/h)
偁傝偊側偦偆偱偡偑丄偙偺偲偒丄侾係暘侾俀昩偺偲偒丄侾僉儘抧揰傪捠夁偟傑偡丅
偮傑傝丄侾侾暘侾俀昩偐傜丄侾係暘侾俀昩偵偐偗偰丄侾僉儘憱偭偨偙偲偵側傝傑偡丅
偙偙偱丄偙偺栤戣偺庯巪傪峫偊偨偄偲巚偄傑偡丅
倲暘屻偵偄傞抧揰傪倖(倲)倠倣偲偍偒傑偟傚偆丅
偙偺栤戣偱偼丄俁暘娫偱憱偭偨嫍棧偑侾僉儘偵側傞偙偲偑偁傞偐偳偆偐側偺偱丄
丂丂倖(倲亄俁)亅倖(倲)亖侾丂丂(侽亝倲亝侾俀)
傪枮偨偡倲偑懚嵼偡傞偐偱偡丅
偙偙偱丄尰戙偺幮夛偵偍偄偰丄儚乕僾偼巊偊傑偣傫丅(偙傟廳梫丅)
偮傑傝丄倖(倲)偼楢懕側偺偱偡丅
偙偙偱丄倖(倲)偺抣偵偮偄偰偱偡偑丄僗僞乕僩抧揰傛傝慜偺傎偆偵憱偭偨偲偐僑乕儖傪捠夁偟偨偲偄偆偙偲偑
側偄傕偺偲偟偰峫偊傞偲丄
丂丂侽亝倖(倲)亝侾俆
偲側傝傑偡丅
偙偙偱丄俥(倲)亖倖(倲亄俁)亅倖(倲)丂丂丂(侽亝倲亝侾俀)
偲掕媊偡傞偲丄
丂丂亅侾俆亝俥(倲)亝侾俆丂丂(侽亝倲亝侾俀)
偲側傞偱偟傚偆丅(庒姳暆偼峀偔偟偰偄傑偡丅)
俥(倲)偼楢懕偩偐傜丄乮倖(倲)偼楢懕側偺偱丅乯
俥(倲)亖侾丂侽亝倲亝侾俀丂傪枮偨偡倲丂偑懚嵼偡傞丅
偮傑傝丄俁暘偪傚偆偳偱憱偭偨侾僉儘偺嬫娫偑昁偢懚嵼偡傞偲偄偊傞丅
偨偩偟丄偙偙偱丄儚乕僾偲偄偆傕偺偑側偄丄尰戙幮夛偺応崌偱偁傞偙偲偵拲堄偟偰傎偟偄丅
仧搶嫗搒偺拞妛峑俀擭惗丂惵偺僩儔儞僾 偝傫偐傜偺夝摎丅
懍搙侽傪娷傫偱偄偨偲偟偰傕戝忎晇偩偲巚偄傑偡丅
俙孨偑偁傢偰偰僗僞乕僩偟偰挻恖揑側憱傝偱俆僉儘傪侾暘偱憱攋偟偨偲偟偰傕
憱傝巒傔偰偐傜侾侾暘侾俀昩屻偐傜侾係暘侾俀昩屻傑偱偺俁暘娫偵侾僉儘偪傚偆偳憱偭偰偄傑偡丅
偟偐偟搑拞偱堷偒曉偟偨傝偡傞偲榖偼暿偵側傞偲巚偄傑偡丅
偮傑傝憱偭偨嫍棧偺崌寁偑俆僉儘傪挻偊偨応崌偼斀椺偑敪惗偟傑偡丅
斀椺
忢偵侾暘侾僉儘偺懍偝偱憱傝懕偗僑乕儖偑嬤偔側偭偨傜偦偺偁偨傝傪摨偠懍偝偺傑傑偆傠偆傠
偟偰侾俆暘偨偭偨帪偵僑乕儖偡傞丅
仧嶳棞導丂Footmark 偝傫偐傜偺夝摎丅
亂摎偊亃
偄偊傑偡丅
亂徹柧亃
憱峴嫍棧X噏偐傜X亄侾噏傑偱偵梫偡傞帪娫傪F(X)偲偡傞偲丄
娭悢F(X)偼侽亝X亝係偵偍偄偰楢懕偱偡丅
仠丂F(侽),F(侾),F(俀),F(俁),F(係)偺偳傟偐偑俁偺偲偒
柧傜偐偵丄俁暘偪傚偆偳偱憱偭偨侾僉儘偺嬫娫偼懚嵼偟傑偡丅
仠丂F(侽),F(侾),F(俀),F(俁),F(係)偺偳傟傕俁偱側偄偲偒
F(侽)亄F(侾)亄F(俀)亄F(俁)亄F(係)亖侾俆 傛傝丄
F(侽),F(侾),F(俀),F(俁),F(係)偺偳傟傕俁枹枮偱偁傞偙偲偼偁傝摼傑偣傫丅
偦傟屘丄俆偮偺撪偺彮側偔偲傕侾偮偼俁傛傝戝偒偄敜偱偡丅
摨條偵丄F(侽),F(侾),F(俀),F(俁),F(係)偺偳傟傕俁傛傝戝偒偄偙偲傕偁傝摼傑偣傫丅
偦傟屘丄俆偮偺撪偺彮側偔偲傕侾偮偼俁枹枮偺敜偱偡丅
偱偡偐傜丄F(倫)亙俁亙F(倯)偲側傞倫偲倯偑昁偢懚嵼偟傑偡丅
乮偨偩偟丄倫,倯偼倫,倯伕(侽,侾,俀,俁,係)偱偡丅)
傛偭偰丄拞娫抣偺掕棟傛傝F(倰)亖俁偲側傞倰偑昁偢懚嵼偡傞敜偱偡丅
乮偨偩偟丄倫亙倰亙倯 傑偨偼 倫亜倰亜倯乯
徹柧偼廔傢傝偱偡丅
仧嶳棞導丂Footmark 偝傫偐傜偺僐儊儞僩丅
乽憱偭偨嫍棧偼俆僉儘丄僞僀儉偼侾俆暘偱偟偨丅乿偑丄尩枾偝偵庒姳寚偗傞偨傔丄
A孨偼乽侾俆暘娫偱俆僉儘憱偭偨乿偁傞偄偼乽侾俆暘娫偱弌敪抧揰偐傜僐乕僗忋俆僉儘愭偵偁傞抧揰偵摓拝偟偨乿
偺俀捠傝偺夝庍偑懚嵼偟傑偡丅
慜幰偺偽偁偄丄壖偵僐乕僗偵娭學側偄偲偙傠傪帺桼偵憱偭偨偲偟偰傕丄柧傜偐偵俁暘偪傚偆偳偱憱偭偨侾僉儘偑懚嵼偟傑偡丅
屻幰偺偽偁偄丄僐乕僗傪媡栠傝偡傞偺偑惵偺僩儔儞僾偝傫偺斀椺偱偡偑丄侾俆暘娫偼僐乕僗忋偵偄傞偺偱傗偼傝楢懕偱偡丅
偡傞偲丄弌敪抧揰偐傜僐乕僗忋傪嵟弶偵X僉儘恑傫偩偲偒偐傜丄僐乕僗忋傪偝傜偵侾僉儘愭偵恑傫偩抧揰偵嵟弶偵偄傞偲偒傑偱偺帪娫傪丄巹偑愭偺夝摎偱帵偟偨F(X)偲峫偊傟偽丄
傗偼傝丂F(侽)亄F侾亄F俀亄F俁亄F係亖侾俆 偑惉棫偟傑偡丅
傛偭偰丄拞娫抣偺掕棟偑摨條偵惉棫偟丄僐乕僗傪媡栠傝偟偰傕忢偵僐乕僗忋偵偄傞偺側傜斀椺偵偼側傝傑偣傫丅
偮傑傝丄侾俆暘娫偡傋偰偵僐乕僗忋偺懍搙偑懚嵼偡傞偺側傜丄懍搙偑儅僀僫僗傕懍搙偑侽摨條偵斀椺偵側傝傑偣傫丅
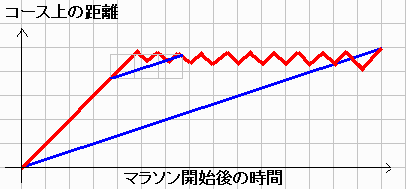
嫮偄偰斀椺傪偁偘傞側傜丄屻幰偺夝庍偱僐乕僗埲奜偱帪娫傪旓傗偟偨偲偒偱偡丅
偙偺偲偒丄偦偺帪娫偼僐乕僗忋偺懍搙偼懚嵼偟傑偣傫偐傜丄僌儔僼偼偦偺帪娫偺暘偑柧傜偐偵徚偊楢懕偱偼偁傝傑偣傫丅
偱偡偐傜丄嵟弶偺俀暘俁侽昩偱僐乕僗傪俀丏俆僉儘憱傝丄偦偙偱僐乕僗偐傜奜傟偨偲偙傠傪偖傞傝偲侾侽暘娫憱傝丄
儅儔僜儞奐巒偐傜侾俀暘俁侽昩屻偵僐乕僗偵栠傝丄巆傝敿暘偺俀丏俆僉儘傪俀暘俁侽昩偱憱傞偺偼斀椺偵側傝傑偡丅
側偤側傜丄乽俁暘偪傚偆偳偱憱偭偨侾僉儘偺嬫娫偑昁偢懚嵼偡傞偲偄偊傞偱偟傚偆偐丠乿偲尵傢傟偰傕丄僐乕僗傪憱偭偨楢懕俁暘娫偼懚嵼偟傑偣傫丅
仧垽抦導丂Y.M.Ojisan 偝傫偐傜偺僐儊儞僩丅
x=f(t) 傪梡偄傞偲 f伕侽媺楢懕娭悢on[0,15] 側偺偱丂妋偐偵倄俤俽偱偡丅
偱傕t=g(x)傪梡偄偨応崌偼g偼 g伕楢懕娭悢 偲偼尷傜側偄偺偱俶俷偺応崌偑偁傝傑偡丅
偮傑傝栤戣暥偵偍偄偰侾倠倣偺嬫娫偑偁傞偐偲栤偆偰偄傞偺偱俶俷偱偡丅
傕偟侾倠倣堏摦偡傞俁暘娫偑偁傞偐偲栤傢傟傟偽倄俤俽偱偡丅
丂傕偭偲傕丄巭傑偭偨倶抧揰偺捠夁帪娫偺婰榐傪椺偊偽侾侾暘偐傜侾俀暘偺慡偰偲峫偊傞応崌偼暿偱偡丅
偙偆側傞偲儔僢僾僞僀儉偺掕媊偺栤戣偱偡丅
偦偺応崌丄栤戣偺侾倠倣偵懳偟偰暋悢偺憱峴帪娫偑懚嵼偡傞偺偱丂乽俁暘偪傚偆偳乿偲偄偆偺偑揔摉側昞尰偐丄傗偼傝堷偭偐偐傝傑偡丅
丂亀儅儔僜儞戝夛亁傊
丂悢妛偺晹壆傊傕偳傞
