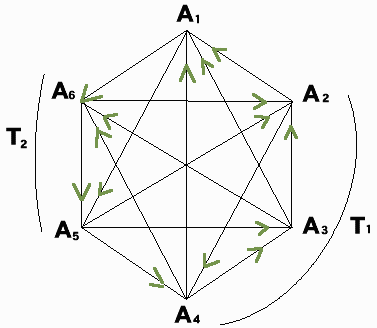
 n=6のときの例です。
n=6のときの例です。◆茨城県 内桶 次郎さんからの解答。
リーグ戦に参加したチームの数nが偶数か奇数かで場合分けをする。
また、以下のような記号を使用する。
・参加チームをA,B,C・・・、A1,A2,A3,・・・An等で表し、
W(A)でAが勝った相手チームの総数を表す。
・またいくつかのチームの集合をT1,T2等で表し、
|T1|でそのT1に属するチームの数を表すことにする。
《case1》
参加チーム数nが偶数のとき、つまりn=2kのとき(k=1,2,3,4・・)、
参加チームをA1,A2,A3,・・・Anとする。
このときリーグ戦で行われる試合の総数は、
| 2kC2= | 2k(2k−1) ―――――――― 2 | =k(2k−1) |
| つまり、 | 2k Σ i=1 | W(Ai)=k(2k−1)・・(1) |
さて、ここで一般性を失うことなく優勝チームをA1としてよい。
優勝チームA1は他のチームと同じ勝利数かそれ以上の勝利数を獲得しているはずなので、任意のチームAiについて、
W(Ai)≦W(A1)が成立する。・・(2)(i=1,2,3・・、2k)
ここでW(A1)=a1とすると、
a1≧kが成立する。・・(3)
|
◆(3)が成立する理由
仮にa1<kとすると、a1≦k−1となる。
2k(k−1)<k(2k−1)なので、
となり、これは(1)に矛盾する。 ∴(3)が成立する。 (この証明は本質的に「鳩の巣箱の原理」である。) |
ところで(3)は優勝チームは必ずk試合以上勝っていることを示している。
さて、ここで優勝チームA1が勝利した相手チームの集合を、T1とする。
またA1が負けた相手チームの集合を、T2とする。
(3)より|T1|=W(A1)=a1≧k・・(6)
|T2|=n−1−a1≦k−1・・(7)
明らかにB∈T1のときはA1>Bとなる。・・(ア)
(>の定義1より)
またC∈T2のときもA1>Cとなる。・・(イ)
(T2=φのときは(ア)のみが成立するのでT2≠φとしてよい)
|
◆(イ)が成立する理由
T2の任意のチームをCとする。
なぜならば仮にCがT1の各チームの全てに勝利しているとすると・・(10)
よって(9)が成立することになります。 またこのBはB∈T1なので(A1に負けているので) A1>B・・(12) そこで(11),(12)からA1>Cが成立する。 (イ)が証明できました。 |
(ア)、(イ)より優勝チームA1についてはA1以外の任意のチームBについて、
A1>Bが成立することが証明できました。
【蛇足1】
A>Bであることを点Bから点Aに向かう矢線 B→A で表すことにすると、以上の関係は次の図のように図式化できます。
 n=6のときの例です。
n=6のときの例です。
この図の中ではA1,A2,A6が3勝2敗で3チームが優勝しています。
A3,A4,A5が2勝3敗です。
また試合総数は
| 6C2= | 6・5 ――――――― 2・1 | =15試合 |
《case2》
参加チーム数nが奇数のとき、つまりn=2k+1のとき(k=1,2,3,・・)、
参加チームをA1,A2,A3,・・・Anとする。
このときリーグ戦で行われる試合の総数は、
| 2k+1C2= | (2k+1)2k ―――――――― 2 | =k(2k+1) |
| 2k+1 Σ i=1 | W(Ai)=k(2k+1)・・(1) |
さて、ここで一般性を失うことなく優勝チームをA1としてよい。
このA1については任意のチームAiについて、
W(Ai)≦W(A1)が成立する。・・(2)(i=1,2,3・・)
ここでW(A1)=a1とすると、
a1≧k・・(3)が成立することになります。
|
◆(3)が成立する理由
仮にW(A1)=a1<kとすると、a1≦k−1となる。 W(Ai)≦W(A1)=a1≦k−1・・(4)となる。 (4)より
(2k+1)(k−1)<k(2k+1)なので、
となり、これは(1)に矛盾する。 ∴(3)が成立する。 (この証明は本質的に「鳩の巣箱の原理」である。) |
ところで(3)は優勝チームの勝った相手チーム数がkチーム以上であることを主張しています。
さて、ここで優勝チームA1が勝利した相手チームの集合を、T1とする。
またA1が負けた相手チームの集合を、T2とする。
(3)より|T1|=W(A1)=a1≧k・・(6)
|T2|=n−1−a1≦k・・(7)
明らかにB∈T1のときはA1>Bとなる。・・(ア)
(>の定義1より)
またC∈T2のときもA1>Cとなる。・・(イ)
(T2=φのときは(ア)のみが成立するのでT2≠φとしてよい)
|
◆(イ)が成立する理由
T2の任意のチームをCとする。
なぜならば仮にCがT1の各チームの全てに勝利しているとすると・・(10)
よって(9)が成立することになります。 またこのBはB∈T1なのでA1>B・・(12) そこで(11),(12)からA1>Cが成立する。
|
(ア)、(イ)より優勝チームA1についてはA1以外の任意のチームBについて、
A1>Bが成立することが証明できました。
【蛇足2】
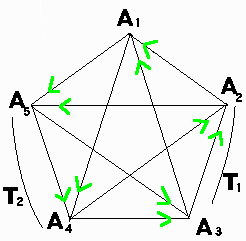 case1と同様にn=5のときの例を示しておきます。
case1と同様にn=5のときの例を示しておきます。
この結果ではA1,A2,A3,A4,A5全てが2勝2敗で全チームが優勝チームとなっています。
試合総数は
| 5C2= | 5・4 ――――――― 2・1 | =10試合です。 |
蛇足1,2のように図示したとき、
W(Ai)=点Aiを指示している矢印の本数
が成立しています。
このことからも
| n Σ i=1 | W(Ai)=nC2 |
上記の問題は
|
◆W(Ai)が最大となる点A1に対しては、他の任意の点から2ステップ以内で矢印の方向に沿って移動できる という性質と同値です。 |
◆神奈川県 飯田 孝久さんからの解答。
・優勝チームをAとする。
Aが勝利したチームBに対しては、仮定よりAはBより強いといえる。
今、Aが負けたチームをCとする。
Cが、Aが勝ったすべてのチームに勝ったとすると、Cの勝ち数がAの勝ち数を越えるため、Aが優勝したことに矛盾する。
したがって、CはAが勝ったチームのうち少なくとも一つのチーム(Dとする)には負けている。
その結果、AはDに勝ち、DがCに勝っているので、AはCより強いといえる。
よって、優勝チームは残りのすべてのチームより強い。
・付録
場合によっては、残りのすべてのチームが優勝チームより強いこともあります。
例を一つ挙げます。
優勝チームがある1チームだけに負け、そのチームが残りすべてのチームに負けた場合。
他にもあります。
【コメント】
この証明はシンプルでよいですね。これで十分です。
付録の方は、普段よく使っているような内容のこの定義が、いかにいい加減であるかのよい例になりますね。