
◆滋賀県 ippei さんからの解答。
【問題1】
3つに切断した線分の長さをa≦b≦c(a+b+c=1)とする。
| cに着目すると、c≧ | 1 3 | ,また、a+b>cであるから |
| ∴ | 1 2 | >c |
| よって | 1 2 | - | 1 3 | = | 1 6 |
| cのとりうる 値は1- | 1 3 | = | 2 3 |
| 従って、 | 1 6 | / | 2 3 | = | 1 4 |
| 答え | 1 4 |
◆愛知県 Y.M.Ojisan さんからの解答。
【問題1】
線分の長さを1とし、切断位置を0≦x,y≦1とします。
3角形になるには最大長が0.5以下であればよい。
最大長C=max(1-max(x,y),min(x,y),abs(x-y)) です。
下図はその等高線図です。
緑の3角形内がC≦0.5です。
よって確率は1/4です。
ただし確率密度f(x,y)=1とした場合です。

【PS1】
ippei さんの解答が理解できず、計算してみました。
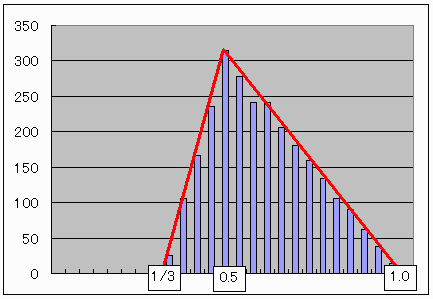
Cに対する確率密度関数は3角形が成立する限界値を頂点とする三角波でした。
下図参照。
それでCだけの考察で正解が出ることが理解できました。
【PS2】
f(x,y)=1としましたが、他の確率も考えられます。
まずxにおいて一様確率で切ります。
どちらかを1/2の確率で選びます。
選んだ方を一様確率で切ります。
即ち
| f(x,y)= | 1 2-2x |
,y≧x |
| f(x,y)= | 1 2x |
,y≦x |
これを前出の緑三角形内で積分すると
| 0.5 ∫ 0 |
x 2-2x |
dx+ | 1 ∫ 0.5 |
1-x 2x |
dx |
| = | 1 ∫ 0.5 |
1-x x |
dx |
| =ln(2)- | 1 2 | =0.193<0.25 |
【問題2】
【想定される解】
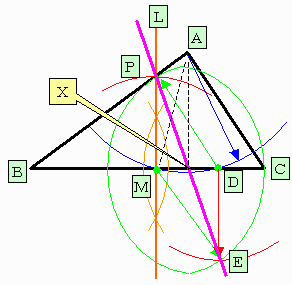
(1)斜辺BCの垂直2等分線Lを作図し、中点Mと点Pを定めます。
二等辺三角形ではないのでPとAは一致しません。
(2)AM=ADなる点DをBC上にコンパスだけで定めます。
(3)PM=DE , PD=MEなる点Eをコンパスだけで定めます。
(4)線分PE三角形面積の2分線です。
∵PEとBCの交点はMDの中点です。
従ってAのBCへの垂線の足Xです。
AMは面積2等分線です。
線Lからの距離はAもXも同じです。
【例外】
![]() BP=ABの場合、面積2等分線PEがACに平行になります。
BP=ABの場合、面積2等分線PEがACに平行になります。
従って、その場合はこの方法では描けません。
いつでも可能なチェックの方法は、ABを対角線とする、辺の長さBPのひし形の残り2頂点をコンパスで描き、その2点間がABと同じ長さであるか判定します。
同じときは、正方形なので![]() BP=ABです。
BP=ABです。
【例外に対する解】
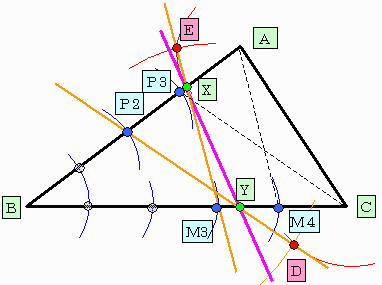
(1)斜辺BC上にBから等間隔に4点コンパスでとります。
最後の2点をM3,M4とします。
(2)同様に辺BA上にBから等間隔に3点コンパスでとります。
最後の2点をP2,P3とします。
(3)AM4に平行でM3を通る直線M3Eを書きます。
これはコンパスで平行四辺形AM4M3Eの頂点Eを定めれば作図できます。
(4)M3 EとABの交点をXとします。
| このときBX= | 3 4 |
ABです。 |
(5)CP3に平行でP2を通る直線P2Dを書きます。
これはコンパスで平行四辺形CP3P2Dの頂点Dを定めれば作図できます。
(6)P2 DとCBの交点をYとします。
| このときCY= | 2 3 |
CBです。 |
(7)XYをとおる直線XYは面積の2等分線です。
| ∵ | 3 4 | AB* | 2 3 | CB= | 1 2 | AB*CB |
【その他期待されていない解】
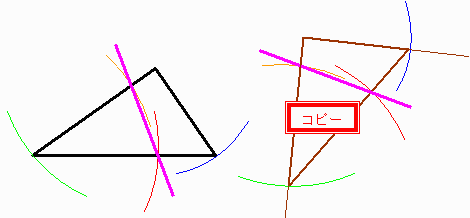
適当な直交線(茶色)を書いてその上に与えられた三角形(黒)と合同な三角形をコンパスを用いてコピーする。
コピーの上で2等分線(紫)を作図して、再びコンパスで元の図上にコピーする。
作図途中で平行になったり、頂点を通る可能性はあるが、その確率は0である。
【PS3】
【例外に対する解】は2等辺直角3角形でもOKです。
またPEがACに平行か吟味も不要です。
さらに、直角3角形であるという足かせも関係ありません。
◆神奈川県 A-Leo さんからのコメント。
【問題1について】
確率分布の取り方によって、確率が変わってしまう問題は「半径1の円に交わる直線を引く時、その直線が円で切られ
る弦の長さが![]() 以下である確率はいくらか」というBertrandの問題も有名です。
以下である確率はいくらか」というBertrandの問題も有名です。
Y.M.Ojisanさんの解を見た時、ふとそのことを思い出しました。
このように、二つ以上の確率がでてきてしまう場合、一つの解決方法としては、「ユークリッド空間の等長変換によってかわらないような確率測度(確率密度と考えていただいても結構ですが)を採用せよ」というのが積分幾何の教えるところです。
「等長変換」とは長さを変えない変換のこと、つまり、どの方向からどう見ても確率が同じようにしなさいということです。
この問題の場合、1次元のユークリッド空間で考えれば十分です。
この場合、等長変換は平行移動か対称移動の二つと、その組み合わせによって得られるもので尽くされます。
f(x,y)=1と置いた場合は平行移動をしても対称移動をしても確率密度に変化はありません。
Y.M.Ojisanさんの挙げられた確率密度の場合はちょっと複雑です。
たとえば、対称移動x,y→-x,-yという変換では、大小関係が入れ代わります。
| y≧xの場合、f(x,y)= | 1 2-2x |
,f(-x,-y)=- | 1 2x |
どうやら、上の処方に従うと、やはりf(x,y)=1の方に軍配が上がるようです。
ただし、これはあくまでユークリッド空間で考えればの話で、実験結果が1/4になるのもそれがポイントです。
別の幾何学を持ってくれば、別の確率分布がでるかもしれません。
やはり、答えは一つではないようです。
◆愛知県 Y.M.Ojisan さんからのコメント。
【A-Leoさんのコメントへのコメント】
最初に、これは反論ではなく他の解釈を示すものであることを申し述べておきます。
f(x,y)はx,yともに実際は0~1でのみ定義しており
f(-x,-y)の値はありません。
従って逆に f(-x,-y)=f(x,y)とここで改めて定義し、すぐには降参しないようにできます。
最終的には、x,yを一次元空間に同時にほうり投げたときの確率密度は
f(x,y)=1が最も穏当という点で異論はありま
せん。
私の示した確率分布は次のように考えられます。
最初にxを一次元空間にほうりなげ,
そこで最も穏当な確率密度 f(x)=1を用います。
次に切ったものに対して右か左かの2値空間で
f(右)=f(左)=1/2という最も穏当な確率を設定し、
最後にその選択された側の切り方:yに対して
一次元空間で最も穏当な確率f(y)=1を用いています。
パラドクスのようでもありますが、何せ人間が切るのですから矛盾はつきものかも。^/^
勿論ここでの元凶は左右2値を同確率とした点にあるわけですが、
この場合その元になる「x切り」の構造が既知なので
その同一でない確率x:1-xを特定できます。
でも知らなければ同値が穏当となってしまうわけです。 逆にxに関してもその構造を知らないので一様が穏当としていますが、大きなはさみを使い、肩を中心に角度という一次元に関して一様と すれば、xは一様でない確率密度に従います。
◆出題者のコメント。
ippei さん、Y.M.Ojisan さん、解答ありがとうございます。
それから、A-Leo さん、貴重なコメントありがとうございます。
| 【問題1】は、 | 1 4 |
で正解です。 |
| ところで、Y.M.Ojisan さんの【PS2】の場合ですが、私なりに求めてみると確率 | 1 6 |
になりました。 |
【問題2】のY.M.Ojisan さんの解答は条件を満たしている作図なので、正解とします。
ただし、直角三角形の特性を利用すると、もっと簡単な作図法があります。
面積の2等分線を含めても、コンパス2回,定規2回だけで可能です。
よろしければ挑戦してみてください。
それから、任意の三角形に適用できる作図法は実に巧みですね。
任意の三角形でも出題したかったのですが、私にはこの作図法が発見できませんでした。(^^;
◆出題者のFootmark さんからの解答。
【問題1】
切断によってできた3本の線分で三角形ができるためには、
3本の線分のそれぞれの長さが三角不等式を満たさなければならない。
つまり、任意の2本の長さの和が残った1本より長くなければならない。
明らかに、どの1本であっても元の線分の半分以上の長さなら、三角不等式を満たさない。
逆に、3本とも元の線分の半分未満の長さなら、常に三角不等式を満たす。
よって、求める確率は「3本の線分のどの長さも元の線分の半分未満となる確率」と同値である。
そこで、仮に1つ目の切断がされたものとすると、線分は図のような2本になる。
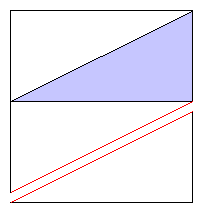
図では、便宜的に長い方の線分を上に短い方の線分を下にしたが、
横方向は1つ目の切断によるすべてのケースを表している。
明らかに、三角形ができる2つ目の切断位置は図の青い部分でなければならない。
(長い方の線分で、両端のどちらからも元の線分の半分未満の距離にある部分)
よって、
| 三角形ができる確率 |
| = | 青い部分の面積 全体の面積 |
| = | 1 4 |
。 |
◆ Y.M.Ojisan さんの【PS2】の場合 ◆
| 三角形ができる確率 |
| = | 2つ目の切断が長い方の線分となる確率 × | 青い部分の面積 長い方の線分での全体の面積 |
| = | 1 2 |
× | 1 3 |
| = | 1 6 |
。 |
◆愛知県 Y.M.Ojisan さんからのコメントと解答。
【1本の線分と三角形出題者へのコメント】
【問題1コメント】
コメントありがとうございます。
ミスが発見できました。
赤字部修正いたします。
| 0.5 ∫ 0 |
x 2-2x |
dx+ | 1 ∫ 0.5 |
1-x 2x |
dx |
| = | 1 ∫ 0.5 |
1-x x |
dx |
| =ln(2)- | 1 2 | =0.193<0.25 |
しかし私の意図する意味においてはやはり1/6ではありません。
違いがどこにあるかというと、x=0において長いほうのどこかを切る確率を1としたとき、出題者の図ではx=0.5において長いほうのどこかを切る確率が0.5に成ってしまいます。
途中で短いほうを切らないとした従属条件が単純な面積比では反映されていません。
【問題2解答】
単純な想定は未熟な発想でした。
なるほど、次の方法でしょうか。
AB>ACとします。
これは簡単です。
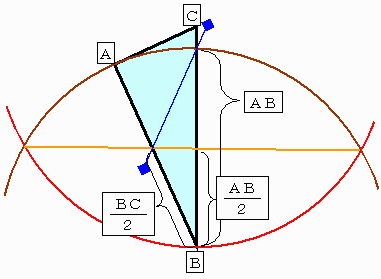
◆出題者のコメント。
Y.M.Ojisan さん、【問題2】正解です。
このとき、2等分した一方(最小頂角がある方)が二等辺三角形となるのが面白いですね。
以下、Y.M.Ojisan さんの【問題1】【PS2】の解答に対するコメントです。
>出題者の図ではx=0.5において長いほうのどこかを切る確率が0.5に成ってしまいます。
これって、最初中点で切断したときのことですよね。
切断位置が元の線分の中点にあると、明らかに三角不等式を満たしません。
それ故、三角形ができるためには、中点は切断位置から除外しなければなりません。
| ところが、切断位置が中点である確率は | 1 ∞ |
で、ほとんど0です。 |
私の図の右端を見ていただければ判るように、
このとき長い方を切断して三角不等式を満たす確率は1です。
1つ目の切断が済むと、2つ目の切断は長い方か短い方のいずれかでしなければなりません。
ところが、短い方を切断したのでは、明らかに三角不等式を満たしません。
よって、
三角形ができる確率
= 長い方が切断される確率 × 長い方の切断で三角不等式を満たす確率
【PS1の場合】
| 三角形ができる確率 |
| = | 長い方の面積(3) 全体の面積(4) |
× | 青い部分の面積(1) 長い方の面積(3) |
| = | 青い部分の面積(1) 全体の面積(4) |
| = | 1 4 |
| 三角形ができる確率 |
| = | 1 2 |
× | 青い部分の面積(1) 長いの方の面積(3) |
| = | 1 6 |
◆愛知県 Y.M.Ojisan さんからのコメント。
【PS2に関するコメント2】
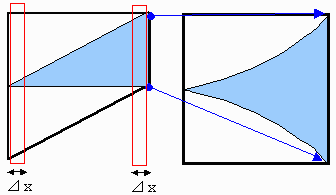
たとえば下左図の赤枠の同じ⊿xの部分の確率を比べてください。
左赤枠側は殆ど成立せず、右赤枠側は殆ど成立し⊿xが同じなので成立する確率はこの範囲で1/2であるべきです。
しかし出題者の数え方によれば1/3に成ってしまいます。
面積比で確率を出そうとするなら、右図のように全部同じ高さに不等に引き伸ばす必要があります。
よって1/3より多く、1/2より小さくなります。
◆出題者のコメント。
Y.M.Ojisan さん、失礼しました。(^^;
前回のコメントで、やっと理解できました。
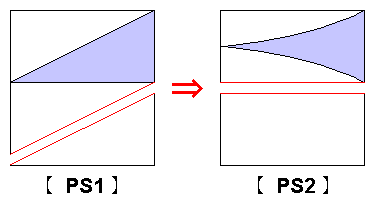
【PS1】なら、2つ目の切断がされる2本それぞれの確率は、各線分の長さに比例する。
それ故、長い方にある線分でも図の左端の線分は右端の線分の2倍の確率で2つ目の切断がされる。
ところが、
【PS2】なら、どんなケースの2本であっても2つ目の切断がされる2本の確率が等しいため、
長い方にある異なる長さのどんな線分も、2つ目の切断がされる確率はすべて等しい。
結局、こういうことだったんですね。
頭の固い出題者に何回もご説明いただき、ありがとうございました。