『同異等率混合状態』解答

◆静岡県　ヨッシー さんからの解答。

【問題１】

答え：ある

証明：

それぞれの球数を ｍ,ｎ （ｍ≧ｎ≧１）とすると、
全ての玉の取り出し方は、m+nＣ2 通り

同色を２個取り出す取り出し方は、
mＣ2＋nＣ2 通り

問題の条件を満たすには、
m+nＣ2 ＝ ２(mＣ2＋nＣ2) となればよい。

計算すると、
(m+n)(m+n-1)
2		＝ m(m-1) + n(n-1)

整理して
　m2-(2n+1)m+n2-n = 0

m について解くと、

　

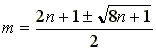
３以上の奇数 2k+1(kは自然数) について、
　(2k+1)2=8n+1 とおくと

n= k(k+1)
2		 ・・・常に自然数

このとき m は、
m= (k+1)(k+2)
2		 または k(k-1)
2

m, n の大小を考慮して整理すると、３つの連続する自然数
k, k+1, k+2 (k は自然数) について、

m= (k+1)(k+2)
2		,n= k(k+1)
2

で表される自然数 m, n が問題の条件を満たす２数である。

◆東京都　BossF さんからの解答。

【問題１】

同種は、 mC2+nC2
m+nC2

異種は、 mC1・nC1
m+nC2

よって題意は,

mC2+nC2= mC1・nC1

すなわち、 m(m-1)
2		+ n(n-1)
2		=mn…(1) と同値

ところで、(1)より

(m-n)2=m+n

よって　m-n=k(≧0)…(2)　とおけば、
m+n=k2…(3)

(2),(3)より

m= k(k+1)
2		,n= k(k-1)
2		　(但し,n≧1より,k≧2)…(4)

逆に(4)のとき(1)はみたされる

よって求める一般解は

m= k(k+1)
2		,n= k(k-1)
2		　(k≧2)

◆広島県　清川　育男 さんからの解答。

【問題１】

mC2+nC2=m*n・・・(1)

Ak= k(k+1)
2		　k:自然数

m=Ak+1
n=Ak
(1)の左辺=k*(k+1)2*(k+2)
4

(1)の右辺=k*(k+1)2*(k+2)
4

m,nは(1)式を満たす。

◆出題者のコメント。

早々に解答ありがとうございます。
一般項のはじまりが第１項と第２項の違いのため式は異なりますが、皆さんみごと正解です。

不定方程式の問題としては比較的易しかったかも・・。
そこで、さらに一般化させた【問題２】,【問題３】を追加します。

今後は統一したいので、一般項は第１項からはじまるようにしてください。

◆広島県　清川　育男 さんからの解答。

【問題２】

参考までに、、、。

pC2+qC2+rC2=p*q+q*r+r*p

プログラムを組んで必要条件を調べてみました。
解の系を一般式であらわすのは(再帰的方法でないと)困難と思われます。
特にrは。

rの必要条件は、
r≡0 or r≡1 (mod 3) と予測されます。
またｒはそれまでに解の確定したｑの解の系に含まれていなければならないようです。　

ｐはｑの（ｎ+１）
2次の係数は（ｒ*２+１）

ｒ＝１〜１００までチェックしました。

r=1 1個の系
r=45,66 4個の系
その他 　2個の系　

　REM 3元２次不定方程式の解析プログラム
　REM DATA文は予備プログラムから 

　DATA 1,3,9,18,30
　DATA 3,6,19,39,66
　DATA 3,9,24,46,75
　DATA 6,10,33,69,118
　DATA 6,19,48,90,145
　DATA 9,18,54,109,183
　DATA 9,24,64,123,201
　DATA 10,15,51,108,186
　DATA 10,33,81,150,240
　DATA 15,21,73,156,270
　DATA 15,51,123,226,360
　DATA 18,30,96,199,339
　DATA 18,54,136,255,411
　DATA 19,39,114,228,381
　DATA 19,48,129,249,408
　DATA 21,28,99,213,370
　DATA 21,73,174,318,505
　DATA 24,46,138,279,469
　DATA 24,64,168,321,523
　DATA 28,36,129,279,486
　DATA 28,99,234,426,675
　DATA 30,45,150,316,543
　DATA 30,96,235,435,696
　DATA 33,69,199,396,660
　DATA 33,81,219,424,696
　DATA 36,45,163,354,618
　DATA 36,129,303,550,870
　DATA 39,66,208,429,729 
　DATA 39,114,288,541,873
　DATA 45,55,201,438,766
　DATA 45,63,216,460,795
　DATA 45,150,361,663,1056
　DATA 45,163,381,690,1090
　DATA 46,75,240,498,849
　DATA 46,138,345,645,1038
　DATA 48,90,271,549,924
　DATA 48,129,336,640,1041
　DATA 51,108,309,613,1020
　DATA 51,123,334,648,1065
　DATA 54,109,318,636,1063
　DATA 54,136,363,699,1144
　DATA 55,66,243,531,930
　DATA 55,201,468,846,1335
　DATA 63,84,294,631,1095
　DATA 63,216,514,939,1491
　DATA 64,123,366,738,1239
　DATA 64,168,441,843,1374
　DATA 66,78,289,633,1110
　DATA 66,100,330,693,1189
　DATA 66,208,510,945,1513
　DATA 66,243,564,1018,1605
　DATA 69,118,369,759,1288
　DATA 69,199,504,948,1531
　DATA 73,156,444,879,1461
　DATA 73,174,474,921,1515
　DATA 75,111,370,780,1341
　DATA 75,240,585,1081,1728
　DATA 78,91,339,744,1306
　DATA 78,289,669,1206,1900
　DATA 81,150,453,919,1548
　DATA 81,219,568,1080,1755
　DATA 84,108,384,829,1443
　DATA 84,294,694,1263,2001
　DATA 90,145,465,966,1648
　DATA 90,271,675,1260,2026
　DATA 91,105,393,864,1518
　DATA 91,339,783,1410,2220
　DATA 96,199,573,1140,1900
　DATA 96,235,633,1224,2008
　DATA 99,213,604,1194,1983
　DATA 99,234,639,1243,2046
　DATA 100,141,480,1020,1761
　DATA 100,330,795,1461,2328

　LET  Z=0
　FOR I=1 TO 73 
 　  READ A,B1,B2,B3,B4   
   　REM Q=I2*N^2+I1*N+I0の探索
   　FOR I2=3 TO 201
    　  FOR I1=1 TO 339
      　   FOR I0=0 TO 156         
        　    IF B1=(I2+I1+I0)/2 AND B2=(I2*4+I1*2+I0)/2 THEN
          　     IF B3=(I2*9+I1*3+I0)/2 AND B4=(I2*16+I1*4+I0)/2 THEN
            　      LET  Z=Z+1
              　    LET  R1=REMAINDER(A,3)
                　  PRINT USING "###":Z;
                  　PRINT ") ";
                  　LET  X$="("&STR$(I2)&"*N^2+"&STR$(I1)&"*N+"&STR$(I0)&")/2"
                  　PRINT "R=";
                  　PRINT USING "###":A;
                  　PRINT "(";
                  　PRINT R1;
                  　PRINT ")";            
                  　PRINT "  ";
                  　PRINT "Q=";
                  　PRINT X$;
                  　REM P=I2*N^2+(I2*2+I1)*N+I2+I1+10
                  　PRINT "  ";
                  　LET  Y$="("&STR$(I2)&"*N^2+"&STR$(I2*2+I1)&"*N+"&STR$(I2+I1+I0)&")/2"
                  　PRINT "P=";
                  　PRINT Y$
               　END IF
            　END IF
         　NEXT I0
      　NEXT I1
   　NEXT I2
　NEXT I
　END

　1) R=  1( 1 )  Q=(3*N2+3*N+0)/2        P=(3*N2+9*N+6)/2
  2) R=  3( 0 )  Q=(7*N2+5*N+0)/2        P=(7*N2+19*N+12)/2
  3) R=  3( 0 )  Q=(7*N2+9*N+2)/2        P=(7*N2+23*N+18)/2
  4) R=  6( 0 )  Q=(13*N2+7*N+0)/2       P=(13*N2+33*N+20)/2
  5) R=  6( 0 )  Q=(13*N2+19*N+6)/2      P=(13*N2+45*N+38)/2
  6) R=  9( 0 )  Q=(19*N2+15*N+2)/2      P=(19*N2+53*N+36)/2
  7) R=  9( 0 )  Q=(19*N2+23*N+6)/2      P=(19*N2+61*N+48)/2
  8) R= 10( 1 )  Q=(21*N2+9*N+0)/2       P=(21*N2+51*N+30)/2
  9) R= 10( 1 )  Q=(21*N2+33*N+12)/2     P=(21*N2+75*N+66)/2
 10) R= 15( 0 )  Q=(31*N2+11*N+0)/2      P=(31*N2+73*N+42)/2
 11) R= 15( 0 )  Q=(31*N2+51*N+20)/2     P=(31*N2+113*N+102)/2
 12) R= 18( 0 )  Q=(37*N2+21*N+2)/2      P=(37*N2+95*N+60)/2
 13) R= 18( 0 )  Q=(37*N2+53*N+18)/2     P=(37*N2+127*N+108)/2
 14) R= 19( 1 )  Q=(39*N2+33*N+6)/2      P=(39*N2+111*N+78)/2
 15) R= 19( 1 )  Q=(39*N2+45*N+12)/2     P=(39*N2+123*N+96)/2
 16) R= 21( 0 )  Q=(43*N2+13*N+0)/2      P=(43*N2+99*N+56)/2
 17) R= 21( 0 )  Q=(43*N2+73*N+30)/2     P=(43*N2+159*N+146)/2
 18) R= 24( 0 )  Q=(49*N2+37*N+6)/2      P=(49*N2+135*N+92)/2
 19) R= 24( 0 )  Q=(49*N2+61*N+18)/2     P=(49*N2+159*N+128)/2
 20) R= 28( 1 )  Q=(57*N2+15*N+0)/2      P=(57*N2+129*N+72)/2
 21) R= 28( 1 )  Q=(57*N2+99*N+42)/2     P=(57*N2+213*N+198)/2
 22) R= 30( 0 )  Q=(61*N2+27*N+2)/2      P=(61*N2+149*N+90)/2
 23) R= 30( 0 )  Q=(61*N2+95*N+36)/2     P=(61*N2+217*N+192)/2
 24) R= 33( 0 )  Q=(67*N2+59*N+12)/2     P=(67*N2+193*N+138)/2
 25) R= 33( 0 )  Q=(67*N2+75*N+20)/2     P=(67*N2+209*N+162)/2
 26) R= 36( 0 )  Q=(73*N2+17*N+0)/2      P=(73*N2+163*N+90)/2
 27) R= 36( 0 )  Q=(73*N2+129*N+56)/2    P=(73*N2+275*N+258)/2
 28) R= 39( 0 )  Q=(79*N2+47*N+6)/2      P=(79*N2+205*N+132)/2
 29) R= 39( 0 )  Q=(79*N2+111*N+38)/2    P=(79*N2+269*N+228)/2
 30) R= 45( 0 )  Q=(91*N2+19*N+0)/2      P=(91*N2+201*N+110)/2
 31) R= 45( 0 )  Q=(91*N2+33*N+2)/2      P=(91*N2+215*N+126)/2
 32) R= 45( 0 )  Q=(91*N2+149*N+60)/2    P=(91*N2+331*N+300)/2
 33) R= 45( 0 )  Q=(91*N2+163*N+72)/2    P=(91*N2+345*N+326)/2
 34) R= 46( 1 )  Q=(93*N2+51*N+6)/2      P=(93*N2+237*N+150)/2
 35) R= 46( 1 )  Q=(93*N2+135*N+48)/2    P=(93*N2+321*N+276)/2
 36) R= 48( 0 )  Q=(97*N2+71*N+12)/2     P=(97*N2+265*N+180)/2
 37) R= 48( 0 )  Q=(97*N2+123*N+38)/2    P=(97*N2+317*N+258)/2
 38) R= 51( 0 )  Q=(103*N2+93*N+20)/2    P=(103*N2+299*N+216)/2
 39) R= 51( 0 )  Q=(103*N2+113*N+30)/2   P=(103*N2+319*N+246)/2
 40) R= 54( 0 )  Q=(109*N2+91*N+18)/2    P=(109*N2+309*N+218)/2
 41) R= 54( 0 )  Q=(109*N2+127*N+36)/2   P=(109*N2+345*N+272)/2
 42) R= 55( 1 )  Q=(111*N2+21*N+0)/2     P=(111*N2+243*N+132)/2
 43) R= 55( 1 )  Q=(111*N2+201*N+90)/2   P=(111*N2+423*N+402)/2
 44) R= 63( 0 )  Q=(127*N2+39*N+2)/2     P=(127*N2+293*N+168)/2
 45) R= 63( 0 )  Q=(127*N2+215*N+90)/2   P=(127*N2+469*N+432)/2
 46) R= 64( 1 )  Q=(129*N2+99*N+18)/2    P=(129*N2+357*N+246)/2
 47) R= 64( 1 )  Q=(129*N2+159*N+48)/2   P=(129*N2+417*N+336)/2
 48) R= 66( 0 )  Q=(133*N2+23*N+0)/2     P=(133*N2+289*N+156)/2
 49) R= 66( 0 )  Q=(133*N2+61*N+6)/2     P=(133*N2+327*N+200)/2
 50) R= 66( 0 )  Q=(133*N2+205*N+78)/2   P=(133*N2+471*N+416)/2
 51) R= 66( 0 )  Q=(133*N2+243*N+110)/2  P=(133*N2+509*N+486)/2
 52) R= 69( 0 )  Q=(139*N2+85*N+12)/2    P=(139*N2+363*N+236)/2
 53) R= 69( 0 )  Q=(139*N2+193*N+66)/2   P=(139*N2+471*N+398)/2
 54) R= 73( 1 )  Q=(147*N2+135*N+30)/2   P=(147*N2+429*N+312)/2
 55) R= 73( 1 )  Q=(147*N2+159*N+42)/2   P=(147*N2+453*N+348)/2
 56) R= 75( 0 )  Q=(151*N2+65*N+6)/2     P=(151*N2+367*N+222)/2
 57) R= 75( 0 )  Q=(151*N2+237*N+92)/2   P=(151*N2+539*N+480)/2
 58) R= 78( 0 )  Q=(157*N2+25*N+0)/2     P=(157*N2+339*N+182)/2
 59) R= 78( 0 )  Q=(157*N2+289*N+132)/2  P=(157*N2+603*N+578)/2
 60) R= 81( 0 )  Q=(163*N2+117*N+20)/2   P=(163*N2+443*N+300)/2
 61) R= 81( 0 )  Q=(163*N2+209*N+66)/2   P=(163*N2+535*N+438)/2
 62) R= 84( 0 )  Q=(169*N2+45*N+2)/2     P=(169*N2+383*N+216)/2
 63) R= 84( 0 )  Q=(169*N2+293*N+126)/2  P=(169*N2+631*N+588)/2
 64) R= 90( 0 )  Q=(181*N2+97*N+12)/2    P=(181*N2+459*N+290)/2
 65) R= 90( 0 )  Q=(181*N2+265*N+96)/2   P=(181*N2+627*N+542)/2
 66) R= 91( 1 )  Q=(183*N2+27*N+0)/2     P=(183*N2+393*N+210)/2
 67) R= 91( 1 )  Q=(183*N2+339*N+156)/2  P=(183*N2+705*N+678)/2
 68) R= 96( 0 )  Q=(193*N2+169*N+36)/2   P=(193*N2+555*N+398)/2
 69) R= 96( 0 )  Q=(193*N2+217*N+60)/2   P=(193*N2+603*N+470)/2
 70) R= 99( 0 )  Q=(199*N2+185*N+42)/2   P=(199*N2+583*N+426)/2
 71) R= 99( 0 )  Q=(199*N2+213*N+56)/2   P=(199*N2+611*N+468)/2
 72) R=100( 1 )  Q=(201*N2+75*N+6)/2 　  P=(201*N2+477*N+282)/2
 73) R=100( 1 )  Q=(201*N2+327*N+132)/2  P=(201*N2+729*N+660)/2

◆愛知県　Y.M.Ojisan さんからの解答。

【問題２】

Ｋ：６以上の整数
Ｍ：＝４Ｋ2＋３
Ｈ：Ｍの約数で 以上　Ｍ未満のもの
ｈ：＝ Ｍ
Ｈ

このとき
　ｒ＝ ｈ−１
２
　ｑ＝ Ｈ−４Ｋ＋ｈ−４
８
　ｐ＝　ｑ＋Ｋ

は　同異等率　で　ｐ≧ｑ≧ｒ≧１　である。

∵【十分性】

  1. 同異等率になることは代入して計算すれば良いので省略。

  2. Ｍはその定義から奇数であり、約数のＨ，ｈは奇数である。
    よってｒは整数である。

  3. HはＭ未満で正だからｈは１より大きい。
    よってｒ≧１である。

  4. q−r≧を解くと　
    Ｈ≧ が得られるので
    q≧ｒである。詳細略

  5. ｐ＝ｑ＋Ｋであり、Ｋは６以上整数だから
    ｐはｑが整数なら整数でp≧qである。

  6. ｑが整数になることは、Ｋを奇数と偶数に分ければ証明できる。

【証明】

(1) Ｋ＝2y+1のとき　（ｙ：整数）

Ｍ＝16y2+16y+７

　

ｑ＝

16y2+16y+７
ｈ		−8y−4＋ｈ−4
8
　＝y−１＋ (16y2+16y+7)＋(4ｒ2+4ｒ+1)
8ｈ
　

　＝y−１＋

(ｒ+1)ｒ
2		 ＋2y2+2y+1
ｈ
　＝整数　＋ 整数
奇数

であり、分母に因数２は残らない。

以上よりqの分子：Ｈ−４Ｋ＋ｈ−４　は　８の倍数である。
よって、ｑは整数である。

(2) Ｋ＝2yのとき　（ｙ：整数）

Ｍ＝16y2+3

　

ｑ＝

16y2+3
ｈ		−8y＋ｈ−8+4
8
　＝y−１＋ (16y2+8y+7)＋(4ｒ2+4ｒ+1)
8ｈ
　

　＝y−１＋

(ｒ+1)ｒ
2		 ＋2y2+y+１
ｈ
　＝整数　＋ 整数
奇数

であり、分母に因数２は残らない。

以上よりqの分子：Ｈ−４Ｋ＋ｈ−４　は　８の倍数である。

よって、ｑは整数である。

以上(1)(2)より　ｑは整数である。

【必要性】

ＨがＭの約数である必要性のみ証明する。その他省略。

ｒが整数であるので　ｈ＝２ｒ＋１は整数でなければならない。
よって　８ｑ＝Ｈ−４Ｋ＋ｈ−４　であって、Ｈ以外は整数である。
故に、Ｈは整数である。
即ち　Ｍ＝Ｈ＊ｈであるから　Ｈ、ｈはＭの約数でなければならない。

【問題１の包含】

問題２の系列で　Ｋの範囲を２以上とし、Ｈ＝Ｍとすると問題１の正解の系列が得られる。
Ｋ＝k+1に置き換えると，ｈ＝１だから　ｒ＝０

ｑ＝ ４Ｋ2＋３−４Ｋ＋１−４
８
　＝ Ｋ（Ｋ−１）
２
　＝ (k+1)k
２

ｒ＝ｑ＋Ｋ＝ Ｋ（Ｋ＋１）
２		＝ (k+2)(k+1)
２

すなわち、問題２の系列はＫとＨの範囲を広げることで、問題１をその特殊な場合として含む。

【Ｐ．Ｓ．】

残念ながら、この先に一般解【問題３】はなさそうです。
【問題１】のようにパラメータ（この場合２個）に対して常に１対１に存在するような系列というのではないところがイマイチです。
前向きに言えば，Ｍの因数分解をクリアすれば機械的に作ることが可能といえます。

清川さんのように先にｒ（ｈ＝２ｒ＋１）を与えてもよく、
４Ｋ2＋３　がｈの倍数であるＫを使う方法もあります。

その意味で素因数分解という良く知られた難問に、ややこしいところを押し込めただけで、清川流と大差はないわけです。

なお、ｒ mod 3≠２？ 予測は　
４Ｋ2＋３の素因数 mod 3≠２　なる一見単純な問題に置き換えられます。

◆出題者のコメント。

解答ありがとうございます。

ご指摘のように【問題２】【問題３】を一般式で表すには無理がありました。
大変申し訳なく思っています。

それにしても、「清川　育男 」さんの予測と「Y.M.Ojisan」 さんの一般解には頭が下がります。

一般式が可能な【新問題２】【新問題３】を追加します。

　『同異等率混合状態』へ

　数学の部屋へもどる