)にｒだけ移動して座標(ｍ，ｎ)に着いたとすると、右(
)には(ｍ−ｒ)だけ、上(
)には(ｎ−ｒ)だけ移動していることになる。◆広島県 清川 育男 さんからの解答。
【問題１】
青の移動は（黒赤）、（赤黒）の移動に等しい。
２５２＋６３０＋５６０＋２１０＋３０＋１＝１６８３
答え １６８３通り。
３，１３，６３，３２１，１６８３，８９８９，４８６３９，
数列サイトによるとDelannoy mumbersと言うそうです。
問題２は自由度の関係で考えがもやっています。
【問題２】
青４、黒４、赤６の移動性がある。
２１０＋５０４＋４２０＋１４０＋１５＝１２８９
答え １２８９通り。
【コメント】
全く不勉強でこの数列の名前は初耳です。
水の流れさん、どうでしょう。
◆岐阜県 水の流れ さんからのコメント。
＜解説＞
座標(ｍ，ｎ)までたどり着く経路の総数をＳ(ｍ，ｎ)とすると、
Ｓ(０，０)＝１，Ｓ(−１，ｎ)＝Ｓ(ｎ，−１)＝０で
漸化式
Ｓ(ｍ，ｎ)＝Ｓ(ｍ，ｎ−１)＋Ｓ(ｍ−１，ｎ−１)＋Ｓ(ｍ−１，ｎ)
が成り立ちます。それに従って計算して、図の中に示します。
| ６ | １ | 13 | 85 | 377 | 1289 | 3653 | 8989 |
| ５ | １ | 11 | 61 | 231 | 681 | 1683 | 3653 |
| ４ | １ | ９ | 41 | 129 | 321 | 681 | 1289 |
| ３ | １ | ７ | 25 | 63 | 129 | 231 | 377 |
| ２ | １ | ５ | 13 | 25 | 41 | 61 | 85 |
| １ | １ | ３ | ５ | ７ | ９ | 11 | 13 |
| ０ | １ | １ | １ | １ | １ | １ | １ |
| S(m,n) | ０ | １ | ２ | ３ | ４ | ５ | ６ |
問１ Ｓ(５，５)＝１６８３
問２ Ｓ(６，４)＝１２８９
問３ 座標(０，０)から(ｍ，ｎ)について、具体的に求めてみます。
駒が斜め上()にｒだけ移動して座標(ｍ，ｎ)に着いたとすると、
右()には(ｍ−ｒ)だけ、上()には(ｎ−ｒ)だけ移動していることになる。
したがって、
斜め上()をｒ個、
右()を(ｍ−ｒ)個、
上()を(ｎ−ｒ)個を並べる組み合わせの数から、
(ｍ＋ｎ−ｒ)！÷ｒ！(ｍ−ｒ)！(ｎ−ｒ)！ になります。
次に、を選ぶ方法は ０≦ｒ≦ Min(ｍ，ｎ) ですから、
総数Ｓ(ｍ，ｎ)は
| Min(m,n) Σ r=0 | (ｍ＋ｎ−ｒ)！÷ｒ！(ｍ−ｒ)！(ｎ−ｒ)！ |
(ただし、Min(ｍ，ｎ)はｍ、ｎのうちで大きくない方を表すものとする)
問１で調べてみます。
ｒ＝０のとき、１０！／５！５！＝２５２
ｒ＝１のとき、９！／４！４！＝６３０
ｒ＝２のとき、８！／２！３！３！＝５６０
ｒ＝３のとき、７！／３！２！２！＝２１０
ｒ＝４のとき、６！／４！＝３０
ｒ＝５のとき、５！／５！＝１
よって、２５２＋６３０＋５６０＋２１０＋３０＋１＝１６８３ (答)
問２で調べてみます。
ｒ＝０のとき、１０！／６！４！＝２１０
ｒ＝１のとき、９！／５！３！＝５０４
ｒ＝２のとき、８！／２！４！２！＝４２０
ｒ＝３のとき、７！／３！３！＝１４０
ｒ＝４のとき、６！／４！２！＝１５
よって、２１０＋５０４＋４２０＋１４０＋１５＝１２８９ (答)
＜研究＞
座標(ｍ，ｎ)までたどり着く経路の総数Ｓ(ｍ，ｎ)の値を三角形状に並べてみます。
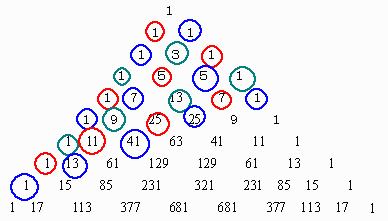
図のように斜めに足していくと、トリボナッチ数列 Ｔ(ｎ)を得ることができます。 Ｔ(１)＝１
Ｔ(２)＝１＋１＝２
Ｔ(３)＝１＋３＝４
Ｔ(４)＝１＋５＋１＝７
Ｔ(５)＝１＋７＋５＝１３
Ｔ(６)＝１＋９＋１３＋１＝２４
Ｔ(７)＝１＋１１＋２５＋７＝４４
Ｔ(８)＝１＋１３＋４１＋２５＋１＝８１
・・・・・・・・
また、この数列は次のような大相撲の星取り表の中にもでてきます。
大相撲の本場所で、３連敗しない方法(２連敗まで許される)勝ち負けの起こり方は
１，２，３，４，・・・、１５日目ではどんな数列になるでしょう。
皆さん、考えてください。
◆広島県 清川 育男 さんからの解答。
【問題１】
数列サイトによると、別の角度からの漸化式が載っていました。
ａ1＝１、ａ2＝１としたとき
| ａn＝ | ３(２ｎー５)ａn-1−(ｎ−３)ａn-2 ―――――――――――――――― ｎ−２ |
１，１，３，１３，６３，３２１，．．．，
一つずれますが。
以上報告します。
水野先生の研究による影に隠されたトリボナッチ数列の発見はすばらしいですね。
奥の深さに驚かされます。