『フィボナッチ数列の性質 Part3』解答

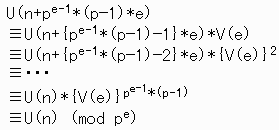
◆広島県　清川　育男 さんからの解答。

証明は出来ないのですが、推理しました。

F(2n-2) n≧2　でしょうか。

フィボナッチのことはフィボナッチに聞けと言った感じです。
それにしても不思議な数列です。

◆埼玉県　\aleph_0 さんからの解答。

F_nに限らず、一般の整数mを法とするFibonacci数の周期について考えたいと思います。
ただし、全容が完全に明らかになっているわけではありませんので、現在分かっていることを以下で述べていきます。

まず次のように定義します。

定義1. 整数mに対してΠ(m)を法mに関する(F_n)の周期の集合とする。
Π(m)＝{r∈Z|F_n＋r≡F_n (mod m) (∀n∈Z)}.

ここで次の補題を準備します。
（証明は『多項式の列』を参照。）

補題1. 任意の整数m,nに対して、
F_m＋n＝F_m＋1F_n＋F_mF_n−1.

これを用いると、Π(m)は次のように特徴付けられます。

命題2. 整数rに対して、
r∈Π(m) ⇔ F_r＋1≡F_r−1≡1 (mod m).

一方、Π(m)は明らかにZのイデアルですから、
ある整数π(m)＞0により生成されます：Π(m)＝(π(m)).
（すなわち、π(m)は法mに関する基本周期。）
また、定義より次の命題が容易に示されます。

命題3. 整数m,m'に対して、
(a) m|m'ならば、Π(m)⊃Π(m')、
　すなわち、π(m)|π(m').

(b) (m,m')＝1ならば、Π(mm')＝Π(m)∩Π(m')、
　すなわち、π(mm')はπ(m)とπ(m')の最小公倍数。

命題3(b)より、mが素巾の場合に帰着することが分かります。
そこで、次の補題を準備します。

補題4. m,nを整数とするとき、任意の整数k≧0に対して、

Fmn±1＝

k �� i＝0

kCi Fn±1k−iFniF(m-k)n±(1-i). （複号同順）

特にk＝mとおけば、m≧0に対して、

Fmn±1＝

m �� i＝0

mCi Fn±1m−iFniF±(1-i). （複号同順）

これは補題1を用いて、kに関する帰納法により示されます。
これを用いると、次の命題が示されます。

命題5. pを素数、e≧1を整数とし、
簡単のためr＝π(p^e)とおく。

(a) p≠2またはe≠1のとき、
　F_pr±1≡F_r±1^p (mod p^e＋2). （複号同順）

(b) p≠2またはe≠1のとき、
　F_r±1≡1＋ap^e (mod p^e＋1) (a∈Z) ⇒ F_pr±1≡1＋ap^e＋1 (mod p^e＋2). （複号同順）
(c) π(p^e＋1)＝π(p^e)またはpπ(p^e).

(d) π(pe)≠π(pe＋1) ⇒ π(pe＋1)≠π(pe＋2).

Fr±1≡1＋ape＋bpe＋1(mod pe＋2)

Fpr±1≡Fr±1p≡(1＋ape＋bpe＋1)p≡1＋ape＋1(mod pe＋2).

これより次の系が直ちに従います。

系6. 素数pに対してu≧1をπ(p)＝π(p^u)となる最大の整数とすると、
任意の整数e≧uに対してπ(p^e)＝p^e−uπ(p).
特にπ(p)≠π(p²)ならば、任意の整数e≧1に対してπ(p^e)＝p^e−1π(p).

以上よりm＝pが素数の場合に帰着することが分かります。
そこで、以下では有限体F_p上で考えることにします。
まず(F_n)の特性多項式Φ(X)＝X²−X−1の判別式は
D＝1²−4(−1)＝5であることに注意します。
よって、p≠5ならば、Φ(X)は相異なる根φ,φ'をもち、次が成立します。

(1) φ＋φ'＝1, φφ'＝−1,
(2) F_n＝(φⁿ−φ'ⁿ)(φ−φ')⁻¹ (n∈Z).

このとき、Π(p)は次のように特徴付けられます。

命題7. 整数rに対して、
r∈Π(p) ⇔ φ^r＝φ'^r＝1.
特にπ(p)はφ,φ'の位数の最小公倍数である。

証明. (→) (2)より
0＝F₀＝F_r＝(φ^r−φ'^r)(φ−φ')⁻¹,
1＝F₁＝F_r＋1＝(φ^r＋1−φ'^r＋1)(φ−φ')⁻¹.
これらよりφ'^rを消去すれば、φ^r＝1を得る。また同様にφ'^r＝1を得る。
(←) 任意の整数nに対して、(2)より

Fn＋r＝(φn＋r−φ'n＋r)(φ−φ')−1＝(φn−φ'n)(φ−φ')−1＝Fn.

ここでφ,φ'はF_p上高々2次ですから、
命題7よりπ(p)はp²−1の約数であることがわかりますが、より詳しいことを調べるため、場合を分けて考えてみましょう。

まずpが奇素数のとき、(5/p)＝1、
すなわち、p≡±1 (mod 5)ならば、
Φ(X)はF_p上可約であるから、
φ,φ'∈F_p.
したがって、φ^p−1＝φ'^p−1＝1であるから、
命題7よりp−1∈Π(p)を得る。
一方、r＝π(p)に対して再び命題7および(1)の第二式より
(−1)^r＝(φφ')^r＝1であるから、π(p)は偶数である。
なおこのとき、rをφの位数とすれば、
1＝(−1)^2r＝(φφ')^2r＝φ'^2rとなるから、φ'の位数は2rの約数。
逆も同様であるから、φ,φ'の位数は等しいか、一方が他方の2倍になる。

一方、(5/p)＝−1、
すなわち、p≡±2 (mod 5)ならば、
Φ(X)はF_p上既約であるから、
φ,φ'/∈F_p.
このとき、(1)の各式の両辺をp乗すれば、
φ^p＋φ'^p＝1,
φ^pφ'^p＝−1となり、
φ^p,φ'^pもΦ(X)の根であるから、
φ^p＝φ',φ'^p＝φ.
よって、(1)の第二式より
φ^p＋1＝φ'^p＋1＝−1.
したがって、φ^2(p＋1)＝φ'^2(p＋1)＝1であるから、
命題7より2(p＋1)∈Π(p)を得る。
このとき、2(p＋1)/π(p)が偶数であると仮定すると、
π(p)|(p＋1)、
したがって命題7より
φ^p＋1＝φ'^p＋1＝1となり矛盾するから、
2(p＋1)/π(p)は奇数。
特にπ(p)は4の倍数である。
なおこのとき、φ,φ'のF_p上の最小多項式は共にΦ(X)であるから、φ,φ'の位数は等しい。

次にp＝2ならば、Φ(X)＝X²＋X＋1は明らかにF₂上既約であるから、
φ,φ'/∈F₂.
したがって、φ,φ'の位数は2²−1＝3であるから、
命題7よりΠ(2)＝(3)を得る。
（もっとも、この結果は明らかですが。）

最後にp＝5ならば、Φ(X)＝(X−3)²と分解されるから、
F_n＝n3ⁿ⁻¹ (n∈Z)となる。
このとき、r∈Π(5)ならば、任意の整数nに対して

0＝Fn＋r−Fn＝(n＋r)3n＋r−1−n3n−1＝3n−1[(3r−1)n＋r3r]

さて、たいへん長くなりましたが、以上の結果をまとめると次のようになります。

定理8. 法mに関する基本周期π(m)について次が成立する。
(a) 整数mに関する基本周期は、mの素巾因数の基本周期の最小公倍数である。
(b) 素数pに対してu≧1をπ(p)＝π(p^u)となる最大の整数とすると、
任意の整数e≧uに対してπ(p^e)＝p^e−uπ(p).
(c) 素数pに対して、
p＝2ならば、π(2)＝3,
p＝5ならば、π(5)＝20,
p≡±1 (mod 10)ならば、2|π(p)|p−1,
p≡±3 (mod 10)ならば、4|π(p)|2(p＋1).

ここで、未解決の問題として次のようなことが挙げられます。

問題.
(a) 系6に関連して、任意の素数pに対してπ(p)≠π(p²)が成立するか？
(b) 素数p≠2,5に対してπ(p)の正確な値はどのように与えられるか？

(a)については、成立する自明な理由はありませんが、
p＜2³²の範囲で反例は見つかっていません。[2]
一方、(b)については、命題7よりφ,φ'の位数を求めることと同値ですから、かなり難しい問題であると思われます。

References

1. D. D. Wall, Fibonacci series modulo m, Amer. Math. Monthly 67 (1960), pp. 525-532
2. The Fibonacci Numbers, Modulo a prime (http://www-jcsu.jesus.cam.ac.uk/~jmjk2/Fibonacci/Fibonacci.html)

後記

◆広島県　清川　育男 さんからの解答。

\aleph_0 さんからの解答をヒントに再度推理しました。

前回は、F(2),F(3),F(5)から推理しましたが、
F(5)のとき２０のところを２１と数えて間違えました。
今回は大きく開けた感じがします。
F(22)=17711まで成り立ちます。

プログラムを組んで確認しました。

F(n)の剰余の周期は、 n≧4　のとき
　i) nが偶数のとき　2n
　ii) nが奇数のとき　4n

n	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22
F(n)	3	5	8	13	21	34	55	89	144	233	377	610	987	1597	2584	4181	6765	10946	17711
周期	8	20	12	28	16	36	20	44	24	52	28	60	32	68	36	76	40	84	44

証明は出来ませんが、今回は確度が高いと思います。

◆広島県　清川　育男 さんからの解答。

十進ベーシック（１０００桁モード）で確認しました。

フィボナッチ数列を４８２０番目まで用意して、
法F(n)は４番目から１２０５番目まで確認しました。

周期の終わりを、「．．．．，１，０」と仮定しました。

n≧4
　nが偶数　周期　2n
　nが奇数　周期　4n

周期をC(n)とすると、
C(2n+2)+C(2n)=C(2n+1)
C(2n+2)=C(2n+1)-C(2n)
C(4)=8,C(5)=20　n≧2

  REM 周期の問題
  DIM F(4820)
  LET  F(1)=1
  LET  F(2)=1
  FOR N=3 TO 4820
     LET  F(N)=F(N-1)+F(N-2)      
  NEXT N
  LET  A1=-1
  FOR K=4 TO 1205
     IF MOD( K , 2) =0 THEN
        LET  NO=K*2
     ELSE
        LET  NO=K*4
     END IF
     LET  B=F(K)
     LET  Z=0
     FOR I=1 TO 4820
        LET  Z=Z+1
        LET  A=REMAINDER(F(I),B)
        PRINT A;
        REM ....1,0,周期の終わりのパターン
        IF A1=1 AND A=0 THEN
           PRINT
           EXIT FOR
        ELSE 
           LET  A1=A
        END IF
     NEXT I
     PRINT "法はF(";K;")=";B;"周期は";NO;"です。" 
     REM 判定　
     IF (MOD( K , 2) =0 AND Z=2*K) OR (MOD( K , 2) =1 AND Z=4*K) THEN
        PRINT "仮説は成り立つ。"   
     ELSE
        PRINT "反例がありました。"
        EXIT FOR
     END IF     
  NEXT K
  END

◆東京都　安里歩安彼 さんからの解答。

出題者からの解答ですが、じつは自信がなくなってきたので、みなさんに正誤のほどを判断していただきたいと思います。
もし間違っていた場合は、ご指摘お願いします。

補題１．１

　Ｆ_n×Ｆ_n−Ｆ_n-1×Ｆ_n+1
＝−１（ｎが偶数の時）
＝１（ｎが奇数のとき）

証明は、簡単な帰納法で示せるので省略する。

さて、
　（Ｆ_n-1×Ｆ_n-1）−（Ｆ_n-2×Ｆ_n）
＝−１（ｎが奇数の時）
＝１（ｎが偶数の時、）

が成立するので、

　Ｆ_n-1×Ｆ_n-1
≡−１（ｎが奇数の時）、
≡１（ｎが偶数の時）（modＦ_n）

よって、
パターン１：ｎが偶数の時、
　Ｆ_2n-1
≡Ｆ_n-1×Ｆ_n-1
≡１（mod Ｆ_n）となって、
周期は２ｎ。

パターン２：ｎが奇数の時、
　Ｆ_4n-1
≡Ｆ_n-1×Ｆ_n-1×Ｆ_n-1×Ｆ_n-1
≡−１×−１
≡１（mod Ｆ_n）
となって、周期は４ｎ。
また、２ｎとならないことは明らか。

…ということなのですが、どうも自信がないので、お願いします。

◆広島県　清川　育男 さんからの解答。

フィボナッチ数列において法を素数としたとき、剰余の周期と法の関係を予測してみました。

結果は以下の通りです。
５つのパターンに分類出来るのではないかと思います。

１）法 = 2 周期 = 3 周期=法*n+1 型
２）法 = 3 周期 = 8 周期=法*n+2 型
３）法 = 5 周期 = 20 周期=法*n 型．．５のときだけ！！
４）法 = 11 周期 = 10 法=周期*n+1 型
５）法 = 107 周期 = 72 法=(周期/(2^k))*n-1 型

十進ベーシック（１０００桁モード）のプログラムで確認しました。
またフィボナッチ数列において素数２，５は特異な存在のように思われます。

プログラムおよび結果はこちらです。

◆埼玉県　\aleph_0 さんからの解答。

どうやら私は範囲を勝手に拡張して、問題を複雑にしてしまったようです。すみません。
でも、安里歩安彼さんの解答から、nが偶数、奇数のとき、
それぞれ2n, 4nが(F_n)の周期になることが分かりました。
そこで、実はこれらが基本周期であることを以下で示したいと思います。
そのためにまず次のように定義します。

定義2.1. 整数mに対してΡ(m)を次のような集合とする。
Ρ(m)＝{r∈Z| m|F_r}.

このとき次の命題が容易に示されます。

命題2.1. mを整数とする。
(a) Ρ(m)はZの0でないイデアルであり、ある整数ρ(m)＞0により生成される：Ρ(m)＝(ρ(m)).
(b) Ρ(m)⊃Π(m)、すなわち、ρ(m)|π(m).

これを用いると、冒頭の主張が示されます。

定理2.2. 整数n≧4に対して、
　nが偶数ならばπ(F_n)＝2n、
　nが奇数ならばπ(F_n)＝4n.

証明. まず任意の整数n≧3に対して
明らかにρ(F_n)＝nであるから、命題2.1(b)より
n＝ρ(F_n)|π(F_n).
またn≧4ならば、明らかに
F_n−1≠1 (mod F_n)であるから、
π(F_n)≠n.
さらに、安里歩安彼さんが示されたように、nが偶数のとき
π(F_n)|2nであるからπ(F_n)＝2nであり、
nが奇数のときπ(F_n)|4n, π(F_n)≠2nであるから
π(F_n)＝4nである。□

さて、せっかく定義したので、ρ(m)についてもう少し詳しく調べてみたいと思います。
まず前回と同様、次の諸命題が成立します。
（証明も同様なので省略します。）

命題2.3. m,m'を整数とする。
(a) m|m'ならば、Ρ(m)⊃Ρ(m')、すなわち、ρ(m)|ρ(m').
(b) (m,m')＝1ならば、Ρ(mm')＝Ρ(m)∩Ρ(m')、
すなわち、ρ(mm')はρ(m)とρ(m')の最小公倍数。

命題2.4. pを素数、e≧1を整数とし、p≠2またはe≠1とする。
また簡単のためr＝ρ(p^e)とおく。
(a) F_r≡ap^e (mod p^e＋1) (a∈Z) ⇒ F_pr≡ap^e＋1 (mod p^e＋2).
(b) ρ(p^e＋1)＝ρ(p^e)またはpρ(p^e).
(c) ρ(p^e)≠ρ(p^e＋1) ⇒ ρ(p^e＋1)≠ρ(p^e＋2).

系. 奇素数pに対してu≧1をρ(p)＝ρ(p^u)となる最大の整数とすると、
任意の整数e≧uに対してρ(p^e)＝p^e−uρ(p).
特にρ(p)≠ρ(p²)ならば、
　任意の整数e≧1に対して
　ρ(p^e)＝p^e−1ρ(p).
またp＝2のとき、
ρ(2)＝3, ρ(2²)＝6, ρ(2^e)＝3*2^e−2 (e≧3).

また素数p≠5に対して、φ, φ'を前回の解答と同様とするとき、次の命題が成立します。

命題2.5. p≠5を素数とするとき、整数rに対して
r∈Ρ(p) ⇔ (−φ²)^r＝1.
特にρ(p)は−φ²の位数に等しい。

証明. r∈Ρ(p)となるのは、
F_r＝(φ^r−φ'^r)(φ−φ')⁻¹＝0、すなわち、
φ^r＝φ'^rとなることに他ならない。
φ'⁻¹＝−φに注意すれば、主張を得る。□

さらに詳しく調べるため、場合を分けて考えます。

まず(5/p)＝1、すなわち、p≡±1 (mod 5)ならば、
φ∈F_pよりφ^p−1＝1であるから、
(−φ²)^(p−1)/2＝(−1)^(p−1)/2φ^p−1＝(−1/p).
よって命題2.5より、
(−1/p)＝1、すなわち、p≡1 (mod 4)のとき
　ρ(p)|(p−1)/2であり、
(−1/p)＝−1、すなわち、p≡−1(mod 4)のとき
　ρ(p)|p−1, ρ(p)/|(p−1)/2である。

一方(5/p)＝−1、すなわち、p≡±2 (mod 5)ならば、前回の解答で示したように
φ^p＋1＝−1であるから、
(−φ²)^(p＋1)/2＝(−1)^(p＋1)/2φ^p＋1＝(−1/p).
よって命題2.5より、
(−1/p)＝1、すなわち、p≡1 (mod 4)のとき
　ρ(p)|(p＋1)/2であり、
(−1/p)＝−1、すなわち、p≡−1 (mod 4)のとき
　ρ(p)|p＋1, ρ(p)/|(p＋1)/2である。

次にp＝2ならば、−φ²の位数は3であるから、
　命題2.5よりρ(2)＝3.

最後にp＝5ならば、前回の解答で述べたように
F_n＝n3ⁿ⁻¹ (n∈Z)であるから、ρ(5)＝5.

以上の結果をまとめると次のようになります。

定理2.6. 素数pに対して次が成立する。
(a) p＝2ならば、ρ(2)＝3.
(b) p＝5ならば、ρ(5)＝5.
(c) p≡1, 9 (mod 20)ならば、ρ(p)|(p−1)/2.
(d) p≡−1, −9 (mod 20)ならば、
　ρ(p)|p−1, ρ(p)/|(p−1)/2.
　 特にρ(p)≡2 (mod 4).
(e) p≡3, 7 (mod 20)ならば、
　ρ(p)|p＋1, ρ(p)/|(p＋1)/2.
　 特にρ(p)≡0 (mod 4).
(f) p≡−3, −7 (mod 20)ならば、
　ρ(p)|(p＋1)/2.
　 特にρ(p)≡1 (mod 2).

また、素数pに対してπ(p)とρ(p)の関係は次のようになります。

定理2.7. 奇素数pに対して次が成立する。
(a) ρ(p)≡1 (mod 2)ならば、π(p)＝4ρ(p).
(b) ρ(p)≡0 (mod 4)ならば、π(p)＝2ρ(p).
(c) ρ(p)≡2 (mod 4)ならば、π(p)＝ρ(p).

証明. p＝5ならば明らかであるから、p≠5とする。
また簡単のためr＝ρ(p)とおく。
まず命題2.1(b)よりr|π(p)が成立する。
一方、整数kに対してφ^kr＝φ'^krであるから、
F_kr＋1＝(φ^kr＋1−φ'^kr＋1)(φ−φ')⁻¹＝φ^krとなることに注意する。
今、命題2.5より
1＝(−φ²)^r＝(−1)^rφ^2r、
すなわち、F_2r＋1＝φ^2r＝(−1)^rであるから、
rが偶数ならばπ(p)|2rであり、
rが奇数ならばπ(p)|4r, π(p)/|2rであるから、
π(p)＝4rを得る。

さらにrが偶数のとき、rの最小性より
−1＝(−φ²)^r/2＝(−1)^r/2φ^r、
すなわち、F_r＋1＝φ^r＝(−1)^r/2−1であるから、
r≡0 (mod 4)ならばπ(p)|2r, π(p)/|rよりπ(p)＝2rであり、
r≡2 (mod 4)ならばπ(p)|rよりπ(p)＝rである。□

定理2.7より、ρ(p)の具体的な値が求まれば、π(p)は容易に計算されることが分かります。

ところで、奇素数pに対してψ(p)＝p−(5/p)とおけば、
定理2.6よりρ(p)|ψ(p)となりますが、これに関して次のことが知られています：

ψ(p)/ρ(p)はp→∞のとき有界ではないが、
ある正の定数Cが存在してψ(p)/ρ(p)＜C p/log p.

そこで、奇素数pに対してψ(p)/ρ(p)の挙動を調べてみるのは面白いのではないでしょうか。

◆宮城県　アンパンマン さんからの解答。

F_nの剰余の周期をｐとすると
F_p-1=1にならなければなりません。

F_rn≡0 (mod F_n ) ;r＝1,2,3,...

つまりｐ＝kn for some integer k

F_n
＝F₂*F_n-1+F₁*F_n-2
＝F₂(F_n-2+F_n-3)+F₁*F_n-2
＝F₃*F_n-2+F₂*F_n-3
＝　...　
＝F_i+1*F_n-i+F_i*F_n-i-1

F_kn-1
＝F_n+1*F_(k-1)n-1+F_n*F_(k-1)n-2
≡F_n+1*F_(k-1)n-1
≡F_n-1*F_(k-1)n-1 (mod F_n)
≡(F_n-1)^k (mod F_n)

しかし
F_n+1*F_n-1-(F_n)²=(-1)ⁿ

　↓

(F_n-1)²≡(-1)ⁿ (mod F_n).

さらに　
F_n-1 is not congruence to 1 (mod F_n).

よって、

ｐ＝4n, if n=奇数、
ｐ＝2n, if n=偶数。

◆茨城県　小川　康幸 さんからの解答。

フィボナッチ数列を拡張しまして、以下のような数列を考えます。
フィボナッチ数列はx=1 、y=-1のときの特別な場合

U(0)=0 , U(1)=1 , U(n+1)=x*U(n)-y*U(n-1)

また、整数dを、d=x²-4yと定義します。

この数列の自然数mの剰余の周期を考えてみたいと思います。

また、
V(0)=2,V(1)=x,V(n+1)=x*V(n)-y*V(n-1) と言う数列も定義しておきます。

ここに出てくる式や定理は、共立出版「素数の世界」 Paulo Ribenboim著 から証明なしで引用しているものがたくさんあります。

例えば、
U(s+t)=U(s+1)*U(t)-y*U(s)*U(t-1)
s≧tのとき、U(s+t)=U(s)*V(t)-y^t*U(s-t)
U(s+1)V(s)-U(s)V(s+1)=2*y^s

pがdの約数ではないとき、そして、(d/p)=1 のとき、
π(p)はp-1の約数、λ(p)=0になる。

そして、(d/p)=-1 のとき、fをy^f≡1 (mod p)となる最小の自然数とすると、
π(p)は(p+1)*fの約数、λ(p)=0になる。
当然、fは(p-1)の約数なので、π(p)は、p²-1の約数である。

pがdの約数となるとき、U(p)≡0 (mod p)となること。

U(s)がp^tで割り切れるとき、U(p*s)はp^t+1で割り切れる。

p≧3またはt≧2のとき、U(s)がp^tで割り切れて、p^t+1で割り切れない
⇒U(s)がp^t+1で割り切れて、p^t+2で割り切れない

U(n)が、n≧n₀ (n₀は０以上の自然数とする) を満たす任意の整数nで、
U(n+k)≡U(n) (mod m) となる、自然数kが存在するとき、kを広義の周期と呼ぶ事にします。
n₀=0のときは、普通の周期と同じです。

上記のような、n₀とkの取り方はいろいろあるが、
kの値が最小になるように、n₀とkの値を選ぶ。
このときの、n₀、kの値をn₀=λ(m)，k=π(m)と書くことにする。

【命題１ 】

n≧n₁ (n₁は０以上の自然数とする) を満たす任意の整数nで、
U(n+g)≡U(n) (mod m) となる、自然数gが存在するとき、
gは、π(m)で割り切れる。

【証明 】

gがπ(m)で割り切れないと仮定すると、
g=π(m)*q+r 0＜r＜π(m)

n≧n₀ (n₀は０以上の自然数とする) を満たす任意の整数nで、
U(n+π(m))≡U(n) (mod m)となる。

よって、n≧max{n₀,n₁}となる、任意の自然数nで、
U(n+π(m))≡U(n) (mod m)、U(n+g)≡U(n) (mod m) とかける。

U(n+g)
≡U(n+π(m)*q+r)
≡U(n+π(m)*(q-1)+r)
≡U(n+π(m)*(q-2)+r)
≡･･･
≡U(n+r)
≡U(n) (mod m)

これは、π(m)の仮定に反する。

証明終

【命題２】

1．

a'をaの約数とする。
π(a')は、π(a)の約数、λ(a')≧λ(a)である。

【証明 】

n≧λ(a)を満たす任意の整数nで、U(n+π(a))≡U(n) (mod a)となる。
よって、U(n+π(a))≡U(n) (mod a')とかける。
よって、命題1より、π(a')は、π(a)の約数である。

2．

aとbを互いに素な自然数とする。
π(a*b)はπ(a)とπ(b)の最小公倍数、
λ(a*b)=max{λ(a),λ(b)}である。

【証明 】

1．より、π(a)とπ(b)は、π(a*b)の約数、
よって、π(a*b)は、π(a)とπ(b)の最小公倍数で割り切れる。

また、1．より、λ(a*b)≧λ(a),λ(b)
よって、λ(a*b)≧max{λ(a),λ(b)}

逆に、π(a)とπ(b)の最小公倍数をlとおくと、
n≧λ(a) を満たす任意の整数nで、U(n+l)≡U(n) (mod a)となる。
n≧λ(b) を満たす任意の整数nで、U(n+l)≡U(n) (mod b)となる。

よって、n≧max{λ(a),λ(b)}となる、任意の自然数nで、
U(n+l)≡U(n) (mod a*b)とかける。

よって、λ(a*b)≦max{λ(a),λ(b)}

よって、命題1より、lはπ(a*b)で割り切れる。

よって、π(a*b)はπ(a)とπ(b)の最小公倍数である。
そして、λ(a*b)=max{λ(a),λ(b)}である。

終

命題2の2．より、mとしては、素数の冪だけを考えればよい事が分かる。
(m=p^eとして考える)

【命題３ 】

pがyの約数のとき、xがpで割り切れるとき、
λ(p^e)≦e²+e ,π(p^e)=1

xがpで割り切れないとき、
λ(p^e)≦e, π(p^e)は、eがpで割り切れないとき、
p^e-1*(p-1)の約数、

eがpで割り切れるとき、π(p^e)は、p^e*(p-1)の約数

【証明】

s≧tのとき、U(s+t)=U(s)*V(t)-y^t*U(s-t) だから、
U(s+e)≡U(s)*V(e) (mod p^e)

V(n)=x*V(n-1)-y*V(n-2)≡x*V(n-1) (mod p)
ゆえに、V(n)≡xⁿ (mod p)

x≡0 (mod p) のとき、V(e)≡0 (mod p)

n≧e²+eなる任意の整数nに対して、

U(n)
≡U(n-e)*V(e)
≡U(n-2e)*{V(e)}²
≡･･･
≡U(n-e²)*{V(e)}^e
≡0 (mod p^e)

よって、π(p^e)=1

xがpで割り切れないとき、V(e)もpで割り切れない。

n≧eなる任意の整数nに対して、

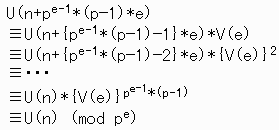
よって、π(p^e)は、p^e-1*(p-1)*eの約数。

同様に、π(p^e+1)は、p^e*(p-1)*(e+1)の約数。

命題2の1.より、π(p^e)は、p^e*(p-1)*(e+1)の約数でもある。

(e+1)*p≡p (mod e)だから、ユークリッドの互除法の証明と同様にして、
(e+1)*pとeの最大公約数=pとeの最大公約数が分かるから、

p^e*(p-1)*(e+1)とp^e-1*(p-1)*eの最大公約数は、
eがpで割り切れないとき、eと(e+1)*pは互いに素だから、
p^e-1*(p-1)

また、eがpで割り切れるとき、eと(e+1)*pの最大公約数はpだから、
p^e*(p-1)

よって、π(p^e)は、eがpで割り切れないときp^e-1*(p-1)の約数、
eがpで割り切れるときp^e*(p-1)の約数であることがわかる。

終

yがpで割り切れないとき（このとき、λ(p)=0となる）

【命題４】

pが奇数のときπ(p)を求める。

【証明】

pがdの約数ではないとき、そして、(d/p)=1 のとき、
π(p)はp-1の約数、λ(p)=0になる。

そして、(d/p)=-1 のとき、fをy^f≡1 (mod p)となる最小の自然数とすると、
π(p)は(p+1)*fの約数、λ(p)=0になる。

当然、fは(p-1)の約数なので、π(p)は、p²-1の約数である。

そして、pがdの約数となるとき、U(p)≡0 (mod p)

U(p+1)≡0 (mod p)となると仮定する。
U(p+1)V(p)-U(p)V(p+1)=2*y^p

2*y^p≡0 (mod p)となる。
pは奇数より、y^p≡0 (mod p)
よって、y≡0 (mod p)となって不合理

U(s+t)=U(s+1)*U(t)-yU(s)*U(t-1)だから、
U(p*(p-1)+n)
≡U(p+1)*U(p*(p-2)+n)-yU(p)*U(p*(p-2)+n-1)
≡U(p+1)*U(p*(p-2)+n)
≡U(p+1)*[U(p+1)*U(p*(p-3)+n)-yU(p)*U(p*(p-3)+n-1)]
≡{U(p+1)}²*U(p*(p-3)+n)
≡･･･
≡{U(p+1)}^p-1*U(n) (mod p)

よって、U(p*(p-1)+n)≡U(n) (mod p)
ちなみに、λ(p)=0である。

よって、π(p)はp*(p-1)の約数である。

終

【命題５】

π(p^e)=p^e-e'π(p)
ただし、e'は、π(p^e')=π(p)となる、最大の整数とする。

また、このとき、λ(p^e)=0

【証明 】

U(1+π(p^e))≡1 (mod p^e) ,
U(π(p^e))≡0 (mod p^e) ,
λ(p^e)=0と仮定すると

U(p*π(p^e))≡0 (mod p^e+1),

U(1+p*π(p^e))
≡U(1+π(p^e))*U(1+(p-1)*π(p^e))-yU(π(p^e))*U((p-1)*π(p^e))
≡U(1+π(p^e))*U(1+(p-1)*π(p^e))
≡{U(1+π(p^e))}²*U(1+(p-2)*π(p^e))
≡･･･
≡{U(1+π(p^e))}^p
≡(1+p^e*K)^p
≡1+p^e+1*K+p^e+2*L
≡1 (mod p^e+1 )

よって、任意の0以上の整数 nに対して、

U(n+p*π(p^e))
≡U(1+p*π(p^e))*U(n)-yU(p*π(p^e))*U(n-1)
≡U(n) (mod p^e+1)

よって、命題1より、π(p^e+1)はp*π(p^e)の約数である。

またこれより、λ(p^e+1)=0

π(p^e)はπ(p^e+1)の約数だから、
π(p^e+1)=p*π(p^e)またはπ(p^e)

ここで、π(p^e+1)≠π(p^e) ならば、
π(p^e+2)≠π(p^e+1) である事を示す。

U(π(p^e))がp^e+1で割り切れないとき、
U(p*π(p^e))は、p^e+1で割り切れるが、p^e+2では割り切れない。

よって、π(p^e+2)≠π(p^e+1) である。

そして、U(π(p^e))がp^e+1で割り切れるとき、
U(1+π(p^e))-1は、p^eで割り切れるが、p^e+1で割り切れない。

もし割り切れるとすると、任意の0以上の整数nに対して、

U(n+π(p^e))
≡U(1+π(p^e))*U(n)-yU(π(p^e))*U(n-1)
≡U(n) (mod p^e+1)

となって、π(p^e+1)≠π(p^e)に反する。

U(1+π(p^e))=1+p^e*K
Kはpで割り切れない整数とかける。

mod p^e+2で、

U(1+pπ(p^e))
≡U(1+π(p^e))*U(1+(p-1)*π(p^e))-yU(π(p^e))*U((p-1)*π(p^e))
≡U(1+π(p^e))*U(1+(p-1)*π(p^e))
≡{U(1+π(p^e))}²*U(1+(p-2)*π(p^e))
≡･･･
≡{U(1+π(p^e))}^p
≡(1+p^e*K)^p
≡1+p^e+1*K+p^e+2*L
≡1+p^e+1*K (mod p^e+2 )

よって、U(1+pπ(p^e))-1は、
p^e+1で割り切れるが、p^e+2で割り切れない。

よって、π(p^e+2)≠π(p^e+1) である。

このことより、π(p^e+1)=p*π(p^e)ならば、
π(p^e+2)=p*π(p^e+1)

よって、e'をπ(p^e')=π(p)となる、最大の整数とすると、
π(p^e)=p^e-e'π(p)

また、このとき、λ(p^e)=0

xが偶数のとき(このときyは奇数である)、λ(2)=0、π(2)=2
xが奇数のとき、λ(2)=0、π(2)=3

【命題６】

π(4)=π(2)のとき、π(2^e)=2^e-e'π(2)
ただし、e'は、π(2^e')=π(2)となる、最大の整数とする。
また、このとき、λ(2^e)=0

π(4)≠π(2)のとき、
xが偶数のとき、π(2^e)=2^e
xが奇数のとき、π(2)=3,π(2^e)=3*2^e-e''+1
ただし、e≧2かつ、e''は、π(2^e'')=π(4)となる、最大の整数とする。
また、このとき、λ(2^e)=0

【証明 】

U(1+π(2^e))≡1 (mod 2^e) ,
U(π(2^e))≡0 (mod 2^e) ,
λ(2^e)=0と仮定すると

命題5と同様にして、
U(1+2π(2^e))≡1 (mod 2^e) ,
U(2π(2^e))≡0 (mod 2^e) ,
λ(2^e+1)=0　が分かる。

ゆえに命題5と同様にして、
π(2^e+1)=2*π(2^e)またはπ(2^e)

π(4)=π(2)のとき、e≧2と考えてよい

ここで、π(2^e+1)≠π(2^e) ならば、
π(2^e+2)≠π(2^e+1) である事を示す。

U(π(2^e))が2^e+1で割り切れないとき、
U(2*π(2^e))は、2^e+1で割り切れるが、2^e+2では割り切れない。

よって、π(2^e+2)≠π(2^e+1) である。

そして、U(π(2^e))が2^e+1で割り切れるとき、命題5の証明と同様にして、
U(1+π(2^e))-1は、
2^eで割り切れるが、2^e+1で割り切れない事が分かる。

U(1+π(2^e))=1+2^e*K Kは2で割り切れない整数とかける。

mod 2^e+2で、

U(1+2π(2^e))
≡U(1+π(2^e))*U(1+π(2^e))-yU(π(2^e))*U(π(2^e))
≡･･･
≡{U(1+π(2^e))}²
≡(1+2^e*K)²
≡1+2^e+1*K+2^e+2*L
≡1+2^e+1*K (mod 2^e+2 )

よって、U(1+2*π(p^e))-1は、
2^e+1で割り切れるが、2^e+2で割り切れない。

よって、π(2^e+2)≠π(2^e+1) である。

このことより、
π(2^e+1)=2*π(2^e)ならば、
π(2^e+2)=2*π(2^e+1)

π(4)≠π(2)のとき、π(4)=2*π(2)である。

xが偶数のとき、 yは奇数だから、V(2)=x²-2*y≡2 (mod 4)

U(4)=U(2)*V(2)だから、U(4)は4で割り切れて、8で割り切れない。

π(4)=4だから、U(π(4))は4で割り切れて、8で割り切れない。

よって、π(8)≠π(4)がわかる。

以下π(4)=π(2)のときの証明と同様にして、
π(2^e+1)=2*π(2^e)ならば、
π(2^e+2)=2*π(2^e+1)が示される。

よって、π(2^e)=2^e

xが奇数のとき、V(3)=x³-3y≡1-3*1≡0 (mod 2)

U(6)=U(3)*V(3)より、U(6)は4で割り切れる。

以下π(4)=π(2)のときの証明と同様にして、e≧2のとき、
π(2^e+1)=2*π(2^e)ならば、
π(2^e+2)=2*π(2^e+1)が示される。

よって、π(2^e)=2^e-e''π(4)=2^e-e''+1*3

終

因みに、π(4)=π(2)⇔U(π(2))が4で割り切れる。

xが偶数のとき、U(π(2))=x 、
xが奇数のときU(π(2))=x²-yだから、

(4)=π(2)⇔xが偶数のとき、xが4で割り切れる。
xが奇数のとき、x²≡1 (mod 4)だから y≡1 (mod 4)

長くなりましたが、まとめると、
命題2.2より、mを、m=Π(p_i)^e_iと書くとき、

λ(m)=λ((p_i)^e_i)の最大値、π(m)=π((p_i)^e_i)の最小公倍数

pがyの約数のとき、命題3より、xがpで割り切れるとき、
λ(p^(e))≦e²+e ,π(p^e)=1

xがpで割り切れないとき、λ(p^e)≦e, π(p^e)は、
eがpで割り切れないとき、p^e-1*(p-1)の約数、

eがpで割り切れるとき、π(p^e)は、p^e*(p-1)の約数

pが奇数でpがyの約数ではないとき、
命題4よりpがdの約数ではないとき、そして、(d/p)=1 のとき、
π(p)はp-1の約数、λ(p)=0になる。

そして、(d/p)=-1 のとき、λ(p)=0になる。
π(p)は、p²-1の約数である。

pがdの約数となるとき、π(p)はp*(p-1)の約数である。
λ(p)=0になる。

命題5より、π(p^e)=p^e-e'π(p)
ただし、e'は、π(p^e')=π(p)となる、最大の整数とする。

また、このとき、λ(p^e)=0

yが奇数のとき

命題6より、xが偶数のとき、x≡0 (mod 4)。
xが奇数のとき、y≡1 (mod 4)となるとき、

π(2^e)=2^e-e'π(2)
ただし、e'は、π(2^e')=π(2)となる、最大の整数とする。

また、このとき、λ(2^e)=0

xが偶数のとき、x≡2 (mod 4)。
xが奇数のとき、y≡3 (mod 4)となるとき、

xが偶数のとき、π(2^e)=2^e
xが奇数のとき、π(2)=3,π(2^e)=3*2^e-e''+1

ただし、e≧2かつ、e''は、π(2^e'')=π(4)となる、最大の整数とする。
また、このとき、λ(2^e)=0

　『フィボナッチ数列の性質 Part3』へ

　数学の部屋へもどる