『フィボナッチ数列の性質』解答

◆広島県　清川　育男　さんからの解答。

【問題２】

　ｎが４の倍数のとき。

【問題３】

Ｆ_4nが３の倍数の証明。

数学的帰納法による。
ｎ＝１，Ｆ₄＝３。
これは３の倍数。

ｎ＝ｋ，Ｆ_4kが３の倍数とする。
フィボナッチ数列の定義により

５×Ｆ_4k＋３×Ｆ_4k-1＝Ｆ_4(k+1)

左辺は３の倍数である。
よってｎ＝ｋ＋１のときも成り立つ。
したがって,Ｆ_4nは３の倍数である。

以上です。
これで数学的帰納法になっているのでしょうか。　

【コメント】

　証明はＯＫだと思います。
説明不足だったのですが、問題は、「フィボナッチ数が３の倍数」である必要十分条件は「ｎが４の倍数」であることの証明です。
ですからｎが４の倍数に限ることも証明してください。

◆広島県　清川　育男　さんからの解答。

【問題３】

　十分条件は証明済み。

（続き）必要条件　ｎが４の倍数以外にはＦ_nが３の倍数にならないことの証明。

ｎを４による剰余に分類して、背理法を使って証明する。

（１）ｎ＝４ｋ＋１のとき Ｆ_4k+1が３の倍数と仮定する。
Ｆ_4k+1＝Ｆ_4k＋Ｆ_4k-1
Ｆ_4k+1，Ｆ_4kは３の倍数であるから、Ｆ_4k-1も３の倍数となる。
以下、論を進めると全てのフィボナッチ数が３の倍数となる。
これは矛盾である。
これは、Ｆ_4k+1を３の倍数と仮定としたことによる。
したがって、ｎ＝４ｋ＋１のとき Ｆ_4k+1は３の倍数とならない。

（２）ｎ＝４ｋ＋２，Ｆ_4k+2
（３）ｎ＝４ｋ＋３，Ｆ_4k+3

（２），（３）のとき同様の論法により、
ｎ＝４ｋ＋２の時Ｆ_4k+2、ｎ＝４ｋ＋３のときＦ_4k+3はそれぞれ３の倍数とならない。
したがってＦ_nが３の倍数となるための必要十分条件はｎが４の倍数である。

【コメント】

今度はＯＫです。
４の剰余で分類したところが、定石とはいえ、なかなか巧妙ですね。

◆広島県　清川　育男　さんからの解答。

【問題４】

補題１《ｎが素数（２は除く）のとき、ｎ＋１，ｎ−１は素数ではない。》

証明
ｎが素数（２は除く）であれば少なくともｎは奇数である。
したがってｎ＋１，ｎ−１は偶数であるからそれぞれは素数ではない。

補題２《Ｆ_n+1，Ｆ_n-1は互いに素である。》

証明　背理法による。
仮定．Ｆ_n+1，Ｆ_n-1は互いに素でないとする。
Ｆ_n+1，Ｆ_n-1の最大公約数をａとする。（ａ＜＞１）
Ｆ_n+1＝ａ×ｂ，Ｆ_n-1＝ａ×ｃとする。（ｂ＞ｃ＞１）
Ｆ_n+1＝Ｆ_n+Ｆ_n-1であるから、
ａ×ｂ＝Ｆ_n＋ａ×ｃ
両辺をａで割ると、
ｂ＝Ｆ_n/ａ+ｃ，Ｆ_n/ａ＝ｂ−ｃ
Ｆ_n（フィボナッチ数）は自然数であるからａの倍数である。
Ｆ_n+1,Ｆ_n，Ｆ_n-1はａの公約数を持つことになる。
これは矛盾である。
この矛盾は、仮定に起因する。
したがって、Ｆ_n+1，Ｆ_n-1は互いに素である。

補題３《Ｆ_n+1，Ｆ_n，Ｆ_n-1は１以外の公約数を持たない。》

証明は補題２に準ずる。

補題１、補題２、補題３を使って本題を証明する。

１）　背理法による。
　仮定．ｎが素数（２は除く）のとき、Ｆ_nは素数ではない。
　Ｆ_n＝ｐ×ｑ，Ｆ_n+1＝ａ，Ｆ_n-1＝ｃとする。
　ａ＞ｐ×ｑ＞ｃ＞ｐ＞ｑ＞１とする。
　フィボナッチ数列の定義より、
　ａ＝（ｐ×ｑ）+ｃ
　ｐ＝（ａ−ｃ）／ｑ
　ｐは自然数であるから、
　ｐ＝ｍ／ｑ.................1）
　ｍはｍ>1の自然数とする。
　ｍ＝ａ−ｃ.................2）
　フィボナッチ数列の定義より、
　ａ＝ｍ＋ｃ.................3）
　ｍ＝ｐ×ｑ.................4）
　ｍを1）に代入すると、
　ｐ＝（ｐ×ｑ）×ｑ
　ｑ²＝１，ｑ＝１
　ｑ＝1は矛盾である。
　これは仮定に起因する。
　したがって、ｎが素数（２は除く）のとき、Ｆ_nは素数である。

２）ｎ＝４のときＦ₄＝３
　これは素数である。

以上です。
フィボナッチの数列の一般項は、

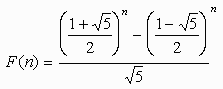
　この一般項から次々に素数が生成されることになりますが、このアルゴリズムでは現在までに知られている最大の素数を越えることは無理なのでしょうね。
しかし確実に素数を発見できますね。

【コメント】

　この証明も正しいと思います。
ただし、証明すべき事は、「フィボナッチ数が素数であるとすると、「ｎ＝４またはｎ自身も素数」のいずれかになる」ですから、今の証明は逆になっています。
「ｎ＝４またはｎ自身も素数」以外の場合は、フィボナッチ数は素数でないことを証明してください。

◆神奈川県　わかさひ君からの解答。

【問題４】

Ｆn＝　Ｆn-1＋ Ｆn-2
   ＝２Ｆn-2＋ Ｆn-3
   ＝３Ｆn-3＋ ２Ｆn-4
   ＝５Ｆn-4＋ ３Ｆn-5
   ＝８Ｆn-5＋ ５Ｆn-6

ここから予測される事実は、
Ｆ_nを、隣り合う二つのフィボナッチ数の一次結合で表すとき係数がフィボナッチ数列になる
である。

式で表すと次のようになる。
Ｆ_m+n＝Ｆ_m+1Ｆ_n + Ｆ_mＦ_n-1

実際、これはＦ_nの一般式
　Ｆ_n＝ (φⁿ−(−1/φ)ⁿ )／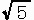

を代入して計算すると成り立つことが確認できる。
(ただしφは黄金比 (１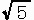＋)／２ )

ここで、合成数 ｎ が、ｎ＝ｐｑ という２数ｐ，ｑの積で表されるとき、
Ｆ_pq＝Ｆ_(p-1)q+q＝Ｆ_(p-1)q+1Ｆ_q＋Ｆ_(p-1)qＦ_q-1
である。

同様に ｃ＝２， ...， ｐ に対して
Ｆ_cq＝Ｆ_(c-1)q+1Ｆ_q＋Ｆ_(c-1)qＦ_q-1 ...(*)

であり、特に

Ｆ_2q＝Ｆ_q+1Ｆ_q＋Ｆ_qＦ_q-1＝Ｆ_q(Ｆ_q+1＋Ｆ_q-1) ...(**)

である。

(*)式の右辺第１項はＦ_qの倍数になっており、第２項も、(**)式より帰納的にＦ_qの倍数になることが分かる。

したがって、Ｆ_pqは Ｆ_qの倍数になる。

フィボナッチ数列は、 Ｆ₁＝ Ｆ₂＝１
ｎ≧３では Ｆ_n> 1 であるから、
ｐ，ｑいずれかが２よりも大きければ、 Ｆ_q>１となる。
このとき、Ｆ_qがＦ_nの約数であることより、Ｆ_nは素数とならないことになる。

また、ｐ＝ｑ＝２のとき、Ｆ_p＝Ｆ_q＝１となるので、別に考えなければなりません。
Ｆ₄＝３は素数なので、ｎ＝４は、ｎが合成数のとき唯一例外的にフィボナッチ数 Ｆ_nが素数になる。

以上をまとめると、
　ｎが合成数で、かつ４でなければ、Ｆ_nは合成数となる。
(証明おしまい)

なお、フィボナッチ数列が無限に素数になることがあるかどうかは分かっていません。
もちろん、上記の結果より、フィボナッチ数が素数であるなら、それは素数番目の項にしか現れることはありませんね。

◆東京都の中学校１年生　安里歩安彼　さんからの解答。

【問題１】

１〜ｎ−１までは命題が示されているとして、帰納法で示そう。

任意の自然数ｎに関して、
Ｆ_mが、ｎ/２より大きくなるようなｍが存在することは、容易に分かる。

ｎ−Ｆ_m＝ｋは、帰納法の仮定より、相異なるフィボナッチ数列の数の和で表現できるので、
またｋ＜Ｆ_mより、それらのフィボナッチ数列の中にＦ_mが含まれることはないので、示される。

【問題２，３】

●Prop1,1
Ｆ_nが３の倍数⇔ｎが４の倍数

証明：

Ｆ₁〜Ｆ₈の、mod ３での表示は、

１１２０２２１０となり、Ｆ₉以降もこれと同じようになることは、最後から２番目の項が１となることより明らか。

よって、示される

【問題４】

Prop1,1の自然な拡張として、以下のProp1,2がいえる。

●Prop1,2

Ｆ_nがＦ_mの倍数⇔ｎがｍの倍数

証明も、Prop1,1とほぼ同様にできるので省略する。

さて、Prop1,２より、Ｆ_n＝ｐが素数なら、その約数はｐか１なので、ｎは１，２，ｎでしか割り切れない。
よってｎがｐのときはよい。

また、ｎがｐでなければ、ｎ＝４であることは、
ｎ＞４なら、ｎ/２＞２より分かる。

よって示された。

最後に…僕からの挑戦問題！！

フィボナッチ数列の数Ｆ_nの２乗Ｆ_n×Ｆ_nの倍数である、
最小のフィボナッチ数列の数をＦ_mとするとき、ｍを求めよ。

◆広島県　清川　育男　さんからの解答。

【問題５】

証明はできないのですが、推理しました。

n=1 F(1)*F(1)=1                F(1)=F(1*1)=F(1*F(1))
n=2 F(2)*F(2)=1                F(2)=F(2*1)=F(2*F(2))
n=3 F(3)*F(3)=2*2=4            F(6)=F(3*2)=F(3*F(3))
n=4 F(4)*F(4)=3*3=9            F(12)=F(4*3)=F(4*F(4))
n=5 F(5)*F(5)=5*5=25           F(25)=F(5*5)=F(5*F(5))
n=6 F(6)*F(6)=8*8=64           F(48)=F(6*8)=F(6*F(6))
n=7 F(7)*F(7)=13*13=169        F(91)=F(7*13)=F(7*F(7))
n=8 F(8)*F(8)=21*21=441        F(168)=F(8*21)=F(8*F(8))
n=9 F(9)*F(9)=34*34=1156       F(306)=F(9*34)=F(9*F(9))
    ...................................................
　F(n)*F(n) .............................. F(n*F(n))
 
   m=n*F(n)
   F(n)*F(n)|F(m)

◆東京都　ヒロキ　さんからの解答。

【問題１】

数学的帰納法による

n = 3 のとき
Ｆ_n = 2 以下の自然数は

1 = Ｆ₁ = Ｆ2
2 = Ｆ₃ = Ｆ₁ + Ｆ₂

となり相異なるフィボナッチ数の和で表すことができる

n = k のとき
Ｆ_k 以下のすべての自然数が相異なるフィボナッチ数の和で表すことができるとする

n = k + 1 のとき
フィボナッチ数の定義より

Ｆ_k+1 = Ｆ_k + Ｆ_k-1 (1)
Ｆ_k ＞Ｆ_k-1 (2)

(2)よりＦ_k-1までの自然数をフィボナッチ数の和で表した場合、
Ｆ_kが含まれないのは明らか

よって仮定および(1)(2)より
Ｆ_k ＜ Ｎ ≦ Ｆ_k+1 なるすべての自然数Ｎもまた相異なるフィボナッチ数の和で表すことができる

したがって n = k + 1 のときも成り立つ
よって題意は証明された。

◆広島県　清川　育男　さんからの解答。

【問題５】

補題

任意のa,bについて
F(a) | F(a*b)
証明略。

題意を満たすmが存在するとすれば、
k*F(n)*F(n)=F(m) ...........(1)

最小のkということは最小のmと同値である。
なぜなら、F(m)≦F(m+1) であるから。
F(m)は合成数であるから、mも合成数でなければならない。

また、少なくともF(n)で割り切れなければならないので、
m=n*m1　の形でなければならない。

k*F(n)*F(n)=F(n*m1)　 ...........(2)

一方、F(m1) | F(n*m1)であるから、
F(m1) | k*F(n)*F(n)　である。

したがって最小のmは、m1=F(n)
よって、m=n*F(n)

(1)式の存在の証明ができません。残念、、、。
mの存在証明をお願いします。

◆茨城県　小川　康幸　さんからの解答。

【問題５】

フィボナッチ数列を拡張して、次のような数列を考える。

U₀=0、U₁=1
U_n+2=x*U_n+1-y*U_n
ただし、xとyは互いに素とする。

便利のため、V₀=2 , V₁=x
V_n+2=x*V_n+1-y*V_nと言う数列を考える。

この数列に対して、(U_n)^wがU_mを割り切るような、最小の自然数mを求める。

また、整数dをd=x²-4*yと定義する。
U_n≡0 (mod m)となる最小のnをn=ρ(m)とかく事にする。

このとき、求める問題は、ρ{(U_n)^w}を求める事に他ならない。

ここで、次の命題が成り立つ。

命題１

mがyと互いに素の時、U_sがρ(m)で割り切れるとき、sはρ(m)で割り切れる。

命題２

aとbをyと互いに素な自然数とする。
aとbが互いに素のとき、ρ(a*b)=ρ(a)とρ(b)の最小公倍数

命題３

dが素数pで割り切れるとき、ρ(p)=p

命題４

yが奇素数pで割り切れないとき、ρ(p^e)=p^e-e'*ρ(p)
ただし、e'は、ρ(p^e')=ρ(p)となる最大の自然数。

命題５

yが奇数、
そしてρ(4)=ρ(2)のとき、ρ(2^e)=2^e-e'*ρ(2)
ただし、e'は、ρ(2^e')=ρ(2)となる最大の自然数。

yが奇数、そしてρ(4)≠ρ(2)のとき、xが偶数のとき、
ρ(2^e)=2^e

命題６

nがyと互いに素のとき、U_nがnで割り切れる。⇔pを任意のnの素因数とするとき、ρ(p)がnで割り切れる。

命題１から６までの証明は、『フィボナッチ数列の性質 Part2』の私の解答にあります。

命題７の証明に、次の公式を使います。

nが奇数のとき、

2^n-1*U_n=n*x^n-1-_nC₃*x^n-3*d+・・・±d^(n-1)/2

使用した公式集（Paulo Riebenboim著 共立出版「素数の世界」）

命題７

pを3以上の素数とする。

yがpで割り切れず、dがp²で割り切れるとき、U_pはpで割り切れるが、p²で割り切れない。
つまり、pが3以上の素数で、かつ、dがp²で割り切れるとき、
ρ(p^e)=p^e

証明

2^p-1*U_p
＝p*x^p-1-_pC₃*x^p-3*d+・・・±d^(p-1)/2
≡0 (mod p)

ゆえに、U_p≡0 (mod p)

U_pがp²で割り切れると仮定すると、

0≡2^p-1*U_p
　≡p*x^p-1-_pC₃*x^p-3*d+・・・±d^(p-1)/2
　≡p*x^p-1 (mod p²)

x^p-1≡0 (mod p) よって、x≡0 (mod p)
4y≡x²-d≡0 (mod p) よって y≡0 (mod p)

これは、xとyが互いに素であることに反する。

U_pはp²で割り切れない。

よって、このとき、命題４のe'は1だから、
命題４より、ρ(p^e)=p^e

証明終

命題８

任意の自然数nに対して、U_nとyは互いに素である。

証明

U_nとyが共通の素因数qを持つと仮定する。

0≡U_n
　≡x*U_n-1-y*U_n-2
　≡x*U_n-1
　≡x²*U_n-2
　≡・・・
　≡x^n-1 (mod q)

よってx≡0となって、xとyが公約数qを持つ事になって不合理

証明終

R₀=0、R₁=1
R_l+2=V_n*R_l+1-yⁿ*R_lなる数列 R_lを考える。

整数eを、e=V_n²-4*yⁿと定義する。

そして、R_g≡0 (mod h)となる自然数gのうち最小のものを、g=θ(h)とかく事にする。

命題９

任意の自然数nに対して、V_nとyⁿは互いに素である。

証明

V_nとyⁿが、共通の素因数qを持つと仮定する。
qはyの約数である。
よって

　0
≡V_n
≡x*V_n-1-y*V_n-2
≡x*V_n-1
≡x²*V_n-2
≡・・・
≡xⁿ (mod q)

x≡0 (mod q)となって、xとyが互いに素であることに反する。

証明終

命題１０

証明

U_nは、zの2次方程式、z²-x*z+y=0の相異なる2つの解をα、βとすると

Un=

αn-βn α-β

、Vn=α2+β2

そして、Rl=

αl*n-βl*n α-β

と書ける。

U_nでのdに対応するR_lの値eは、
e=(V_n)²-4*yⁿ=(αⁿ-βⁿ)²=d*(U_n)²である。

(U_n)^w-1の任意の素因数をpとすると、pは、U_nの素因数だから、
e=V_n²-4*yⁿ=d*(U_n)²はp²で割り切れる。

また、(U_n)^w-1はyⁿと互いに素
（命題８より、pとU_nは互いに素だから）

また、命題９より、V_nとyⁿも互いに素であるから、
R_lもU_nと同様に、命題１〜８が成立する。

命題３より、θ(p)=p

θ(p)は、(U_n)^w-1の約数だから、命題６より、
は、(U_n)^w-1で割り切れる。

よって、命題１０は示された。

証明終

命題１１

U_Mが(U_n)^wで割り切れるような最小のMについて、

証明

U_Mは少なくとも、U_nで割り切れる。

Mは命題１よりρ(U_n)=nで割り切れる。
M=n*L

U_M=R_l*U_n

R_lが{U_n}^w-1で割り切れなければならない。

(U_n)^w-1の任意の素因数をp、そして、指数をsとする。

命題２よりθ[(U_n)^w-1]=pが
(U_n)^w-1の任意の素因数を動くときのθ(p^s)の最小公倍数
e=(V_n)²-4*yⁿ=d*(U_n)²だから、eは、p²で割り切れる。

命題７より、p≧3のとき、θ(p^s)=p^s

ところが、p=2のときは、命題４と命題５より

θ(2^s)=2^s-s'+1となる。
ただし、s'はθ{p^s'}=θ(p)となる最大の自然数

よって、U_nが2と互いに素のとき。
θ({U_n}^w-1)=(U_n)^w-1

よって、M=θ({U_n}^w)=(U_n)^w-1*nであることが分かる。

U_nが2で割り切れるとき、
R₂=V_nが、4で割り切れないとき、
命題５より、上と同様に
M=θ({U_n}^w)=(U_n)^w-1*nであることがわかる。

また、w=1かつ、U_nが4で割り切れないときも、
M=θ(U_n)=U_n*n
が成立する。

そうでないときは、
θ({U_n}^w)＜(U_n)^w-1*n
となることがある。

正確には、

M=θ({Un}w)＝

(Un)w-1*n 2s'-1

となる。

ただし、s'はθ(2)=θ(2^s')となる最大の自然数とする。

解答終

◆愛知県　Y.M.Ojisan さんからの解答。

【問題５】

∵　フィボナッチの基本です。

＜定義と補題２＞

Ｇ_N＝Ｆ_N+1+Ｆ_N-1＝（α^N＋β^N）

∵　　略。補題１を代入すればよい。

＜補題３＞

Ｆ_N^２−Ｆ_N+KＦ_N-K＝(−１)^N+KＦ_K^２

∵　補題１を左辺に代入します。

(α−β)^２×左辺
＝(α^N−β^N)^２−(α^N+K−β^N+K)(α^N-K−β^N-K)

＝(−１)N{−２＋

(

α β

)

K

＋

(

β α

)

K

}

＝(−１)^N+K｛−２(αβ)^K＋(α)^2K＋(β) ^2K｝
＝(−１)^N+K(α^K−β^K) ^２
＝(−１)^N+K(α−β)^２×Ｆ_K^２

＜補題４＞

Ｆ_KN＝G_NＦ_N(K-1)−(−１)^NＦ_N(K-2)
（Ｎ飛びフィボナッチの漸化式　）

∵　数学的帰納法で簡単に証明可能。略

＜補題５＞

Ｈ_N、K≡Ｆ_N-3×Ｈ_N、K-1−(−１)^NＨ_N、K-2　(mod Ｆ_N)
Ｈ_N、0＝２　、Ｈ_N、1＝Ｆ_N-3で定義される数列の周期は４である。

略記として　今後<N> は演算子または符号でＮが偶数のとき＋、奇数のとき−とする。

∵　補題２においてＫ＝３(Ｎ−３)→Ｎ　とすると、Ｆ₃＝２なので
Ｆ_N-3^２−Ｆ_NＦ_N-6＝<N>Ｆ₃^２＝<N>４　　である。従って
Ｆ_N-3^２≡<N>４　　(mod Ｆ_N)

Ｈ₂　〜　Ｈ_５を計算すると、下記のようにＨは周期４である。
絶対値は周期２。

Ｈ₂＝Ｆ_N-3×Ｆ_N-3−<N>２≡<N>２　(mod Ｆ_N)

Ｈ₃＝Ｆ_N-3×(<N>２)−(<N>Ｆ_N-3 )≡<N>Ｆ_N-3　(mod Ｆ_N)

Ｈ₄＝Ｆ_N-3×(<N>Ｆ_N-3 )−２≡２　(mod Ｆ_N)

Ｈ₅＝Ｆ_N-3×２−Ｆ_N-3≡Ｆ_N-3　(mod Ｆ_N)

＜補題６＞

G_N≡Ｆ_N-3(mod Ｆ_N)

∵　Ｆ_Nの漸化式を適用すると　

Ｆ_N+1+Ｆ_N-1＝２Ｆ_N＋Ｆ_N-3≡Ｆ_N-3(mod Ｆ_N)

＜補題７＞

Ｎが３の倍数でないとき　G_N　と　Ｆ_Nは奇数で互いに素

Ｎが３の倍数であるとき

GN ２

と

ＦN ２

は整数で互いに素

∵　Ｆ_Nの漸化式と互除法を逐次適用すると数学的帰納法により３ずつＮが低下して　、
G₃とＦ₃ or　G₂とＦ₂ or G₁とＦ₁になる。
このうち　G₃とＦ₃は４と２であるので最大公倍数は２である。
詳細略。

＜問題５証明＞

清川さんの補題等により　Ｆ_KNはＦ_Nの倍数であり、
Ｆ_MがＦ_Nの倍数であるためにはM＝KNでなければならない。

従って、Ｆ_N^２の倍数をＦ_Mに見つけるとき、M=KNが必要条件である。

すなわち、Ｆ_Mのうち、補題４に示される系列だけ調べればよい｡
またＦ_N　の倍数かどうかが問題であるので、全て(mod Ｆ_N)で考える｡　
以降　≡　は　(mod Ｆ_N)に限る。

補題４と補題６および補題１より

Ｆ_KN≡Ｆ_N-3Ｆ_N(K-1)−(<N>Ｆ_N(K-2))―――――（１）

Ｆ0＝０　、ＦN≡

αN−βN α−β

である。

（１）式は他にも別の初期値による系列がある。
（１）式は補題５の式と(mod Ｆ_N)　で同じであり、従ってそれは補題５のHそのものである。

さて、補題１より　α^N＝A　β^N＝B　と置くとき、

Ｆ_KN

＝	αKN−βKN α−β

＝

αN−βN α−β

×（AK-1＋AK-2B1＋AK‐3B2＋AK‐4B 3＋･･･A0B K-1）

AB=<N>1 を適用すると、

ＦKN ＦN

＝AK-1<N>AK-3＋AK‐5＋･･･項数K･･･<N> B K-３＋BK-1

＝(AK-1＋BK-1）<N>（AK-3＋BK-３）＋（AK‐5＋B K-5）<N>（AK-7＋B K-7） ･･･項数

［

K 2

+0.5］又は

［

K 2

］･･･ ±1または±(A+B) ―――（２）

補題４の形式の漸化式に立ち返り、解をもとめると　補題１のＦ_KNの解析式から
一般にX,Yを任意係数として　Xα^KN＋Yβ^KN　である。
よって、Hもこの形であり、初期条件から　X=Y=1である。
即ち，Ｈ_N、K＝α^KN＋β^KN＝A^K＋B^K　であり、
初期値条件　Ｈ_N、0＝２、
Ｈ_N、1＝α^N＋β^N＝G_N≡Ｆ_N-3 を満足している。

（２）式に適用すると

ＦKN ＦN

＝ＨN、K-1−ＨN、K-3＋ＨN、K-5−ＨN、K-7＋･･･±{１またはＨN、1}

(注　Ｈ_N、Iを使うと Iが２とびで符号を変えながら並んでいる状態である。
最後の±はその順で決まる。

具体的には<[

K-1 2

]>である。[ ]:ガウス記号)

(A)Ｋが奇数のときＫ−１は偶数だから補題５により、

０≡

ＦKN ＦN

≡<[

K-1 2

]>｛２＋２＋･･･+２＋１｝ ＝ <

K-1 2

>Ｋ

よって、０≡Ｋでなければならず、K＞0で最小のＫ＝Ｆ_N

(Ｂ)Ｋが偶数のとき補題５により、

０≡

ＦKN ＦN

≡<[

K-1 2

]>

ＫＨ1 ２

≡<

K 2

-1>

ＦN-3

Ｋ ２

補題７と補題６よりＦ_N-3はＦ_Nと高々２しか公約数を持たないので、

Ｋ ２

は

ＦN ２

の倍数でなければならない。

すなわち、K＞0で最小のＫ＝Ｆ_N

以上より最小のｍ＝ＮＦ_Nである。

【感想】

今回この問題を考えてみて、フィボナッチの世界にはその内部で結構構造を持っていることに驚きました。

この問題では

ＡK−ＢK Ａ−Ｂ

＝｛ K項(定数) の和　｝の線で

Ｋ＝Ｆ_Nが出るだろうと予想して考えました。
予想は当たりましたが、道は結構遠かったです。

今回使用しませんでしたが、その中で見つけた綺麗な関係として下記を問題として紹介します。

Ｆ_N+M+1＝Ｆ_N+1Ｆ_M+1＋Ｆ_NＦ_M
(Ｆ_2N+1＝Ｆ_N+1²＋Ｆ_N²)

◆広島県　清川　育男　さんからの解答。

【問題６】

【補題】

F(A+B)=F(A-1)*F(B)+F(A)*F(B+1)
証明は略。（度々使われています。）

　F(M+N+1)
=F((N+2)+(M-1))
=F(N+1)*F(M-1)+F(N+2)*F(M)
=F(N+1)*F(M-1)+(F(N+1)+F(N))*F(M)
=F(N+1)*(F(M-1)+F(M))+F(N)*F(M)
=F(N+1)*F(M+1)+F(N)*F(M)

M=Nのとき
F(2N+1)=F(N+1)²+F(N)²

◆兵庫県の高校生　そーうん　さんからの解答。

【問題３】

(予測して証明ではなく直接求める形にしました)
n＞4の時
a_n=a_n-1+a_n-2
　 =2a_n-2+a_n-3
　 =3a_n-3+a_n-4

よって
a_nが3の倍数のときa_n-4も3の倍数であり
a_n-4が3の倍数のときa_nも3の倍数である。・・・(1)

これを何度も適用すると
a_nはa₁,a₂,a₃,a₄のいずれかに帰着する。
ここでa₁=1 ,a₂=1 ,a₃=2 ,a₄=3

よって3の倍数はa₄に帰着するa_nのみだが、 そのようなｎは4の倍数のみである。
((1)より自明)

◆京都府　大空風成 さんからの解答。

【問題６】

Ｆ₁=1、Ｆ₂=1、Ｆ_N+Ｆ_N+1=Ｆ_N+2で
Ｆ_N+1Ｆ_M+1＋Ｆ_NＦ_M= Ｆ_N+M+1…(1)
を数学的帰納法によって証明する。

N=1のとき
（左辺）=Ｆ₂Ｆ_M+1+Ｆ₁Ｆ_M
　　　　 =Ｆ_M+1+Ｆ_M
　　　　 =Ｆ_M+2
　　　　 =Ｆ_1+M+1
　　　　 =(右辺)
よって、N=1のとき、(1)は成り立つ。

N=2のとき
Ｆ₃=Ｆ₁+Ｆ₂=1+1=2だから、
（左辺）=Ｆ₃Ｆ_M+1+Ｆ₂Ｆ_M
　　　　 =2Ｆ_M+1+Ｆ_M
　　　　 =Ｆ_M+1+Ｆ_M+1+Ｆ_M
　　　　 =Ｆ_M+1+Ｆ_M+2
　　　　 =Ｆ_M+3
　　　　 =Ｆ_2+M+1
　　　　 =(右辺)
よって、N=2のとき、(1)は成り立つ。

N=K、K+1のとき、(1)が成り立つと仮定すると、
Ｆ_K+1Ｆ_M+1＋Ｆ_KＦ_M=Ｆ_K+M+1
Ｆ_K+2Ｆ_M+1＋Ｆ_K+1Ｆ_M=Ｆ_K+M+2
となる。

N=K+2のとき
（左辺）=Ｆ_K+3Ｆ_M+1＋Ｆ_K+2Ｆ_M
　　　　 =(Ｆ_K+1+Ｆ_K+2)Ｆ_M+1＋(Ｆ_K+Ｆ_K+1)Ｆ _M
　　　　 =Ｆ_K+1Ｆ_M+1+Ｆ_K+2Ｆ_M+1＋Ｆ_KＦ _M+Ｆ_K+1Ｆ_M
　　　　 =(Ｆ_K+1Ｆ_M+1＋Ｆ_KＦ_M)+(Ｆ_K+2Ｆ _M+1+Ｆ_K+1Ｆ_M)
　　　　 =Ｆ_K+M+1+Ｆ_K+M+2
　　　　 =Ｆ_K+M+3
　　　　 =Ｆ_K+2+M+1
　　　　 =(右辺)
となり、N=K+2のときも(1)は成り立つ。

以上より、すべての自然数Nについて、(1)は成り立つ。

　『フィボナッチ数列の性質』へ

　数学の部屋へもどる