『殺人犯順列』解答

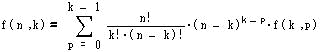
◆愛知県　Y.M.Ojisan さんからの解答。

【問題１】　n^n-1

【問題２】

	(n-1)!*nk
n-1Ｃk*nk=
	k!*(n-1-k)!

【証明】

f(1,0)=1　f(2,0)=1 f(2,1)=2 f(3,0)=1 f(3,1)=6 f(3,2)=9 であり　n＝３までは成立している。

ヒントにより
　

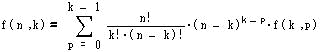
が証明できれば良い。右辺は変形すると
　

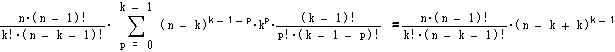
である。
n*(n-k+k)^k-1=n^k であるから　、
即ち　=f(n,k)である。

【ＰＳ】

殺人犯順列より家系図順列の方が穏当か。
グラフ理論では　ラベル付き木（問題１）ないし森（問題２）と呼ぶようで、この問題は「Cayleyの定理」の応用と考えられます。
http://ocw.hokudai.ac.jp/Course/Faculty/Engineering/GraphTheory/2005/page/materials/GraphTheory-2005-Slide-07.pdf

◆出題者のコメント。

Y.M.Ojisanさん、解答ありがとうございます。

出題から１ヶ月も解答がなかったので、とても嬉しいです。
ただ、答は正しいですが、やや証明が不十分では。

Ｆ(ｋ,ｐ) をｋp*

(k-1)! P!(k-1-p)!

すなわち _k-1Ｃ_p*ｋ^p といきなり変形していますが、 これでは証明すべきこと証明なしで利用していることになります。

Ｆ(ｋ,ｐ)＝_k-1Ｃ_p*ｋ^p といきなりできるなら、
Ｆ(n,k)＝_n-1Ｃ_k*n^kは自明で証明は不要です。

ヒントでも書いたように、漸化式に従って順次求めていけば
予想式 F(n,k)=_n-1Ｃ_k*n^kは見えますから、この問題で大事なのはその予想式の証明です。

出題者としても、どのような「証明」が寄せられるか楽しみにしているわけです。

お手数ですが、「どのようにして右辺からＦ(ｋ,p)が消せたのか？」を、(１行だけでなく)もう少し噛み砕いて説明をして頂けないでしょうか。

【ＰＳ】

問題の設定がシンプルで済むため『殺人犯順列』にしましたが、あまり良い命名でないのは承知しています。
実在したｎ人の女(男)性の「名前の集合」を考えたとき、その集合内での『母(父)親順列』なら同じ問題ですが、設定がシンプルでないのを嫌って本問にした次第です。

この問題は、私が数年前に考案した『５つのナップザック』問題を掘り起こして生まれたものです。
「もっと上手い証明がないだろうか」と考えている内に、この問題が生まれました。

◆愛知県　Y.M.Ojisan さんからの解答。

【補足】

上記　f(k,p)を代入し変形後の式の　Σの中身は、
(A+B)^k-1　｛ここで　A=n-k B=k｝　の２項展開式そのものである。

従って Σの値＝n^k-1 である。

でいかがでしょうか。

　『殺人犯順列』へ

　数学の部屋へもどる