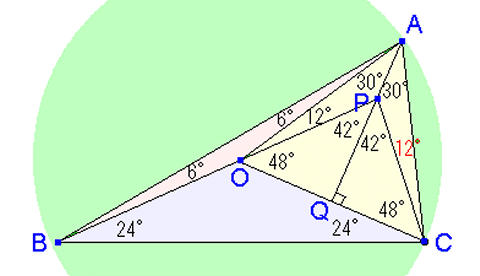
◆山梨県 Footmark さんからの解答。
[答え] 12°
「百聞は一見にしかず」下の図を見てください。

三角形OABと三角形OBCは二等辺三角形、
三角形OCAは正三角形。
また、線分AQは線分OCに垂直に接する。
◆愛知県 Y.M.Ojisan さんからの解答。
【解答】 12度
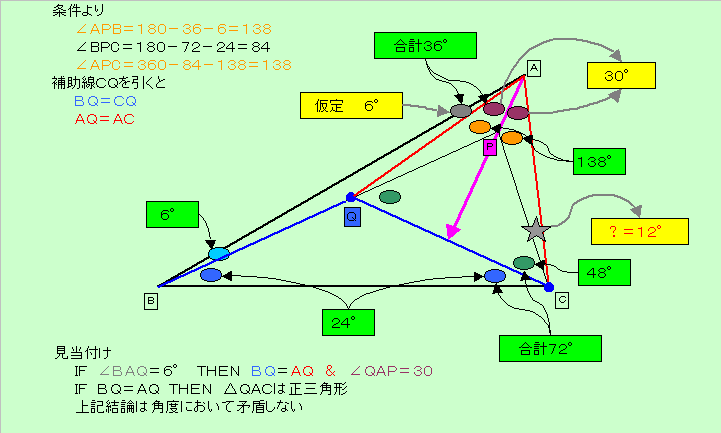
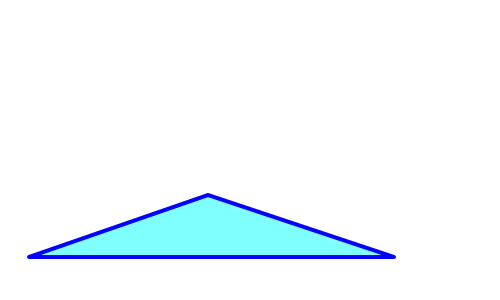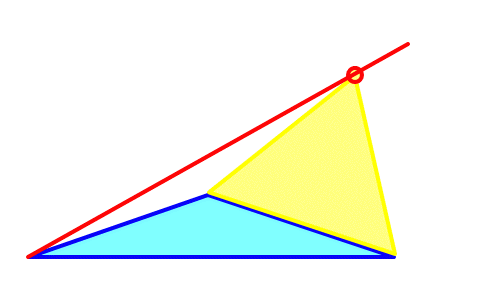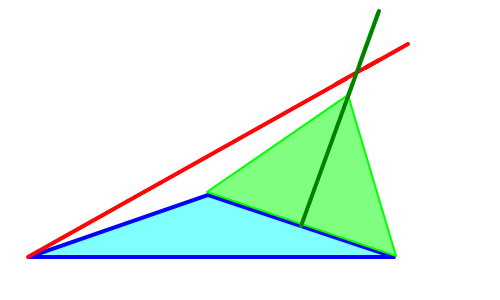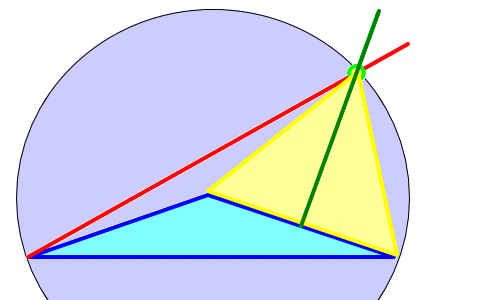
点P周りの角のうち2つが138度であることを利用して補助線CQを引くと、下図より、少なくとも12度という解が存在する。
なお図中、緑枠内数値は条件から直接得られる値で、
黄色枠は∠BAQ=6度の仮定から得られる値。
また、線分BPから始める作図の方法を考慮すれば、図形が1種類だけであることは明白。
よって、見当をつけた解のみである。
【感想】
初等的といわれるとかえって困ってしまいますね。
この方法は当て物みたいで、期待された解答としていいのか悪いのか不安です。
【出題者のコメント】
答えは正解なのですが、何故三角形ABCの外心がPB上にあるかを示せないと正解とは言えないと思います。
両者とも三角形ABCの外心をOとすると、三角形OCAが正三角形ということを使われています。
私もこれはわかっていたのですが、OがPB上にあるということを示すことができませんでした。
◆愛知県 Y.M.Ojisan さんからのコメント。
【RE:コメント】
Q[O]が△ABCの外心であるという条件は使っておりません。
●図に表したつもりでしたが、若干説明不足でしたので補足説明いたします。
まず、点QはCを通りAPに垂直な線とPBとの交点です。
このように引くと直接∠QCB=24°が計算されるので、
QB=QCが得られます。
また、直接∠APC=∠APQ[B]=138度が計算されるので、
△AQCはAPを対称線として中身が対称な
AQ=ACの二等辺三角形です。
ここで∠BAQ=6°を仮定すると QB=QAになります。
従って、△AQCは正三角形です。
かつAPは対称線ですから、∠PAQ=30°です。
それら結果合計と ∠BAP=36°とは矛盾していません。
即ち解答の少なくとも一つです。
●以上は私が見つけた道順を示したものですが,Q[O]を△ABCの外心として「仮定して」始めても同様です。
この場合は∠BAQ=6°でなければならず、△AQCは正三角形です。
あとは、線分APが角Aの2等分線であれば良い。
これは、角度を計算すると直接
∠PCQ=∠PQC=48°が得られるので点Pは対称中心線上にあることが分かるので証明されます。
いろいろ道順はありますが、結局、FOOTMARKさんの示された図形が見つけられれば、途中はどうでも良くて、与えられた条件を満足しているので解の一つです。
●あとは解の唯一性ですが、これは問題の作図から明白です。
従って、ある意味でたまたま見つけたものが唯一解となります。
●なお、∠ABQ=∠BAQ=6°
∠ABQ+∠BAQ=12°=∠AQPですから、
BQPは一直線上です。
◆山梨県 Footmark さんからのコメント。
条件を満たす具体的な図に何の矛盾もなければ1つの幾何学的解答だと思いますが、その件はさておいて取り敢えず解答を発見するまでの解法を示します。
以下、解法です。
[解法]
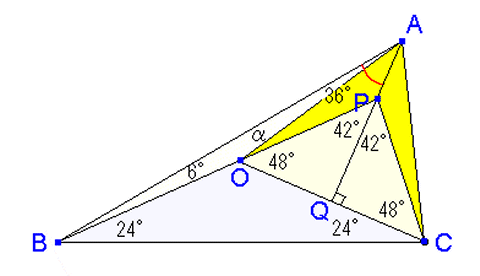
与えられた条件から、上の図までは容易に判明します。
(ただし、点Oは△ABCの外心とは限らない。)
線分AQは線分OCの垂直二等分線上にあることも分かります。
ですから、△POAと△PCAは合同です。
そこで、∠BAO=α とします。
点Oが△ABCの外心であると仮定すると
(1): ∠OAB=∠OBA
(2): ∠OBC=∠OCB
(3): ∠OCA=∠OAC
いずれも成立しなければなりません。
α は与えられた角度ではないので、3つとも同時に成立する α があれば逆に点Oは外心の筈です。
それぞれを具体的に当てはめてみると、
(1):α =6°
(2):24°=24°
△POAと△PCAが合同であることを利用して
(3):48°+(6°+α)=2(36°ーα)
∴ α =6°
成立する α=6°がありましたから、点Oは△ABCの外心です。
逆に言えば、与えられた条件では
「点Oは△ABCの外心」で「∠BAO=6°」になります。
△POAと△PCAは合同ですから、
∠PCA=∠POA=12°
[P・S]
点Oが△ABCの外心であることを発見すれば、△AOCが正三角形であることは特に利用する必要はありません。
結果として、△AOCが正三角形になっただけです。
◆宮城県 アンパンマン さんからのコメント。
この問題もっと一般的な場合に拡張するとこうなります。
∠ABP=x
∠PBC=30-x
∠PCB=90-3x
∠PAB=30+x
このとき∠PCAの大きさを求めなさい。
もちろん、答えは2xです。
【出題者のコメント】
Y.M.OjisanさんもFootmarkさんも確かに三角形OBCが正三角形という性質は利用されていませんね。
これは失礼しました。
ただ証明手法がどちらも間接的手法なので、個人的には何かすっきりしていません。
PB上にOをとって三角形OBCが正三角形とすることができることを直接的に示せないでしょうか?。
出題者はこれを示すことができないでいるんですが。
私が持っている解法は別の手法を用いています。
PS.アンパンマンさんの拡張には気づきませんでした。
◆愛知県 Y.M.Ojisan さんからの解答。
【解答#2】
基本的には変わっていないのですが、出題者のすっきりしない部分を70%ぐらいは解消できそうな解釈をつけましたのでご覧下さい。
◆宮城県 アンパンマン さんからの解答。
【解答】
この問題はもともとOA=OB=OCとBPは点Oを通ることと
∠PCAが簡単に求まるような∠OAPという条件を満たすときに、
∠PCAが求まるという事を利用します。
さらに∠COAが60°のとき△OACが正三角形になることを利用して
OA=OCの条件をOA=ACに変えます。
この二つの重なり(Oは△ABCの外接円の中心と∠COA=60°)で奇跡が起こり、証明も困難になってしまいます。
そのため、OA=OCを証明できれば∠PCAも簡単に求められます。

【証明】
説明を省くために、Footmark さんによる結果を利用します。
その結果とは線分AQは線分OCの垂直二等分線上にあること
(つまりAO=AC)とBO=OCです。
次はOA=OCを証明します。
まず、正三角形ODCを作ります。
APDは一直線上です。
∠BCD=60−∠BCO=30+x=∠BADより、点Dは△ABCの外接円上にあることがわかります。
OB=OC=ODとB、C、Dが違う点になることより、点Oは□ABCDの外接円の中心になります。
ゆえにOA=OCです。
∠OBA=∠OAB=xで、
∠ACP=∠AOP=∠OBA+∠OAB=2xです。
DとBが同じ点になる場合(x=−30)も、
Limitの考えで∠ACP=−60です。
◆静岡県 村松 芳子 さんからの解答。
PB上にDをとり、∠PAD=30°とする。
PC上にEをとり、∠PAE=30°とする。
∠APB=∠APC=138°、APは共通だから、
△ADP≡△ADE
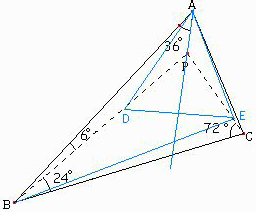
ゆえに AD=AE
∠DAE=60°
ゆえに △ADEは正三角形である。
また、∠DAB=∠DBA=6°だから、AD=DB
したがって AD=DB=DEとなり、Dは△ABEの外心である。
∠ABEは円周角、∠ADEは中心角の関係から、
∠ABE=60°/2=30°となる。
もとより∠ABC=30°だからBEとBCは同一直線ということになり、EはCに一致する。
ゆえに、∠ACP=∠AEP=12°である。