◆宮城県 アンパンマン さんからのコメント。
この問題を拡張するとこうなります。
∠ABP=x
∠PBC=30-x
∠PCB=90-3x
∠PAB=30+x
ただし点Pは△ABCの外側にあります。
(xが負のとき、点Pが線ACの右側に移ります)
このとき∠PCAの大きさを求めなさい。
答えは4xです。
◆山梨県 Footmark さんからの解答。

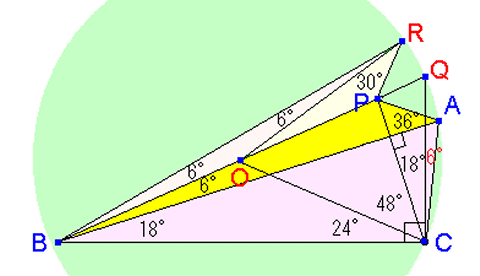
『角度の問題 Part5』より、図で△RBCの外心は点Oです。
線分BPの延長線と△RBCの外接円との交点をQとします。
線分BQは明らかにその外接円の直径です。
点Aは直径BQに対して点Rの対称点にあたります。
ですから、点Aもその外接円の円周上にある筈です。
∠BCQは明らかに 90°ですから、
∠PCQ=90°ー72°=18°
∠QCAは弦QAの張る円周角で∠QBAと等しく 6°
よって、求める角度の、∠PCAは
∠PCA=∠PCQ+∠QCA=18°+6°=24°
[答え] 24°
◆出題者のコメント。
『角度の問題 Part5』の解答をベースにして良いわけですから、アンパンマンさんのコメントは解答と言ってよいでしょう。
正三角形ベース+円周角の性質等から導出されているのであろうと思いますが、是非解説をお願いいたします。
◆宮城県 アンパンマン さんからの解答。
『角度の問題 Part5』問題より、
点Oは□EBCDの外接円の中心です。
線BOによる点Eの対称になる点Aは□EBCDの外接円上にあり、
∠ABR=∠EBR=xです。
∠ECA=∠ABR+∠EBR=2xと『角度の問題 Part5』問題より
∠PCE=2xで、
∠PCA=∠ECA+∠PCE=2x+2x=4xです。
◆神奈川 クラテス さんからの解答。
『角度の問題 Part5』の解法を利用して解いてみました。
非常に回りくどいですが、直接的に証明できています。
これを参考に『角度の問題 Part5』の直接的な解法をいただければ幸いです。
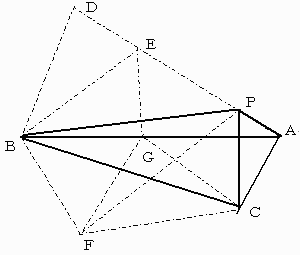
APを延長して、AB=ADとなるDをとる。
この時∠ABD=∠ADB=72°である。
次にAD上にBD=BEとなるEを、
AB上にBE=BGとなるGをとる。
この時、∠BDE=∠BED=∠BEG=∠BGE=72°となり、
△BDE≡△BEGとなるから、DE=EGである。
また∠GEA=∠GAE=36°よりEG=GAである。
次にBPに関してDを折り返した点をFとする。
BD=BFであり、かつ
∠GBF
=∠PBF−∠PBA
=∠PBD−∠PBA
=66°―6°
=60°
よって△BFGは正三角形である。
したがって、BD=BE=BG=BF=FGである。
∠BPF=∠BPD=∠PBA+∠PAB=42°より、
∠FPC=∠BPC−∠BPF=84°−42°=42°
一方、∠FBC=∠FBG−∠CBA=60°―18°=42°だから、
結局∠FBC=∠FPCとなり、4点P,B,F,Cは同一円周上の点となる。
∠FBC=∠FCB=∠BPF=42°となるから、
△FBCは二等辺三角形であり、FB=FCである。
Fを中心に半径BFの円において、
| ∠BCG= | 1 2 | ∠BFGとなるから、∠BCG=30° |
FG=FCであるから、∠FGC=∠FCG=72°
よって、△BDE,△BEG、△FCGはいずれも合同な二等辺三角形となる。
よって、DE=EG=GCである。
よって、GA=GCとなり、三角形GACは二等辺三角形。
∠AGC
=180°―∠FGC−∠BGF
=180°―72°―60°
=48°
よって、∠GAC=66°となり、∠PCAは結局24°となる。
【コメント】
回りくどいですが、直接的に示せました。
この手法は『角度の問題 Part5』の解法より難しいのですが、同じようにして『角度の問題 Part5』も示すことができます。
◆出題者のコメント。
これはすごい。
100年たっても私には見つけられないでしょう。